队列

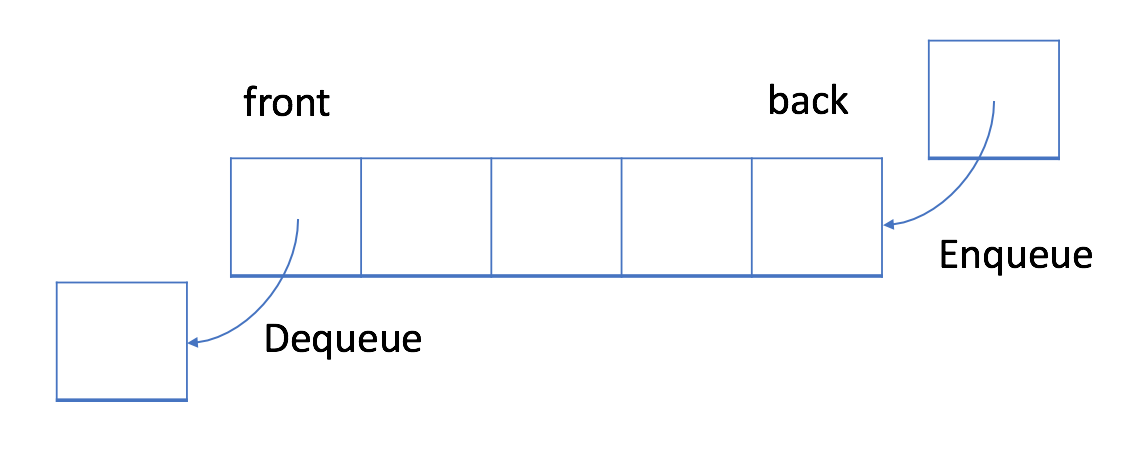
在 FIFO 数据结构中，将首先处理添加到队列中的第一个元素。

如上图所示，队列是典型的 FIFO 数据结构。

插入（insert）操作也称作入队（enqueue），新元素始终被添加在队列的末尾。
删除（delete）操作也被称为出队（dequeue)，你只能移除第一个元素。

队列可以应用在任何有限资源池中，用于排队请求，比如数据库连接池等。实际上，对于大部分资源有限的场景，当没有空闲资源时，基本上都可以通过“队列”这种数据结构来实现请求排队。

简单实现

为了实现队列，可以使用动态数组和指向队列头部的索引。

如上所述，队列应支持两种操作：入队和出队。入队会向队列追加一个新元素，而出队会删除第一个元素。所以需要一个索引来指出起点。

这是一个仅供参考的实现：

#include <iostream>
class MyQueue {
    private:
        // store elements
        vector<int> data;       
        // a pointer to indicate the start position
        int p_start;            
    public:
        MyQueue() {p_start = 0;}
        /** Insert an element into the queue. Return true if the operation is successful. */
        bool enQueue(int x) {
            data.push_back(x);
            return true;
        }
        /** Delete an element from the queue. Return true if the operation is successful. */
        bool deQueue() {
            if (isEmpty()) {
                return false;
            }
            p_start++;
            return true;
        };
        /** Get the front item from the queue. */
        int Front() {
            return data[p_start];
        };
        /** Checks whether the queue is empty or not. */
        bool isEmpty()  {
            return p_start >= data.size();
        }
};
int main() {
    MyQueue q;
    q.enQueue(5);
    q.enQueue(3);
    if (!q.isEmpty()) {
        cout << q.Front() << endl;
    }
    q.deQueue();
    if (!q.isEmpty()) {
        cout << q.Front() << endl;
    }
    q.deQueue();
    if (!q.isEmpty()) {
        cout << q.Front() << endl;
    }
}

缺点:

随着起始指针的移动，浪费了越来越多的空间。当我们有空间限制时，这将是难以接受的。

循环队列

更有效的方法是使用 循环队列。具体来说，我们可以使用 固定大小的数组 和 两个指针 来指示起始位置和结束位置。目的是重用我们之前提到的被浪费的存储。

方案一

class MyCircularQueue:
  def __init__(self, k: int):
      """
      Initialize your data structure here. Set the size of the queue to be k.
      """
      self._size = k
      self._queue = [None] * k
      self._head = 0 # 指向当前头指针位置
      self._tail = 0 # 指向下一个要插入元素的位置
      self._is_full = False
  def enQueue(self, value: int) -> bool:
      """
      Insert an element into the circular queue. Return true if the operation is successful.
      """
      if self.isFull():
          return False
      self._queue[self._tail] = value
      self._tail += 1
      if self._tail == self._size:
          self._tail = 0
      if self._head == self._tail:  # 尾指针追上头指针
          self._is_full = True
      return True
  def deQueue(self) -> bool:
      """
      Delete an element from the circular queue. Return true if the operation is successful.
      """
      if self.isEmpty():
          return False
      # 出队操作
      # value = self._queue[self._head]
      self._is_full = False
      self._head += 1
      if self._head == self._size:
          self._head = 0
      return True
  def Front(self) -> int:
      """
      Get the front item from the queue.
      """
      if self.isEmpty():
          return -1
      return self._queue[self._head]
  def Rear(self) -> int:
      """
      Get the last item from the queue.
      """
      if self.isEmpty():
          return -1
      return self._queue[self._tail - 1]
  def isEmpty(self) -> bool:
      """
      Checks whether the circular queue is empty or not.
      """
      if self._head == self._tail and not self._is_full:
          return True
      return False
  def isFull(self) -> bool:
      """
      Checks whether the circular queue is full or not.
      """
      return self._is_full

方案二

class MyCircularQueue:

  def __init__(self, k: int):
      """
      Initialize your data structure here. Set the size of the queue to be k.
      """
      self._size = k
      self._queue = [None] * k
      self._head = 0 # 指向当前头指针位置
      # self._tail = 0 # 指向下一个要插入元素的位置，可以通过 (self._num + self._head) % self._size 计算出来
      self._num = 0 # 当前元素的数量

  def enQueue(self, value: int) -> bool:
      """
      Insert an element into the circular queue. Return true if the operation is successful.
      """
      if self.isFull():
          return False
      self._queue[(self._num + self._head) % self._size] = value
      self._num += 1

      return True

  def deQueue(self) -> bool:
      """
      Delete an element from the circular queue. Return true if the operation is successful.
      """
      if self.isEmpty():
          return False
      # 出队操作
      # value = self._queue[self._head]
      self._num -= 1
      self._head += 1
      if self._head == self._size:
          self._head = 0
      return True

  def Front(self) -> int:
      """
      Get the front item from the queue.
      """
      if self.isEmpty():
          return -1

      return self._queue[self._head]

  def Rear(self) -> int:
      """
      Get the last item from the queue.
      """
      if self.isEmpty():
          return -1

      return self._queue[(self._num + self._head) % self._size - 1]

  def isEmpty(self) -> bool:
      """
      Checks whether the circular queue is empty or not.
      """
      return self._num == 0

  def isFull(self) -> bool:
      """
      Checks whether the circular queue is full or not.
      """
      return self._num == self._size

leetcode测试结果, 性能而言, 此方案比上一个方案好很多

官方提供的参考方案

class MyCircularQueue {
private:
  vector<int> data;
  int head;
  int tail;
  int size;
public:
  /** Initialize your data structure here. Set the size of the queue to be k. */
  MyCircularQueue(int k) {
      data.resize(k);
      head = -1;
      tail = -1;
      size = k;
  }

  /** Insert an element into the circular queue. Return true if the operation is successful. */
  bool enQueue(int value) {
      if (isFull()) {
          return false;
      }
      if (isEmpty()) { // 这一步, 减少了很多其他过程中的判断
          head = 0;
      }
      tail = (tail + 1) % size;
      data[tail] = value;
      return true;
  }

  /** Delete an element from the circular queue. Return true if the operation is successful. */
  bool deQueue() {
      if (isEmpty()) {
          return false;
      }
      if (head == tail) { // 减少了判断是否为空的条件
          head = -1;
          tail = -1;
          return true;
      }
      head = (head + 1) % size;
      return true;
  }

  /** Get the front item from the queue. */
  int Front() {
      if (isEmpty()) {
          return -1;
      }
      return data[head];
  }

  /** Get the last item from the queue. */
  int Rear() {
      if (isEmpty()) {
          return -1;
      }
      return data[tail];
  }

  /** Checks whether the circular queue is empty or not. */
  bool isEmpty() {
      return head == -1;
  }

  /** Checks whether the circular queue is full or not. */
  bool isFull() { // 循环队列应该尾指针追上头指针才为满
      return ((tail + 1) % size) == head;
  }
};

个人认为方案二最佳, 方案三采用的一些操作很有效的去掉了方案一种特殊情况的判断, 值得思考

阻塞队列和并发队列

阻塞队列其实就是在队列基础上增加了阻塞操作。

简单来说，就是在队列为空的时候，从队头取数据会被阻塞。因为此时还没有数据可取，直到队列中有了数据才能返回；如果队列已经满了，那么插入数据的操作就会被阻塞，直到队列中有空闲位置后再插入数据，然后再返回。

go channel?

线程安全的队列我们叫作并发队列。最简单直接的实现方式是直接在 enqueue()、dequeue() 方法上加锁，但是锁粒度大并发度会比较低，同一时刻仅允许一个存或者取操作。

实际上，基于数组的循环队列，利用 CAS 原子操作，可以实现非常高效的并发队列。这也是循环队列比链式队列应用更加广泛的原因。

广度优先搜索（BFS）

算法模板

/**
 * Return the length of the shortest path between root and target node.
 */
int BFS(Node root, Node target) {
    Queue<Node> queue;  // store all nodes which are waiting to be processed
    int step = 0;       // number of steps neeeded from root to current node
    // initialize
    add root to queue;
    // BFS
    while (queue is not empty) {
        step = step + 1;
        // iterate the nodes which are already in the queue
        int size = queue.size();
        for (int i = 0; i < size; ++i) {
            Node cur = the first node in queue;
            return step if cur is target;
            for (Node next : the neighbors of cur) {
                add next to queue;
            }
            remove the first node from queue;
        }
    }
    return -1;          // there is no path from root to target
}

在每一轮中，队列中的结点是等待处理的结点。
在每个更外一层的 while 循环之后，我们距离根结点更远一步。变量 step 指示从根结点到我们正在访问的当前结点的距离。

无法知道最短路径，仅能找到最短路径的长度。

有时，确保我们永远不会访问一个结点两次很重要。否则，我们可能陷入无限循环。如果是这样，我们可以在上面的代码中添加一个哈希集来解决这个问题。

有两种情况你不需要使用哈希集：

确定没有循环，例如，在树遍历中；
确实希望多次将结点添加到队列中。
栈
与队列不同，栈是一个 LIFO 数据结构。通常，插入操作在栈中被称作入栈 push。与队列类似，总是 在堆栈的末尾添加一个新元素。但是，删除操作，退栈 pop ，将始终删除队列中相对于它的最后一个元素。

实际上，栈既可以用数组来实现，也可以用链表来实现。用数组实现的栈，叫作顺序栈，用链表实现的栈，叫作链式栈。

深度优先搜索

深度优先搜索（DFS）是用于在 树/图中遍历/搜索 的另一种重要算法。

我们可以用 DFS 进行前序遍历，中序遍历和后序遍历。在这三个遍历顺序中有一个共同的特性：除非我们到达最深的结点，否则我们永远不会回溯。

DFS 和 BFS 之间最大的区别，BFS永远不会深入探索，除非它已经在当前层级访问了所有结点。

通常，我们使用递归实现 DFS。

DFS - 模板 I

在大多数情况下，在能使用 BFS 时也可以使用 DFS。但是有一个重要的区别：遍历顺序。

与 BFS 不同，更早访问的结点可能不是更靠近根结点的结点。因此，你在 DFS 中找到的第一条路径可能不是最短路径。

递归方式

/*
 * Return true if there is a path from cur to target.
 */
boolean DFS(Node cur, Node target, Set<Node> visited) {
    return true if cur is target;
    for (next: each neighbor of cur) {
        if (next is not in visited) {
            add next to visted;
            return true if DFS(next, target, visited) == true;
        }
    }
    return false;
}

当我们递归地实现 DFS 时，似乎不需要使用任何栈。但实际上，我们使用的是由系统提供的隐式栈，也称为调用栈（Call Stack）。

每个元素都需要固定的空间。栈的大小正好是 DFS 的深度。因此，在最坏的情况下，维护系统栈需要队列&栈 - 图2 ，其中 h 是 DFS 的最大深度。在计算空间复杂度时，永远不要忘记考虑系统栈。

DFS - 模板 II

递归解决方案的优点是它更容易实现。但是，存在一个很大的缺点：如果递归的深度太高，你将遭受堆栈溢出。在这种情况下，可能会希望使用 BFS，或使用显式栈实现 DFS。

这里提供了一个使用显式栈的模板：

/*
 * Return true if there is a path from cur to target.
 */
boolean DFS(int root, int target) {
    Set<Node> visited;
    Stack<Node> s;
    add root to s;
    while (s is not empty) {
        Node cur = the top element in s;
        return true if cur is target;
        for (Node next : the neighbors of cur) {
            if (next is not in visited) {
                add next to s;
                add next to visited;
            }
        }
        remove cur from s;
    }
    return false;
}

该逻辑与递归解决方案完全相同。但使用 while 循环和栈来模拟递归期间的系统调用栈。

参考链接

https://leetcode-cn.com/explore/learn/card/queue-stack/216/queue-first-in-first-out-data-structure/862/
https://leetcode-cn.com/explore/learn/card/queue-stack/216/queue-first-in-first-out-data-structure/863/
https://leetcode-cn.com/explore/learn/card/queue-stack/216/queue-first-in-first-out-data-structure/864/
https://leetcode-cn.com/explore/learn/card/queue-stack/216/queue-first-in-first-out-data-structure/865/
https://leetcode-cn.com/explore/learn/card/queue-stack/217/queue-and-bfs/870/
https://leetcode-cn.com/explore/learn/card/queue-stack/219/stack-and-dfs/
https://leetcode-cn.com/explore/learn/card/queue-stack/219/stack-and-dfs/882/
https://time.geekbang.org/column/article/41222?utm_term=pc_interstitial_235
https://time.geekbang.org/column/article/41330?utm_term=pc_interstitial_235