树的基本概念
- 节点的高度:节点到叶子节点的最长路径(边数)
- 节点的深度:根节点到这个节点所经历的边的个数
- 节点的层数:节点的深度+1
- 树的高度:根节点的高度
特殊的二叉树
- 满二叉树:除了叶子节点,每个节点都有左右两个子结点的树;
- 完全二叉树:除了最后一层,其他层的节点数都达到最大,并且最后一层子结点都靠左排列。
树的存储
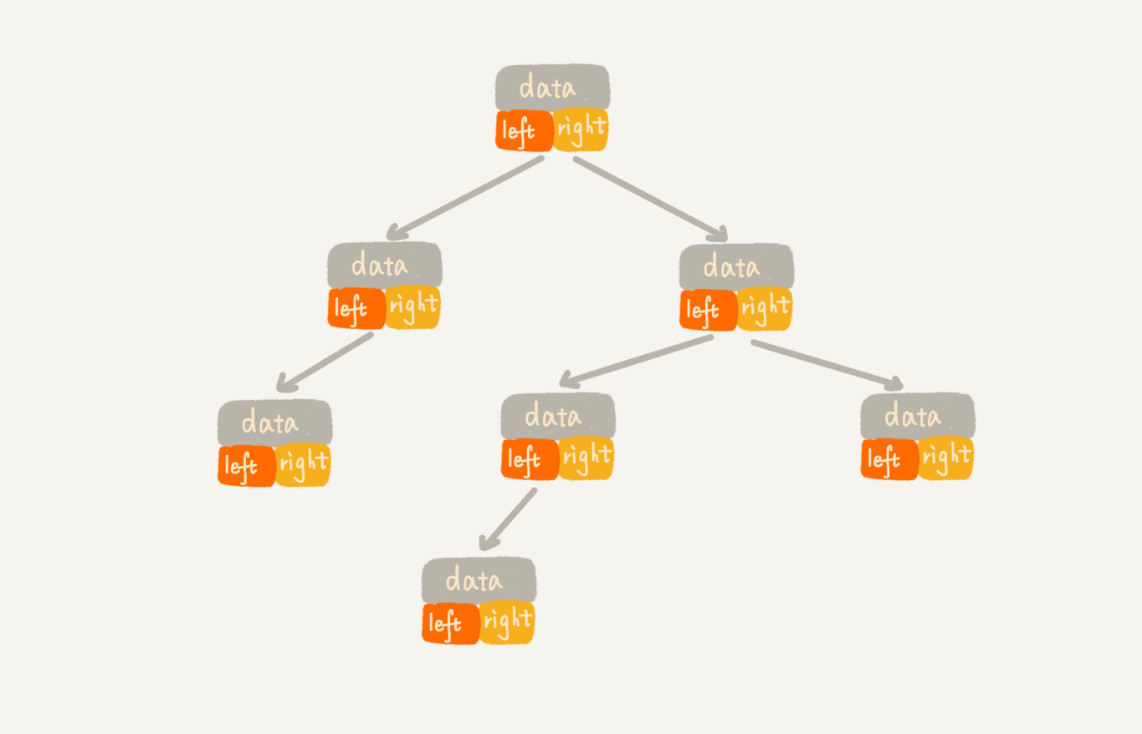
链式存储
顺序存储
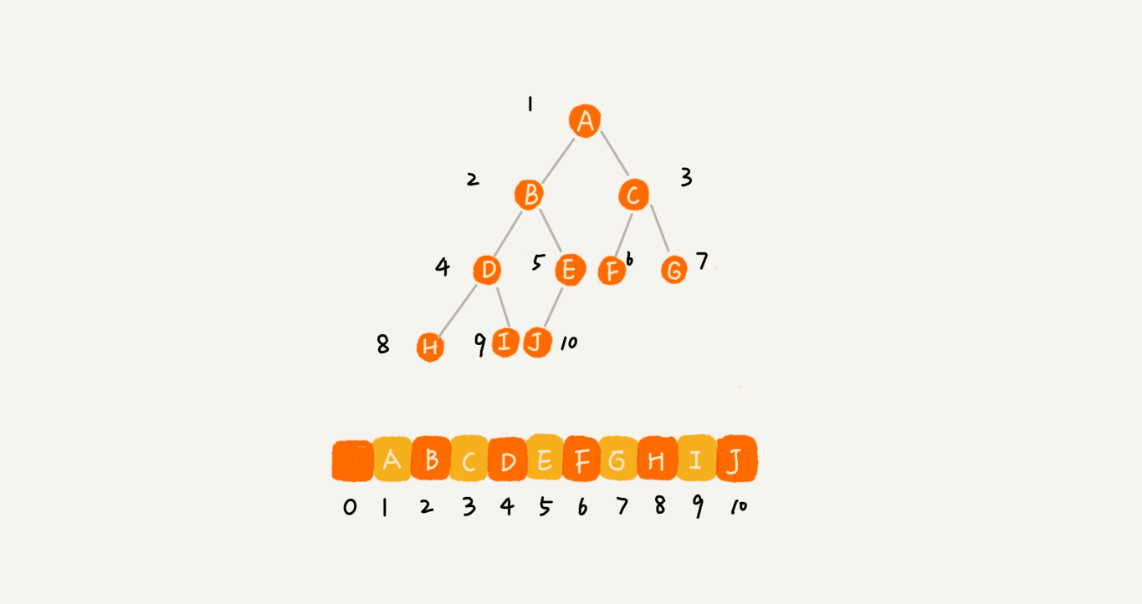
如果节点 X 存储在数组中下标为 i 的位置,下标为 2 i 的位置存储的就是左子节点,下标为 2 i + 1 的位置存储的就是右子节点。反过来,下标为 i/2 的位置存储就是它的父节点。通过这种方式,我们只要知道根节点存储的位置(一般情况下,为了方便计算子节点,根节点会存储在下标为 1 的位置),这样就可以通过下标计算,把整棵树都串起来。
完全二叉树适合使用数组来存储,堆就是其一个常见用途。**
树的遍历
- 前序遍历——递归
- 中序遍历——递归
- 后序遍历——递归
- 层序遍历——广度有限搜索
前序遍历
前序遍历首先访问根节点,然后遍历左子树,最后遍历右子树。中序遍历
中序遍历是先遍历左子树,然后访问根节点,然后遍历右子树。后序遍历
后序遍历是先遍历左子树,然后遍历右子树,最后访问树的根节点。层序遍历
层序遍历就是逐层遍历树结构。
广度优先搜索 是一种广泛运用在树或图这类数据结构中,遍历或搜索的算法。
运用递归解决树的问题
树可以以递归的方式定义为一个节点(根节点),它包括一个值和一个指向其他节点指针的列表。 递归是树的特性之一。 因此,许多树问题可以通过递归的方式来解决。 对于每个递归层级,我们只能关注单个节点内的问题,并通过递归调用函数来解决其子节点问题。
“自顶向下” 的解决方案
“自顶向下” 意味着在每个递归层级,我们将首先访问节点来计算一些值,并在递归调用函数时将这些值传递到子节点。所以 “自顶向下” 的解决方案可以被认为是一种 前序遍历。
具体来说,递归函数 top_down(root, params) 的原理是这样的:
1. return specific value for null node2. update the answer if needed // anwer <-- params3. left_ans = top_down(root.left, left_params) // left_params <-- root.val, params4. right_ans = top_down(root.right, right_params) // right_params <-- root.val, params5. return the answer if needed // answer <-- left_ans, right_ans
示例:给定一个二叉树,请寻找它的最大深度。
private int answer; // don't forget to initialize answer before call maximum_depth
private void maximum_depth(TreeNode root, int depth) {
if (root == null) {
return;
}
if (root.left == null && root.right == null) {
answer = Math.max(answer, depth);
}
maximum_depth(root.left, depth + 1);
maximum_depth(root.right, depth + 1);
}
“自底向上” 的解决方案
“自底向上” 是另一种递归方法。 在每个递归层次上,我们首先对所有子节点递归地调用函数,然后根据返回值和根节点本身的值得到答案。 这个过程可以看作是 后序遍历 的一种。
通常, “自底向上” 的递归函数 bottom_up(root) 为如下所示:
1. return specific value for null node
2. left_ans = bottom_up(root.left) // call function recursively for left child
3. right_ans = bottom_up(root.right) // call function recursively for right child
4. return answers // answer <-- left_ans, right_ans, root.val
示例:对于树的单个节点,以节点自身为根的子树的最大深度 x 是多少?
如果我们知道一个根节点,以其左子节点为根的最大深度为l和以其右子节点为根的最大深度为r,我们是否可以回答前面的问题?
当然可以,我们可以选择它们之间的最大值,再加上 1 来获得根节点所在的子树的最大深度。那就是 x = max(l,r)+ 1。
public int maximum_depth(TreeNode root) {
if (root == null) {
return 0; // return 0 for null node
}
int left_depth = maximum_depth(root.left);
int right_depth = maximum_depth(root.right);
return Math.max(left_depth, right_depth) + 1; // return depth of the subtree rooted at root
}
总结
当遇到树问题时,请先思考一下两个问题:
- 你能确定一些参数,从该节点自身解决出发寻找答案吗?
- 你可以使用这些参数和节点本身的值来决定什么应该是传递给它子节点的参数吗?
如果答案都是肯定的,那么请尝试使用 自顶向下 的递归来解决此问题。
或者可以这样思考:
对于树中的任意一个节点,如果你知道它子节点的答案,你能计算出该节点的答案吗?
如果答案是肯定的,那么 自底向上 的递归可能是一个不错的解决方法。
参考链接
https://leetcode-cn.com/explore/learn/card/data-structure-binary-tree/2/traverse-a-tree/7/
https://leetcode-cn.com/explore/learn/card/data-structure-binary-tree/3/solve-problems-recursively/11/
https://time.geekbang.org/column/article/67856