定义

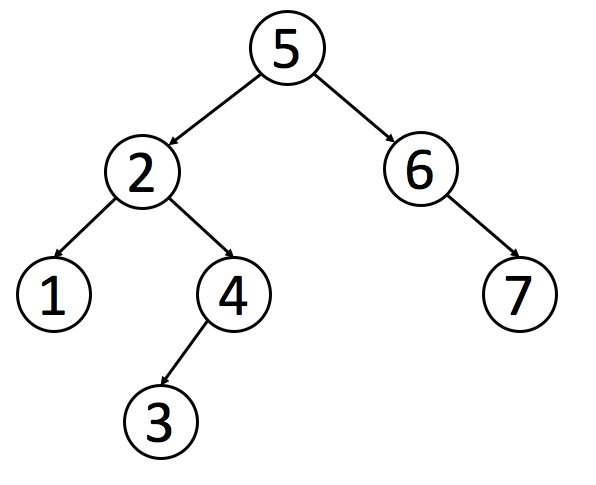
二叉搜索树是二叉树的一种特殊形式。

二叉搜索树具有以下性质：

1. 每个节点中的值必须大于（或等于）其左侧子树中的任何值
2. 小于（或等于）其右侧子树中的任何值。

对于二叉搜索树，可以通过 中序遍历 得到一个 递增的有序序列。因此，中序遍历是二叉搜索树中最常用的遍历方法。

基本操作

搜索

根据BST的特性，对于每个节点：

1. 如果目标值等于节点的值，则返回节点;
2. 如果目标值小于节点的值，则继续在左子树中搜索;
3. 如果目标值大于节点的值，则继续在右子树中搜索。

   插入

有许多不同的方法去插入新节点，这篇文章中，我们只讨论一种使整体操作变化最小的经典方法。

它的主要思想是 为目标节点找出合适的叶节点位置，然后将该节点作为叶节点插入。 因此，搜索将成为插入的起始。

与搜索操作类似，对于每个节点，我们将：

1. 根据节点值与目标节点值的关系，搜索左子树或右子树；
2. 重复步骤 1 直到到达外部节点；
3. 根据节点的值与目标节点的值的关系，将新节点添加为其左侧或右侧的子节点。

   删除

删除要比我们前面提到过的两种操作复杂许多。有许多不同的删除节点的方法，这篇文章中，我们只讨论一种使整体操作变化最小的方法。

我们的方案是 用一个合适的子节点来替换要删除的目标节点。根据其子节点的个数，我们需考虑以下三种情况：

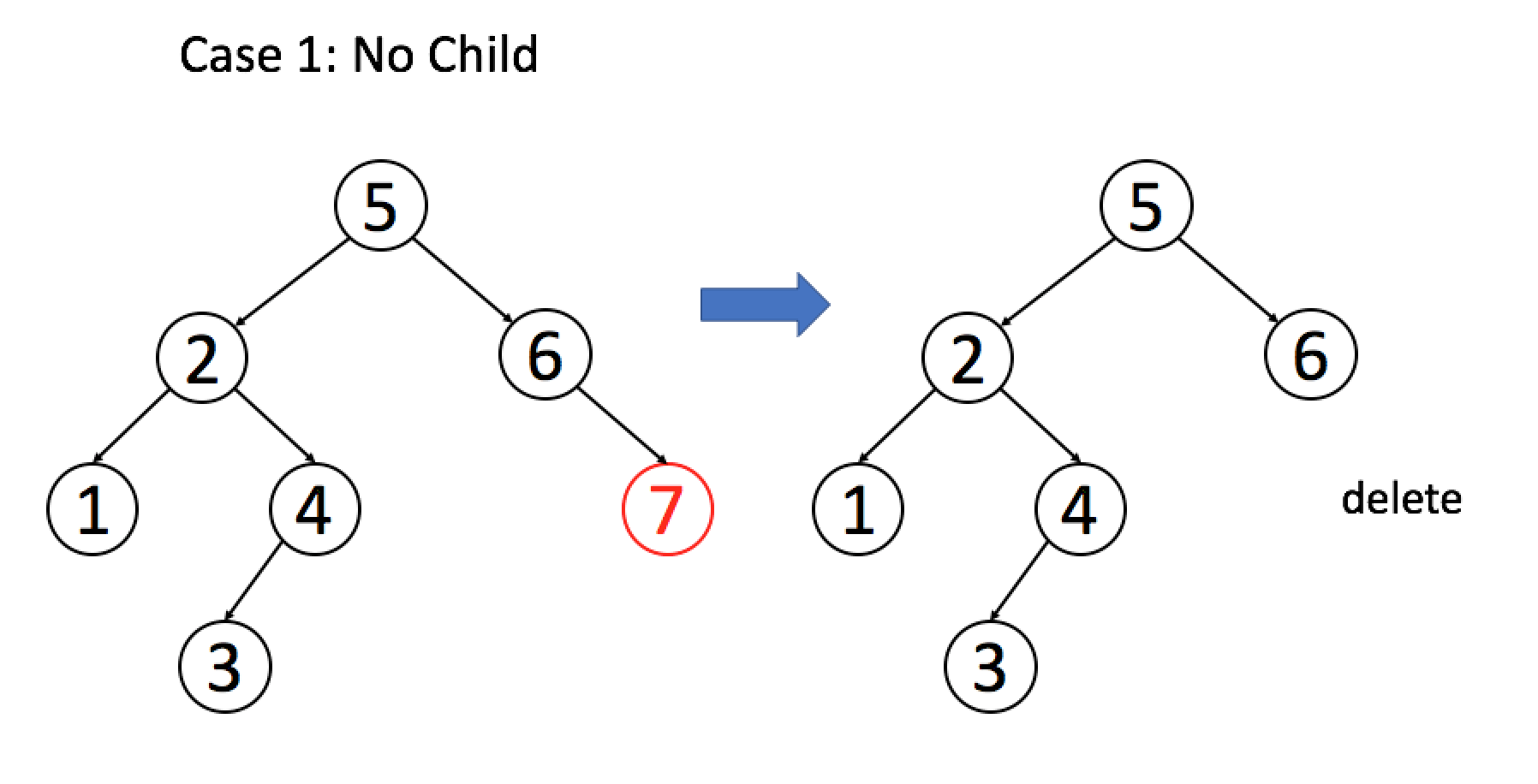
1. 如果目标节点 没有子节点，我们可以直接移除该目标节点。
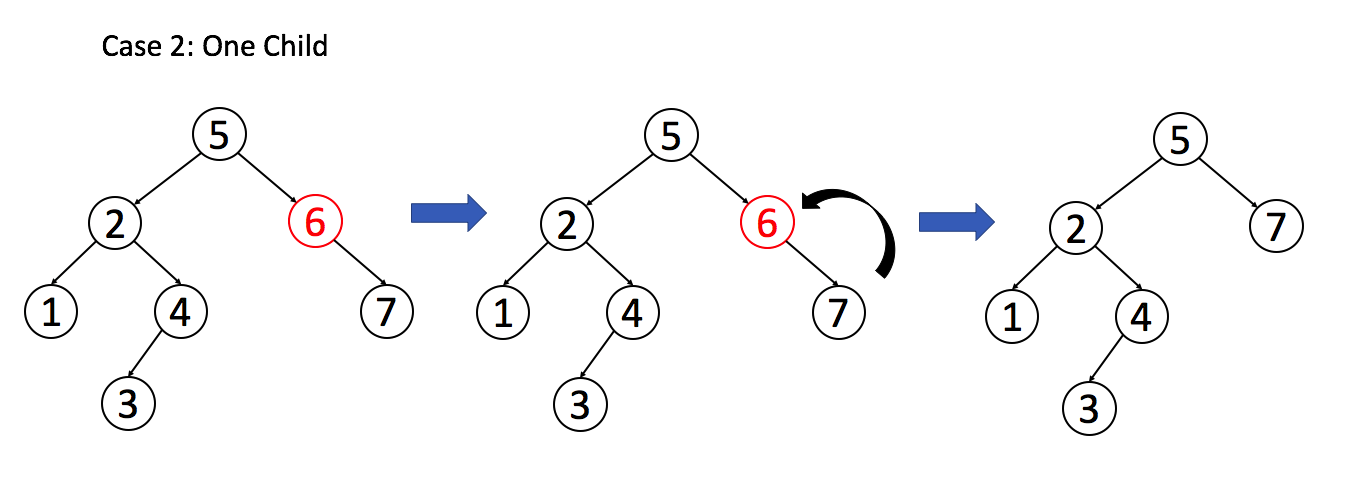
2. 如果目标节点 只有一个子节点，我们可以用其子节点作为替换。
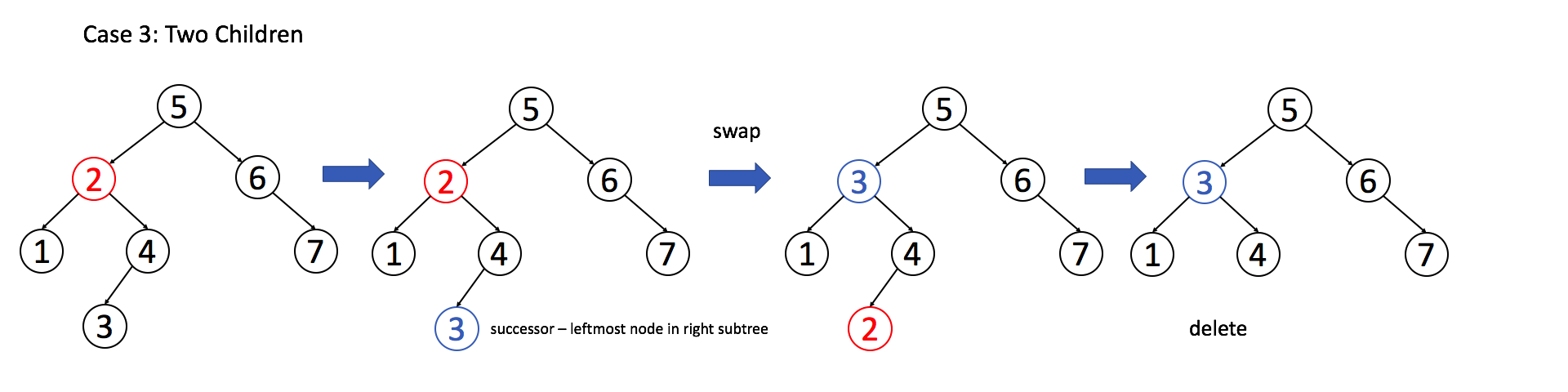
3. 如果目标节点 有两个子节点，我们需要用其中序遍历后继节点或者前驱节点来替换，再删除该目标节点。

例 1：目标节点没有子节点

例 2：目标节只有一个子节点

例 3：目标节点有两个子节点

• 前驱节点（中序遍历中当前节点的前一个节点）：
  1. 访问当前节点的左子节点
  2. 一直访问右子节点，直到没有后续右子节点
• 后继节点（中序遍历中当前节点的后一个节点）：
  1. 访问当前节点的右子节点
  2. 一直访问左子节点，直到没有后续左子节点

     查找最大（小）节点

     查找前驱（后继）节点

     见上图

     输出有序数列（排序）

     重复数据处理

     如果存储的两个对象键值相同，这种情况该怎么处理呢？

常见的处理方式有如下两种

链表/数组/红黑树等

类似hash表的hash冲突解决方式，每一个节点不仅会存储一个数据，因此我们通过链表和支持动态扩容的数组等数据结构，把值相同的数据都存储在同一个节点上。

存储在其右节点

在查找插入位置的过程中，如果碰到一个节点的值，与要插入数据的值相同，我们就将这个要插入的数据放到这个节点的右子树

同时搜索的时候搜索到指定节点也不要停止搜索，而是要继续搜索其右子结点；删除也是一样。

vs 散列表

1. 散列表中的数据是无序存储的，如果要输出有序的数据，需要先进行排序。而对于二叉查找树来说，我们只需要中序遍历，就可以在 O(n) 的时间复杂度内，输出有序的数据序列。
2. 散列表扩容耗时很多，而且当遇到散列冲突时，性能不稳定，尽管二叉查找树的性能不稳定，但是在工程中，我们最常用的平衡二叉查找树的性能非常稳定，时间复杂度稳定在 O(logn)。
3. 笼统地来说，尽管散列表的查找等操作的时间复杂度是常量级的，但因为哈希冲突的存在，这个常量不一定比 logn 小，所以实际的查找速度可能不一定比 O(logn) 快。加上哈希函数的耗时，也不一定就比平衡二叉查找树的效率高。
4. 散列表的构造比二叉查找树要复杂，需要考虑的东西很多。比如散列函数的设计、冲突解决办法、扩容、缩容等。平衡二叉查找树只需要考虑平衡性这一个问题，而且这个问题的解决方案比较成熟、固定。
5. 为了避免过多的散列冲突，散列表装载因子不能太大，特别是基于开放寻址法解决冲突的散列表，不然会浪费一定的存储空间。

   用途

   二叉搜索树的有优点是，即便在最坏的情况下，也允许你在 的时间复杂度内执行所有的搜索、插入、删除操作。

通常来说，如果你想 有序地存储数据或者需要同时执行搜索、插入、删除等多步操作，二叉搜索树这个数据结构是一个很好的选择。

示例

问题描述：设计一个类，求一个数据流中第k大的数。

一个很显而易见的解法是，先将数组降序排列好，然后返回数组中第k个数。

但这个解法的缺点在于，为了在 时间内执行搜索操作，每次插入一个新值都需要重新排列元素的位置。从而使得插入操作的解法平均时间复杂度变为。因此，算法总时间复杂度会变为。

鉴于我们同时需要插入和搜索操作，为什么不考虑使用一个二叉搜索树结构存储数据呢？

对于二叉搜索树的每个节点来说，它的左子树上所有结点的值均小于它的根结点的值，右子树上所有结点的值均大于它的根结点的值。

换言之，对于二叉搜索树的每个节点来说，若其左子树共有m个节点，那么该节点是组成二叉搜索树的有序数组中第m + 1个值。

平衡二叉树

二叉查找树是最常用的一种二叉树，它支持快速插入、删除、查找操作，各个操作的时间复杂度跟树的高度成正比，理想情况下，时间复杂度是 O(logn)。

不过，二叉查找树在频繁的动态更新过程中，可能会出现树的高度远大于 的情况，从而导致各个操作的效率下降。极端情况下，二叉树会退化为链表，时间复杂度会退化到 O(n)。

什么是一个高度平衡的二叉搜索树?

发明平衡二叉查找树这类数据结构的初衷是，解决普通二叉查找树在频繁的插入、删除等动态更新的情况下，出现时间复杂度退化的问题。

所以，平衡二叉查找树中“平衡”的意思，其实就是让整棵树左右看起来比较“对称”、比较“平衡”，不要出现左子树很高、右子树很矮的情况。这样就能让整棵树的高度相对来说低一些，相应的插入、删除、查找等操作的效率高一些。

定义：

一个 高度平衡的二叉搜索树（平衡二叉搜索树） 是在插入和删除任何节点之后，可以自动保持其高度最小。
也就是说，有N个节点的平衡二叉搜索树，它的高度是logN。并且，每个节点的两个子树的高度不会相差超过1。
下面是一个普通二叉搜索树和一个高度平衡的二叉搜索树的例子: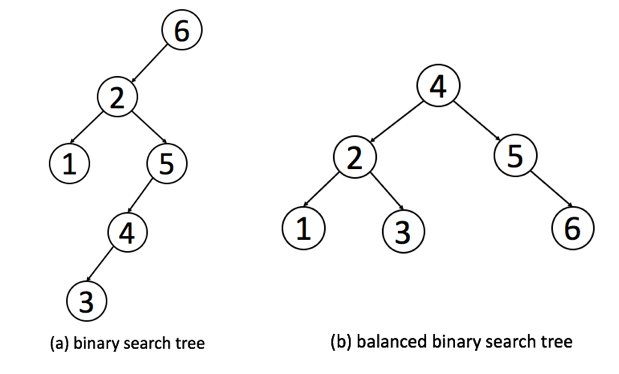

根据定义, 我们可以判断出一个二叉搜索树是否是高度平衡的 (平衡二叉树)。

1. 一个有N个节点的平衡二搜索叉树的高度总是logN。因此，可以计算节点总数和树的高度，以确定这个二叉搜索树是否为高度平衡的。
2. 高度平衡的二叉树每个节点的两个子树的深度不会相差超过1。也可以根据这个性质，递归地验证树。

   为什么需要用到高度平衡的二叉搜索树?

   已经介绍过了二叉树及其相关操作, 包括搜索、插入、删除。 当分析这些操作的时间复杂度时，我们需要注意的是树的高度是十分重要的考量因素。以搜索操作为例，如果二叉搜索树的高度为h，则时间复杂度为。所以二叉搜索树的高度的确很重要。

我们来讨论一下树的节点总数N和高度h之间的关系。 对于一个平衡二叉搜索树, 我们已经在前文中提过。但对于一个普通的二叉搜索树， 在最坏的情况下, 它可以退化成一个链。

因此，具有N个节点的二叉搜索树的高度在logN到N区间变化。也就是说，搜索操作的时间复杂度可以从**logN**变化到**N**。这是一个巨大的性能差异。

所以说，高度平衡的二叉搜索树对提高性能起着重要作用。

如何实现一个高度平衡的二叉搜索树?

有许多不同的方法可以实现。尽管这些实现方法的细节有所不同，但他们有相同的目标:

1. 采用的数据结构应该 满足二分查找属性和高度平衡属性。
2. 采用的数据结构应该 支持二叉搜索树的基本操作，包括在时间内的搜索、插入和删除，即使在最坏的情况下也是如此。

常见的的平衡二叉树：

• 红黑树
• AVL树
• 伸展树
• 树堆

  高度平衡的二叉搜索树的实际应用

高度平衡的二叉搜索树在实际中被广泛使用，因为它可以在时间复杂度内执行所有搜索、插入和删除操作。

平衡二叉搜索树的概念经常运用在Set和Map中。Set和Map的原理相似。 我们将在下文中重点讨论Set这个数据结构。

通常，有两种最广泛使用的集合：散列集合(Hash Set) 和 树集合(Tree Set)。

树集合, Java中的 Treeset 或者C中的 set，是由高度平衡的二叉搜索树实现的。因此，搜索、插入和删除的时间复杂度都是 。

散列集合, Java中的 HashSet 或者C中的 unordered_set，是由哈希实现的, 但是平衡二叉搜索树也起到了至关重要的作用。当存在具有相同哈希键的元素过多时，将花费时间复杂度来查找特定元素，其中N是具有相同哈希键的元素的数量。通常情况下，使用高度平衡的二叉搜索树将把时间复杂度从 改善到 。

哈希集和树集之间的本质区别在于树集中的键是有序的。

参考链接

https://leetcode-cn.com/explore/learn/card/introduction-to-data-structure-binary-search-tree/64/introduction-to-a-bst/170/
https://leetcode-cn.com/explore/learn/card/introduction-to-data-structure-binary-search-tree/65/basic-operations-in-a-bst/173/
https://leetcode-cn.com/explore/learn/card/introduction-to-data-structure-binary-search-tree/65/basic-operations-in-a-bst/175/
https://leetcode-cn.com/explore/learn/card/introduction-to-data-structure-binary-search-tree/65/basic-operations-in-a-bst/179/
https://leetcode-cn.com/explore/learn/card/introduction-to-data-structure-binary-search-tree/66/conclusion/182/
https://leetcode-cn.com/explore/learn/card/introduction-to-data-structure-binary-search-tree/67/appendix-height-balanced-bst/187/
https://time.geekbang.org/column/article/68334