题目

给定正整数 n，找到若干个完全平方数（比如 1, 4, 9, 16, ...）使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。
示例 1:
输入: n = 12
输出: 3
解释: 12 = 4 + 4 + 4.
示例 2:
输入: n = 13
输出: 2
解释: 13 = 4 + 9.

方案一（BFS）

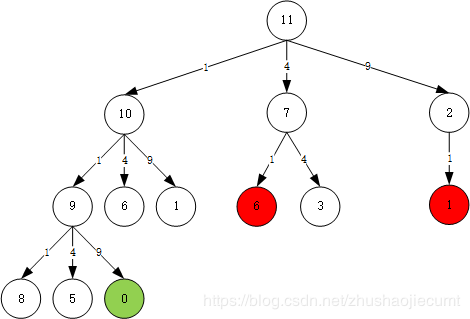
image.png
**

  1. import functools
  2. import collections
  4. class Solution:
  5.     def numSquares(self, n: int) -> int:
  6.         deque = collections.deque([n])
  7.         res = 0
  8.         while deque:
  9.             length = len(deque)
  10.             res += 1
  11.             for _ in range(length):
  12.                 num = deque.popleft()
  13.                 for square_num in self.getSquareNumList(num):
  14.                     t = num - square_num
  15.                     if t == 0:
  16.                         return res
  17.                     deque.append(t)
  18.         return -1
  20.     @functools.lru_cache(maxsize=None)
  21.     def getSquareNumList(self, n: int):
  22.         '''获取小于等于n的完全平方数列表'''
  23.         square_nums = []
  24.         i = 1
  25.         while i * i <= n:
  26.             square_nums.append(i * i)
  27.             i += 1
  29.         return square_nums

方案二（数学定理）

Lagrange 四平方定理： 任何一个正整数都可以表示成不超过四个整数的平方之和。

满足四数平方和定理的数n（这里要满足由四个数构成，小于四个不行），必定满足 完全平方数 - 图2

  1. class Solution:
  2.     def numSquares(self, n: int) -> int:
  3.         if n < 4:
  4.             return n
  5.         # 4^k * (8a + 7)
  6.         while n % 4 == 0:
  7.             n /= 4
  8.         if n % 8 == 7:
  9.             return 4
  11.         a = 0
  12.         while a ** 2 <= n:
  13.             b = int((n - a ** 2) ** 0.5)
  14.             if a ** 2 + b ** 2 == n:
  15.                 return bool(a) + bool(b)
  16.             a += 1
  18.         return 3

方案三（动态规划）

  1. import functools
  3. class Solution:
  4.     def numSquares(self, n: int) -> int:
  5.         # 递推公式
  6.         # dp[i] = min(dp[i], dp[i − j] + 1)
  7.         dp = [i for i in range(n + 1)] # 初始化dp
  8.         for i in range(2, n + 1):
  9.             for j in self.getSquareNumList(i):
  10.                 dp[i] = min(dp[i], dp[i - j] + 1)
  12.         return dp[-1]
  14.     @functools.lru_cache(maxsize=None)
  15.     def getSquareNumList(self, n: int):
  16.         '''获取小于等于n的完全平方数列表'''
  17.         square_nums = []
  18.         i = 1
  19.         while i * i <= n:
  20.             square_nums.append(i * i)
  21.             i += 1
  23.         return square_nums

注意递推公式以及初始化dp

原文

https://leetcode-cn.com/explore/learn/card/queue-stack/217/queue-and-bfs/874/
https://leetcode-cn.com/problems/perfect-squares/solution/dong-tai-gui-hua-bfs-zhu-xing-jie-shi-python3-by-2/