基于Logistic回归的患疝气病马类的存活预测
摘要
患有疝气病的病马存活情况是马类养殖户关心的重要问题。采用二元Logistic回归算法在Horse Colic Data Set数据集上对患病马类的生存情况进行预测,实验采用Accuracy作为评价指标,最优结果为79.41%
1.引言
马常患的疝气病,又称“腹痛”,属于马属动物腹痛性疾病,是世界各国,我国各地,尤其是我国北方各省区的马类最常见的疾病。然而,这种病并不一定源自马的胃肠问题,其他问题也可能引发疝气病,患有疝气病的后马的存活问题是研究一个重点内容。为了更好的预测马类患病后的生存状况,采用逻辑回归算法对马的生存情况进行预测,并进一步探究影响马存活的因素。
2.Logistic回归模型
Logistic回归模型,是指因变量为二分类变量的回归分析。在Horse Colic Data Set数据集中,可将各影响因素作为自变量,而马类存活指标可用1(存活)和0(死亡,安乐死,统称死亡)去表征,是典型的二分类变量。由于因变量的不连续,线性回归将不适用与推导此类自变量和因变量的关系,在此情况下,本研究选用Logistic回归模型解决测类问题,其表达式为:
(1)
(2)
(3)
式中:为事件发生的概率,
为自变量,
为逻辑回归系数,表示自变量发生改变时,马类存活和死亡概率之比的变化值。这一逻辑回归模型可以很好地拟合马类存活结果与马类存活影响因素之间的关系。根据改模型,假定马类存活的概率为P,取值范围为
。以马类存活概率为因变量,各影响因素
为自变量,建立Logistic回归方程,则可得马类存活的概率为:
(4)
这里马类存活的概率表示马类存活的可能性大小,用该公式计算出的定量化数字来表示马类存活的可能性大小,其值越大表示马类存活越有可能发生,反之,则越不可能发生。
3.实验
3.1 数据集
本次实验使用UCL提供的Horse Colic Data Set公开数据集。Horse Colic Data Set数据集于1989-08-06由Mary McLeish & Matt Cecile创建。具体包含368实例具有28个属性(含连续类型属性和离散类型属性),数据集存在约30%的缺失值。数据集缺失程度情况由图1所示: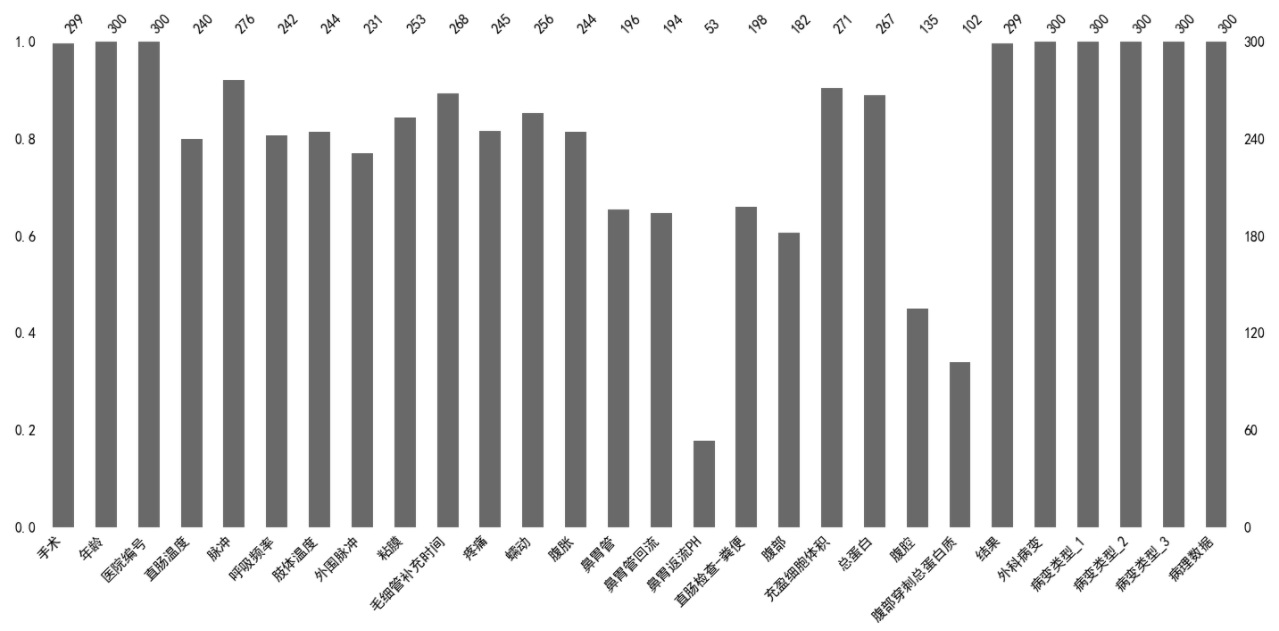
图1 缺失属性展示条形图
数据集缺失分布由图2所示: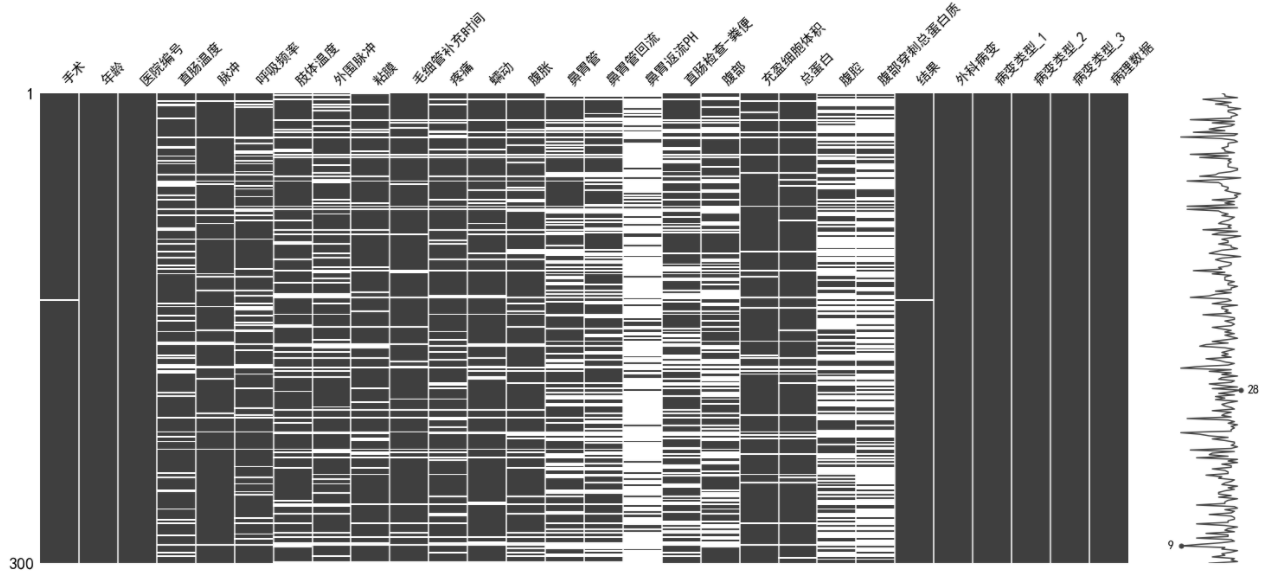
图2 缺失属性展示矩形图
缺失值相关性由图3所示:
图3 缺失属性相关性热力图
3.2 评价标准
在预测任务中,Accuracy是使用比较广泛的评价标准。但是在实际中我们更希望马类能存活下来,所以更偏向于预测到更多的存活的结果。因此,recall召回率可作为另一个评价指标。
3.3 实验分析
数据集中存在大量问题,如数据类型不统一,且存在大量缺失值等。为了能够有效提高模型的表现能力,需要对数据进行预处理,处理步骤如下:
(1)拆分数据属性,并归为连续型变量和离散型变量两类。
(2)对连续型变量进行填充,填充策略采用均值填充;对离散型变量进行填充,填充策略为众数填充。
(3)设置连续型变量的数据类型为float64;离散型变量的数据类型为int64。
(4)删除缺失数量大于120的属性列。
(5)对连续型变量做标准化处理。
对处理完的数据进行可视化分析,找出其中对结果影响较高的因子,相关性矩阵如下图所示: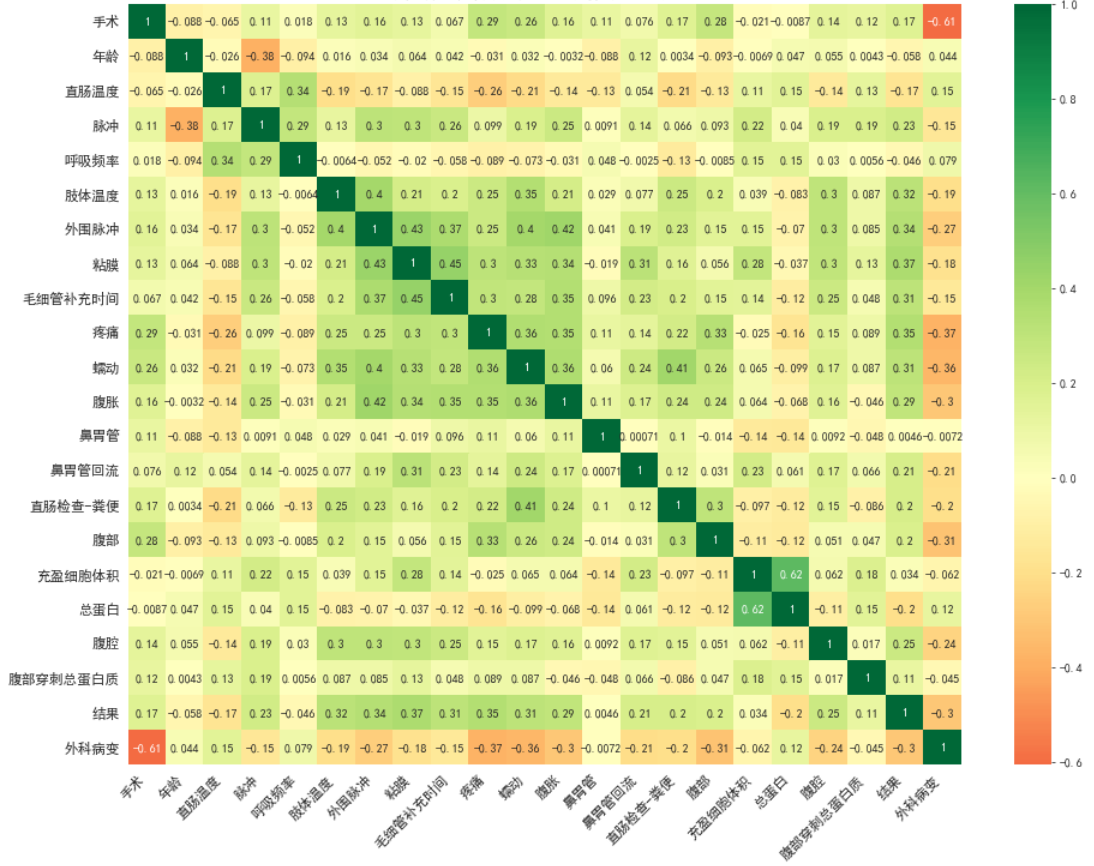
图4 预处理后数据的相关性矩阵图
与结果相关性较大的有:肢体温度 0.32、外围脉搏 0.34、粘膜 0.37、毛细管补充时间 0.31、疼痛程度 0.35、蠕动 0.31、腹胀 0.29和外科病变 -0.3,上述相关的指标对马存活的相关性比较高。在Logistic回归模型的参数设置中,通过比较L1,L2正则化强度因子,查看模型交叉验证的表现,如下图4所示: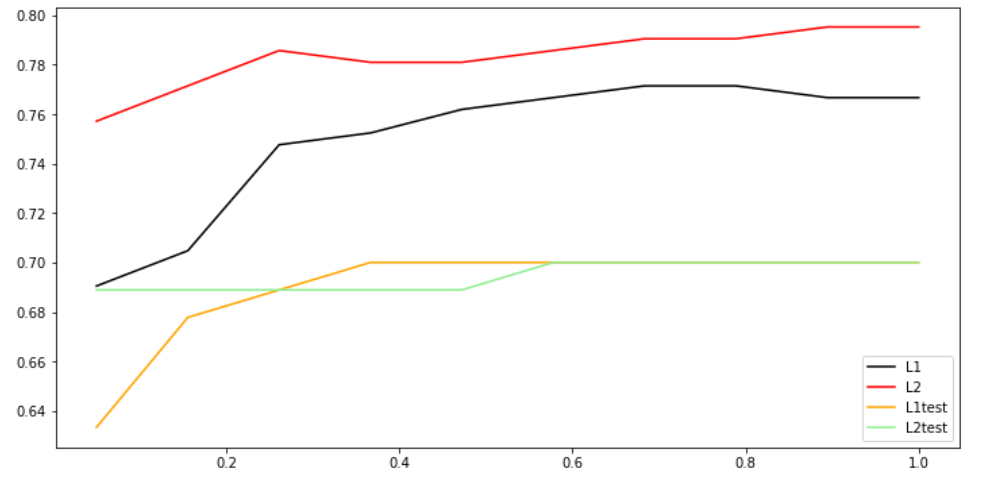
图6 L1和L2正则化交叉验证比较图
可以直观的看到L1正则化过拟合程度更平滑,经过多次调优综合选择,Logistic回归模型在ACC上取得最好效果为79.41%,最优参数如下表所示:
表1 模型参数表
| 参数 | 参数值 |
|---|---|
| penalty | l2 |
| C | 0.5777777777777778 |
| max_iter | 1000 |
| solver | liblinear |
4.结束语
本文仅单用逻辑回归作为预测手段,经过多次调优后从71.02%的正确率提升到最优的79.41%,单模型效果的比较有限。后续,将在更多算法模型上进行预测,横向比较多个模型 ;通过特征工程或集成融合多个模型,纵向对比单模型,以提高预测正确率。
5.附件
数据处理部分源码:
数据可视化部分源码:
数据可视化.ipynb
逻辑回归部分源码:
逻辑回归算法.ipynb

