1. **前言：**秩和检验（Rank sum tes）的定义和应用范围这里不多复述，网上有各种资源，需要注意的是两点：①秩和检验是一种**非参数检验法**, 它是一种用样本秩来代替样本值的检验法；②秩和检验**可以用于样本容量不相等**的两个或多个样本。<br />    **本文介绍如何在R上进行Kruskal–Wallis秩和检验。**<br />   参考文献：<br />   [基于R软件的多组独立样本秩和检验的多重比较_金英良.pdf](https://www.yuque.com/attachments/yuque/0/2019/pdf/119869/1551270418162-8c76a1e3-b89b-4856-9dbb-91c47bb46722.pdf?_lake_card=%7B%22uid%22%3A%22rc-upload-1551270384124-3%22%2C%22src%22%3A%22https%3A%2F%2Fwww.yuque.com%2Fattachments%2Fyuque%2F0%2F2019%2Fpdf%2F119869%2F1551270418162-8c76a1e3-b89b-4856-9dbb-91c47bb46722.pdf%22%2C%22name%22%3A%22%E5%9F%BA%E4%BA%8ER%E8%BD%AF%E4%BB%B6%E7%9A%84%E5%A4%9A%E7%BB%84%E7%8B%AC%E7%AB%8B%E6%A0%B7%E6%9C%AC%E7%A7%A9%E5%92%8C%E6%A3%80%E9%AA%8C%E7%9A%84%E5%A4%9A%E9%87%8D%E6%AF%94%E8%BE%83_%E9%87%91%E8%8B%B1%E8%89%AF.pdf%22%2C%22size%22%3A171203%2C%22type%22%3A%22application%2Fpdf%22%2C%22ext%22%3A%22pdf%22%2C%22progress%22%3A%7B%22percent%22%3A0%7D%2C%22status%22%3A%22done%22%2C%22percent%22%3A0%2C%22card%22%3A%22file%22%7D)

1.示例数据

现在有三组数据A，B，C需要进行Kruskal–Wallis秩和检验，检验这三组数据是否差异显著，三组示例数据如下：
A：3.5，4.0，6.7，5.6，8.9，7.8**（样本容量为6）
B：4.5，3.0，8.0，5.4，6.9，2.8，7.7，3.9**（样本容量为8）
C: 2.1，4.8，3.3，8.8**（样本容量为4）**

2.安装相关包

  1. 分析前，先在R上安装包**“spdep”**和包**“pgirmess”。**

install.packages(“spdep”) install.packages(“pgirmess”)

3.分析方法

先使用该软件的核心包（自带的）进行多组独立样本Kruskal–Wallis秩和检验（即先总的检验多个样本数据的差异是否显著），再采用R语言软件的“pgirmess”统计包的kruskalmc函数进行Kruskal–Wallis秩和检验的两两样本比较。（即再对多个样本进行两两差异的显著性分析）
**

4.Kruskal–Wallis秩和检验

下面介绍两种对原始处理数据的不同的处理方法来进行秩和检验。

（1）方法一（直接法）

这种方法是直接在R语言的命令界面里写入要处理的数据，适合小数据集。

library(spdep) library(pgirmess) A=c(3.5,4.0,6.7,5.6,8.9,7.8) B=c(4.5,3.0,8.0,5.4,6.9,2.8,7.7,3.9) C=c(2.1,4.8,3.3,8.8) jianyan=list(A,B,C)

kruskal.test(jianyan) #①Kruskal-Wallis检验，先打印总体比较的p值

运行结果如下：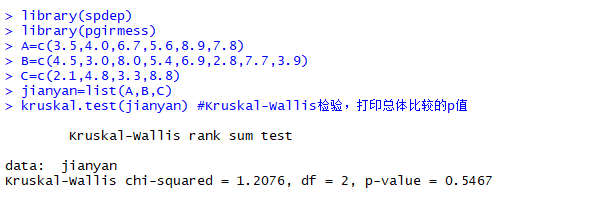
在R语言上做Kruskal–Wallis秩和检验 - 图1
然后进行两两样本的秩和检验：

resp<-c(3.5,4.0,6.7,5.6,8.9,7.8,4.5,3.0,8.0,5.4,6.9,2.8,7.7,3.9,2.1,4.8,3.3,8.8) #将A，B，C三组数据依次放在一个向量里 categ<-factor(rep(1:3,c(6,8,4))) #6,8,4依次为A,B,C对应的样本容量

kruskalmc(resp, categ, probs=0.05) #②再使用kruskalmc函数做两两样本的比较

运行结果如下：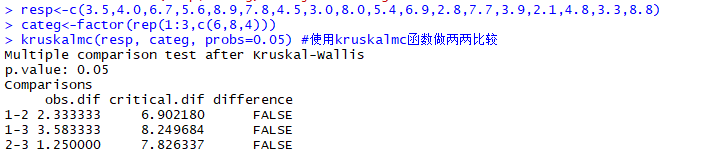
在R语言上做Kruskal–Wallis秩和检验 - 图2
————————————————————————————————————————————————————
【题外话：Kruskal–Wallis秩和检验有时得不到精确的p值，对于Kruskal–Wallis秩和检验差异显著的多个样本，想知道具体差异在哪些样本之间同时又想获得精确的p值，可以采用Nemenyi进行两两样本检验，方法如下】

install.packages(“PMCMRplus”) library(PMCMRplus) library(PMCMR) posthoc.kruskal.nemenyi.test(jianyan) #未校正

运行结果如下：
在R语言上做Kruskal–Wallis秩和检验 - 图3

posthoc.kruskal.nemenyi.test(jianyan,dist=”Chisq”) #校正

运行结果如下：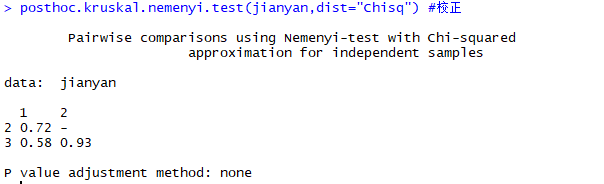
在R语言上做Kruskal–Wallis秩和检验 - 图4
—————————————————————————————————————————————————————-

（2）方法二（表格数据导入法）

先将三组数据放于.csv表格里，表格里的数据的格式如下：
示例数据附件如下：
table.csv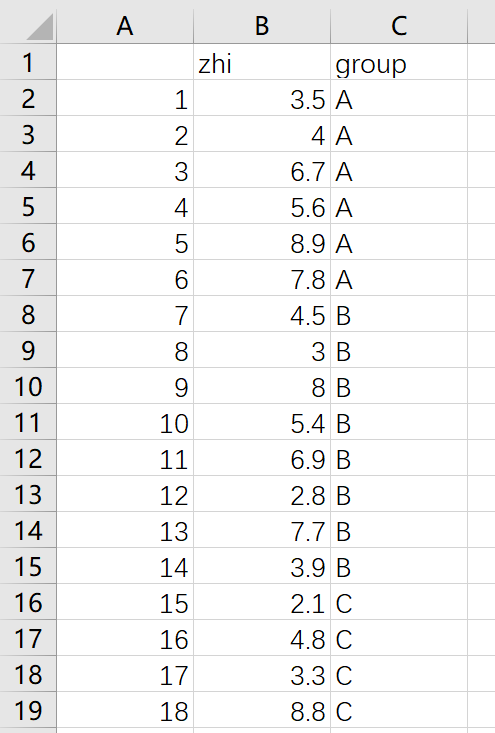
在R语言上做Kruskal–Wallis秩和检验 - 图5

R中输入代码如下：

cd <- read.csv(“table.csv”)#读入数据，建立数据集cd，此处假设table.csv文件已经放在工作目录之下 cd$group <- as.factor(cd$group) kruskal.test(zhi~group, data=cd) #①Kruskal-Wallis检验，先打印总体比较的p值

运行结果如下：
在R语言上做Kruskal–Wallis秩和检验 - 图6

此时假设 “spdep”包和“pgirmess”包已经安装，再进行Kruskal–Wallis秩和检验的两两样本比较如下：

library(pgirmess) library(coin) library(multcomp) kruskalmc(zhi~group, data=cd, probs=0.05) #②再使用kruskalmc函数做两两样本的比较

运行结果如下：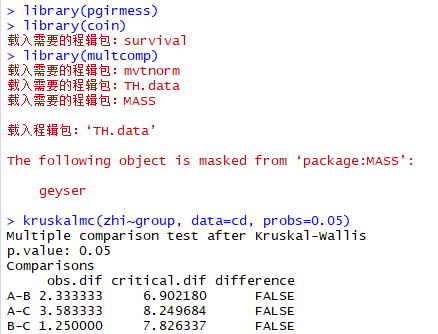
在R语言上做Kruskal–Wallis秩和检验 - 图7
——————————————————————————————————————————————-
PS：使用table.csv里的数据进行Nemenyi检验流程如下：

library(PMCMR) posthoc.kruskal.nemenyi.test(zhi~group,data=cd) #未校正

运行结果如下：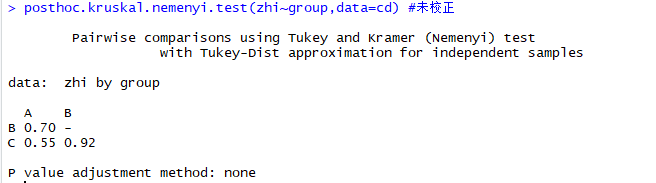
在R语言上做Kruskal–Wallis秩和检验 - 图8

posthoc.kruskal.nemenyi.test(zhi~group,data=cd,dist=”Chisq”) #校正

运行结果如下：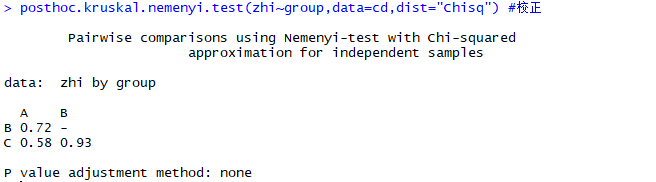
在R语言上做Kruskal–Wallis秩和检验 - 图9
————————————————————————————————————————————————
2019年2月27日初稿

转载请注明出处。如有错误，欢迎及时与我反馈，一起交流学习。