转载来源：https://github.com/emvolz/treedater

Molecular Clock Dating of Influenza H3N2

Erik Volz

2018-05-02

Introduction

treedater fits a strict or relaxed molecular clock to a phylogenetic tree and estimates evolutionary rates and times of common ancestry. The calendar time of each sample must be specified (possibly with bounds of uncertainty) and the length of the sequences used to estimate the tree.
treedater uses heuristic search to optimise the TMRCAs of a phylogeny and the substitution rate. An uncorrelated relaxed molecular clock accounts for rate variation between lineages of the phylogeny which is parameterised using a Gamma-Poisson mixture model.
To cite:

The most basic usage is

  1. dater( tre, sts, s)

where

  • tre is an ape::phylo phylogeny,
  • sts is a named vector of sample times for each tip in tre
  • s is the length of the genetic sequences used to estimate tre

    Invoking treedater from the command line

    You can also use treedater from the command line without starting R using the tdcl script:
    1. ./tdcl -h
    2. Usage: ./tdcl [-[-help|h] [<logical>]] [-[-treefn|t] <character>] [-[-samplefn|s] <character>] [-[-sequenceLength|l] <double>] [-[-output|o] [<character>]]
    3. -t <file> : file name of tree in newick format  
    4. -s  <file> : should be a comma-separated-value file with sample times in format <taxon-id,sample-time> and no header
    5. -l <length> :  the integer length of sequences in alignment used to construct the tree 
    6. -o <file>: name of file for saving output
    Note that you may need to modify the first line of the tdcl script with the correct path to Rscript or littler.

    Influenza H3N2 HA

    This data set comprises 177 HA sequences collected over 35 years worldwide with known date of sampling. We estimated a maximum likelihood tree using iqtree. We will use the sample dates and ML tree to fit a molecular clock and estimate a dated phylogeny. First, load the tree (any method can be used to load a phylogeny into ape::phylo format):
    1. require(treedater)
    2. #> Loading required package: treedater
    3. #> Loading required package: limSolve
    4. (tre <- ape::read.tree( system.file( 'extdata', 'flu_h3n2_final_small.treefile', package='treedater') ))
    5. #> 
    6. #> Phylogenetic tree with 177 tips and 175 internal nodes.
    7. #> 
    8. #> Tip labels:
    9. #>  HM628693_2010-03-03, KC883039_2011-04-04, KC882820_2011-01-04, GQ983548_2009-06-22, KF790184_2012-10-05, JX978746_2012-03-19, ...
    10. #> 
    11. #> Unrooted; includes branch lengths.
    Note that this tree does not have a root, and in the process of fitting a molecular clock, we will estimate the best root location.
    1. seqlen <- 1698 # the length of the HA sequences used to reconstruct the phylogeny
    To fit the molecular clock, we will need the sample time for each lineage. Note that the date of sampling is incorporated into the name of each lineage, which is common in viral phylogenetics studies. The package includes a convenient function for extracting these dates:
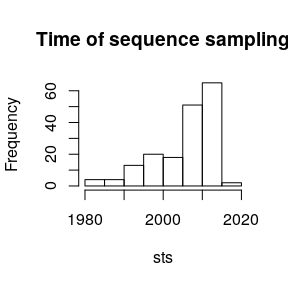
    1. sts <- sampleYearsFromLabels( tre$tip.label, delimiter='_' )
    2. head(sts)
    3. #> HM628693_2010-03-03 KC883039_2011-04-04 KC882820_2011-01-04 
    4. #>            2010.167            2011.255            2011.008 
    5. #> GQ983548_2009-06-22 KF790184_2012-10-05 JX978746_2012-03-19 
    6. #>            2009.471            2012.760            2012.213
    How are samples distributed through time?
    1. hist( sts , main = 'Time of sequence sampling')
    image.png
    The basic usage of the treedater algorithm is as follows:
    1. (dtr <- dater( tre , sts, seqlen ))
    2. #> Note: Minimum temporal branch length  (*minblen*) set to 0.0192816582316329. Increase *minblen* in the event of convergence failures. 
    3. #> Tree is not rooted. Searching for best root position. Increase searchRoot to try harder.
    4. #> 
    5. #> Phylogenetic tree with 177 tips and 176 internal nodes.
    6. #> 
    7. #> Tip labels:
    8. #>  HM628693_2010-03-03, KC883039_2011-04-04, KC882820_2011-01-04, GQ983548_2009-06-22, KF790184_2012-10-05, JX978746_2012-03-19, ...
    9. #> 
    10. #> Rooted; includes branch lengths.
    11. #> 
    12. #>  Time of common ancestor 
    13. #> 1979.4372056481 
    14. #> 
    15. #>  Time to common ancestor (before most recent sample) 
    16. #> 35.6066299683389 
    17. #> 
    18. #>  Mean substitution rate 
    19. #> 0.00321644725184376 
    20. #> 
    21. #>  Strict or relaxed clock 
    22. #> relaxed 
    23. #> 
    24. #>  Coefficient of variation of rates 
    25. #> 0.406223621791838
    This produces a rooted tree with branches in calendar time. Note that if we invoked dater with a rooted input tree, it would not estimate the root position. In this way, you can also set the root location in other ways, such as by using an outgroup.
    Lets see how long it takes to run treedater:
    1. rt0 <- Sys.time()
    2. dtr <- dater( tre , sts, seqlen )
    3. #> Note: Minimum temporal branch length  (*minblen*) set to 0.0192816582316329. Increase *minblen* in the event of convergence failures. 
    4. #> Tree is not rooted. Searching for best root position. Increase searchRoot to try harder.
    5. rt1 <- Sys.time()
    6. rt1 - rt0 
    7. #> Time difference of 2.42605 secs
    Note the returned value includes estimated substition rates and TMRCAs. The dtr object extends ape::phylo, so most of the methods that you can use in other R packages that use that format can also be used with a dater object. Lets plot the tree.
    1. plot( dtr , no.mar=T, cex = .2 )
    image.png
    It looks like there are a couple of recent lineages that dont seem to fit well with the ladder-like topology. We will examine this in the next section.

    Detecting and removing outliers / testing for relaxed clock

    To find lineages that dont fit the molecular clock model very well, run
    1. outliers <- outlierTips( dtr , alpha = 0.20) 
    2. #>                                   taxon          q            p     loglik
    3. #> KF805656_2013-02-21 KF805656_2013-02-21 0.03343122 0.0001888769 -10.256192
    4. #> KF805696_2013-02-27 KF805696_2013-02-27 0.12141536 0.0013719249  -7.648289
    5. #> KJ955531_2010-08-22 KJ955531_2010-08-22 0.13001919 0.0035424231  -7.123249
    6. #> KC883315_2010-11-24 KC883315_2010-11-24 0.13001919 0.0036728583  -6.299932
    7. #> CY113269_1980-12-01 CY113269_1980-12-01 0.13001919 0.0032751896  -6.342361
    8. #> KP765772_2014-01-01 KP765772_2014-01-01 0.19834490 0.0067235559  -8.163295
    9. #>                            rates branch.length
    10. #> KF805656_2013-02-21 0.0005415686    14.6935259
    11. #> KF805696_2013-02-27 0.0087076751     0.8178460
    12. #> KJ955531_2010-08-22 0.0085105748     1.2451030
    13. #> KC883315_2010-11-24 0.0011936366     1.6149868
    14. #> CY113269_1980-12-01 0.0071869330     0.4813258
    15. #> KP765772_2014-01-01 0.0009823168    33.5660253
    This returns a table in ascending order showing the quality of the molecular clock model fit for each lineage. Now lineages could be selected for removal in various ways. Lets remove all tips that dont have a very high q-value :
    1. tre2 <- ape::drop.tip( tre, rownames(outliers[outliers$q < 0.20,]) )
    Now we can rerun dater with the reduced tree:
    1. (dtr2 <- dater(tre2, sts, seqlen, ncpu = 1) ) # increase ncpu to use parallel computing
    2. #> Note: Minimum temporal branch length  (*minblen*) set to 0.0190819514539775. Increase *minblen* in the event of convergence failures. 
    3. #> Tree is not rooted. Searching for best root position. Increase searchRoot to try harder.
    4. #> 
    5. #> Phylogenetic tree with 171 tips and 170 internal nodes.
    6. #> 
    7. #> Tip labels:
    8. #>  HM628693_2010-03-03, KC883039_2011-04-04, KC882820_2011-01-04, GQ983548_2009-06-22, KF790184_2012-10-05, JX978746_2012-03-19, ...
    9. #> 
    10. #> Rooted; includes branch lengths.
    11. #> 
    12. #>  Time of common ancestor 
    13. #> 1981.41140738388 
    14. #> 
    15. #>  Time to common ancestor (before most recent sample) 
    16. #> 33.632428232555 
    17. #> 
    18. #>  Mean substitution rate 
    19. #> 0.004142128271224 
    20. #> 
    21. #>  Strict or relaxed clock 
    22. #> relaxed 
    23. #> 
    24. #>  Coefficient of variation of rates 
    25. #> 0.232572609267198
    After removing the outliers, the coefficient of variation of rates is much lower, suggesting that a strict clock model may be appropriate for the reduced tree. We can test the suitability of the strict clock with this test:
    1. rct <- relaxedClockTest( tre2, sts, seqlen, ncpu = 1 ) # increase ncpu to use parallel computing
    2. #> Note: Minimum temporal branch length  (*minblen*) set to 0.0190819514539775. Increase *minblen* in the event of convergence failures. 
    3. #> Tree is not rooted. Searching for best root position. Increase searchRoot to try harder.
    4. #> Running in quiet mode. To print progress, set quiet=FALSE.
    5. #> NOTE: Running with overrideSearchRoot will speed up execution but may underestimate variance.
    6. #> NOTE: Running with overrideTempConstraint will speed up execution but may underestimate variance. Bootstrap tree replicates may have negative branch lengths.
    7. #> Note: Minimum temporal branch length  (*minblen*) set to 0.0190819514539775. Increase *minblen* in the event of convergence failures. 
    8. #> Tree is not rooted. Searching for best root position. Increase searchRoot to try harder.
    9. #> Best clock model:  relaxed 
    10. #> Null distribution of rate coefficient of variation: 0 0.000422194273826786 
    11. #> Returning best treedater fit
    Note that the ncpu option enabled parallel computing to speed up this test.
    This test indicates a relaxed clock. Nevertheless, lets re-fit the model to the reduced tree using a strict clock for comparison:
    1. (dtr3 <- dater( tre2, sts, seqlen, strict=TRUE ))
    2. #> Note: Minimum temporal branch length  (*minblen*) set to 0.0190819514539775. Increase *minblen* in the event of convergence failures. 
    3. #> Tree is not rooted. Searching for best root position. Increase searchRoot to try harder.
    4. #> 
    5. #> Phylogenetic tree with 171 tips and 170 internal nodes.
    6. #> 
    7. #> Tip labels:
    8. #>  HM628693_2010-03-03, KC883039_2011-04-04, KC882820_2011-01-04, GQ983548_2009-06-22, KF790184_2012-10-05, JX978746_2012-03-19, ...
    9. #> 
    10. #> Rooted; includes branch lengths.
    11. #> 
    12. #>  Time of common ancestor 
    13. #> 1981.50804415544 
    14. #> 
    15. #>  Time to common ancestor (before most recent sample) 
    16. #> 33.5357914609983 
    17. #> 
    18. #>  Mean substitution rate 
    19. #> 0.00454744152084714 
    20. #> 
    21. #>  Strict or relaxed clock 
    22. #> strict 
    23. #> 
    24. #>  Coefficient of variation of rates 
    25. #> 0
    1. plot( dtr3 , no.mar=T, cex = .2 )
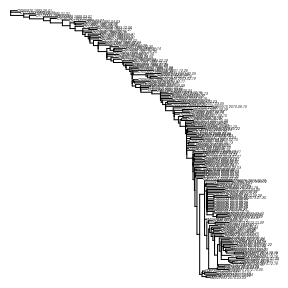
    image.png
    The rate is higher than the initial estimate with the relaxed clock and the recently-sampled outlying lineages have been removed.

    Parametric bootstrap

    Estimating confidence intervals for rates and dates is straightforward using a parametric bootstrap:
    1. rt2 <- Sys.time()
    2. (pb <- parboot( dtr3, ncpu = 1) )# increase ncpu to use parallel computing
    3. #> Running in quiet mode. To print progress, set quiet=FALSE.
    4. #> NOTE: Running with overrideSearchRoot will speed up execution but may underestimate variance.
    5. #> NOTE: Running with overrideTempConstraint will speed up execution but may underestimate variance. Bootstrap tree replicates may have negative branch lengths.
    6. #>                            pseudo ML        2.5 %       97.5 %
    7. #> Time of common ancestor 1.981508e+03 1.980916e+03 1.981966e+03
    8. #> Mean substitution rate  4.547442e-03 4.112521e-03 5.028357e-03
    9. #> 
    10. #>  For more detailed output, $trees provides a list of each fit to each simulation
    11. rt3 <- Sys.time()
    How fast was it? Note that the ncpu option would enable parallel computing.
    1. rt3 - rt2 
    2. #> Time difference of 5.000826 secs
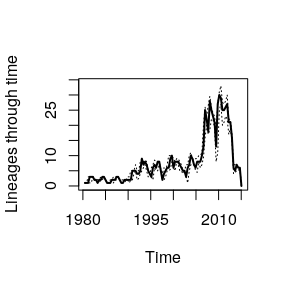
    We can also plot the estimated number of lineages through time with confidence intervals:
    1. plot( pb )
    image.png
    If the ggplot2 package is installed, we can use that instead:
    1. if ( suppressPackageStartupMessages( require(ggplot2)) )
    2. (pb.pl <- plot( pb , ggplot=TRUE) )
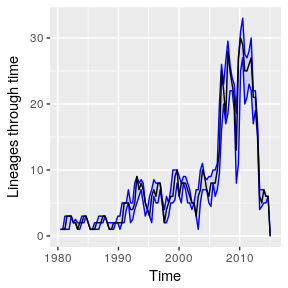
    image.png
    Note repeated bottlenecks and seasonal peaks of LTT corresponding to when samples are taken during seasonal epidemics.
    The package also includes methods for nonparametric bootstrapping if you have already computed a bootstrap distribution of phylogenies.

    Missing sample times

    Suppose we only know some of the sample times to the nearest month, a common occurance in viral phylogenetic studies. To simulate this, we will put uncertainty bounds on some sample times equal to a +/- 2-week window. We create the following data frame with columns lower and upper:
    1. sts.df <- data.frame( lower = sts[1:50] - 15/365, upper = sts[1:50] + 15/365 )
    2. head(sts.df )
    3. #>                        lower    upper
    4. #> HM628693_2010-03-03 2010.126 2010.208
    5. #> KC883039_2011-04-04 2011.214 2011.296
    6. #> KC882820_2011-01-04 2010.967 2011.049
    7. #> GQ983548_2009-06-22 2009.430 2009.512
    8. #> KF790184_2012-10-05 2012.718 2012.801
    9. #> JX978746_2012-03-19 2012.172 2012.254
    In this case, we constructed the data frame with bounds for the first 50 samples in the tree, but we could also manually construct a data frame for a few selected samples where times of sampling are uncertain, or for all of the samples.
    Now re-run treedater with the uncertain sample times. The vector sts provided here gives an initial guess of the unknown sample times.
    1. (dtr4 <- dater( tre2, sts, seqlen, strict = TRUE, estimateSampleTimes = sts.df ) )
    2. #> Note: Minimum temporal branch length  (*minblen*) set to 0.0190819514539775. Increase *minblen* in the event of convergence failures. 
    3. #> Tree is not rooted. Searching for best root position. Increase searchRoot to try harder.
    4. #> 
    5. #> Phylogenetic tree with 171 tips and 170 internal nodes.
    6. #> 
    7. #> Tip labels:
    8. #>  HM628693_2010-03-03, KC883039_2011-04-04, KC882820_2011-01-04, GQ983548_2009-06-22, KF790184_2012-10-05, JX978746_2012-03-19, ...
    9. #> 
    10. #> Rooted; includes branch lengths.
    11. #> 
    12. #>  Time of common ancestor 
    13. #> 1981.54481493773 
    14. #> 
    15. #>  Time to common ancestor (before most recent sample) 
    16. #> 33.515371994552 
    17. #> 
    18. #>  Mean substitution rate 
    19. #> 0.00462062247863572 
    20. #> 
    21. #>  Strict or relaxed clock 
    22. #> strict 
    23. #> 
    24. #>  Coefficient of variation of rates 
    25. #> 0
    Note that the estimated rates and dates didnt change very much due to uncertain sample dates in this case.
    (function () { var script = document.createElement(“script”); script.type = “text/javascript”; script.src = “https://mathjax.rstudio.com/latest/MathJax.js?config=TeX-AMS-MML_HTMLorMML“; document.getElementsByTagName(“head”)[0].appendChild(script); })();