冒泡排序
比较两个相邻的元素,将值大的元素交换到右边
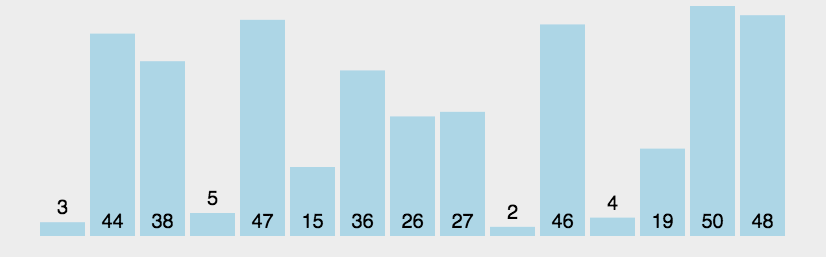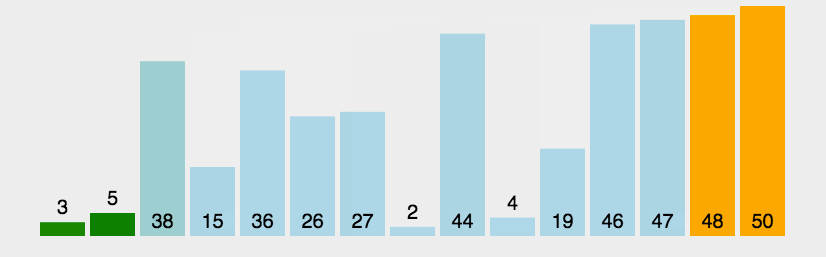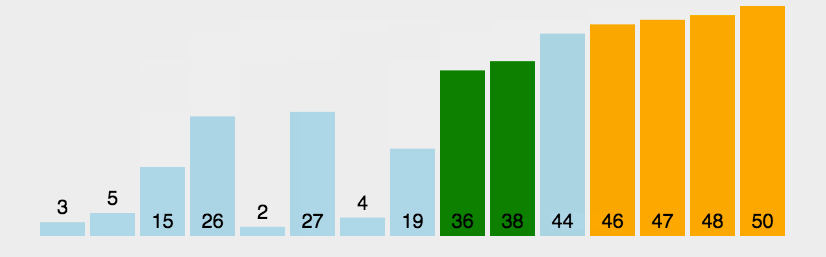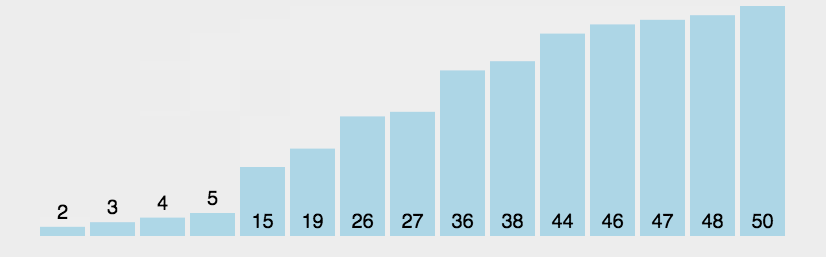
function bubbleSort(arr) {var len = arr.lengthfor(var i = 0; i < len, i++) {for(var j = 0; i < len - i - 1; j++) {if (arr[j] > arr[j+1]) { //相邻元素两两对比var temp = arr[j+1]; //元素交换arr[j+1] = arr[j];arr[j] = temp;}}}}
选择排序
第一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,然后再从剩余的未排序元素中寻找到最小(大)元素,然后放到已排序的序列的末尾。以此类推,直到全部待排序的数据元素的个数为零。
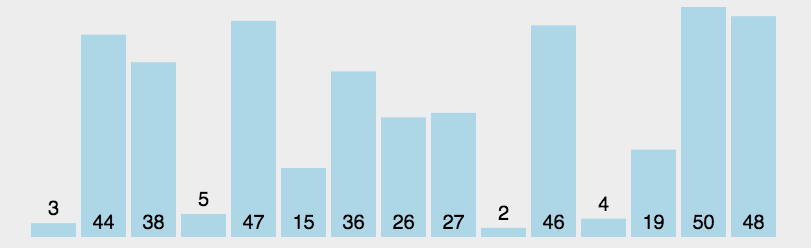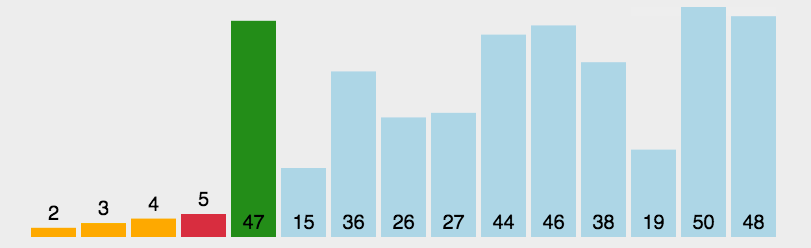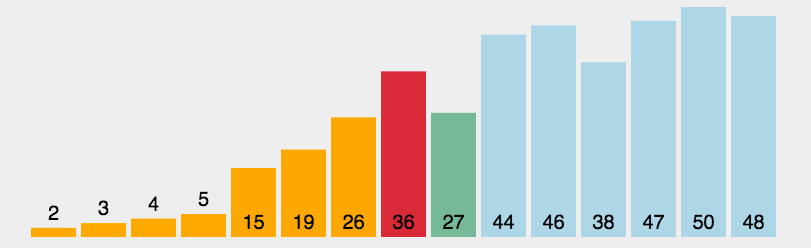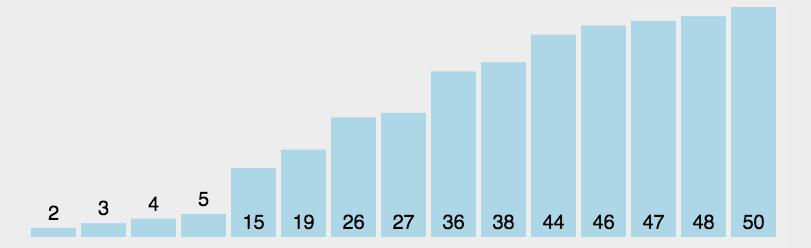
function selectionSort(arr) {var len = arr.length;var minIndex, temp;for (var i = 0; i < len - 1; i++) {minIndex = i;for (var j = i + 1; j < len; j++) {if (arr[j] < arr[minIndex]) { //寻找最小的数minIndex = j; //将最小数的索引保存}}temp = arr[i];arr[i] = arr[minIndex];arr[minIndex] = temp;}return arr;}
插入排序
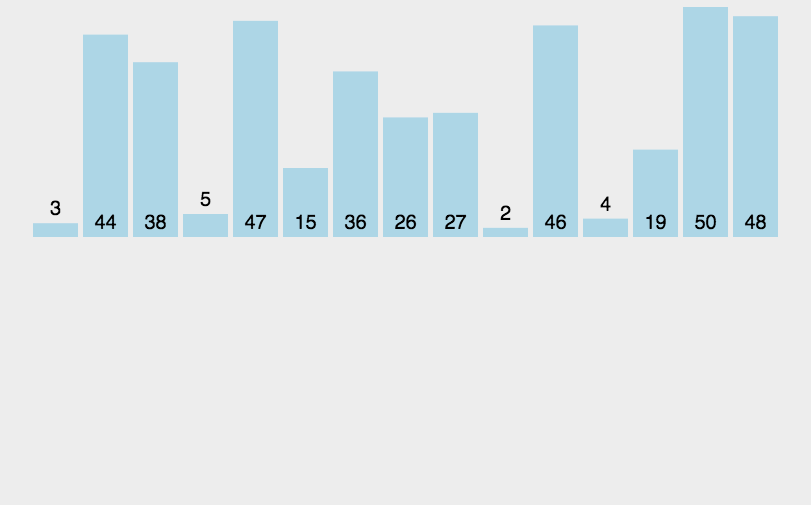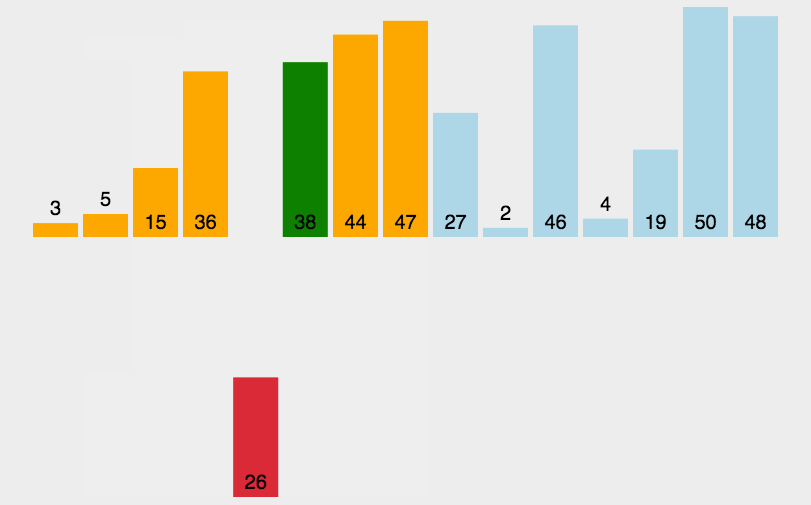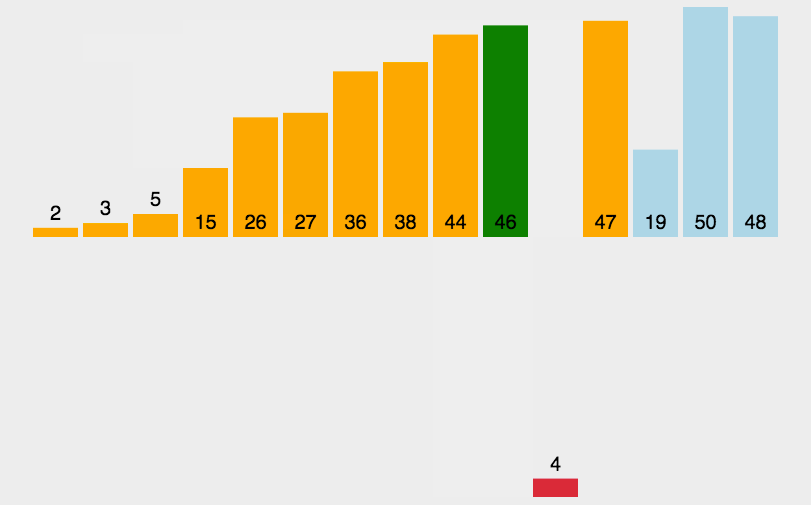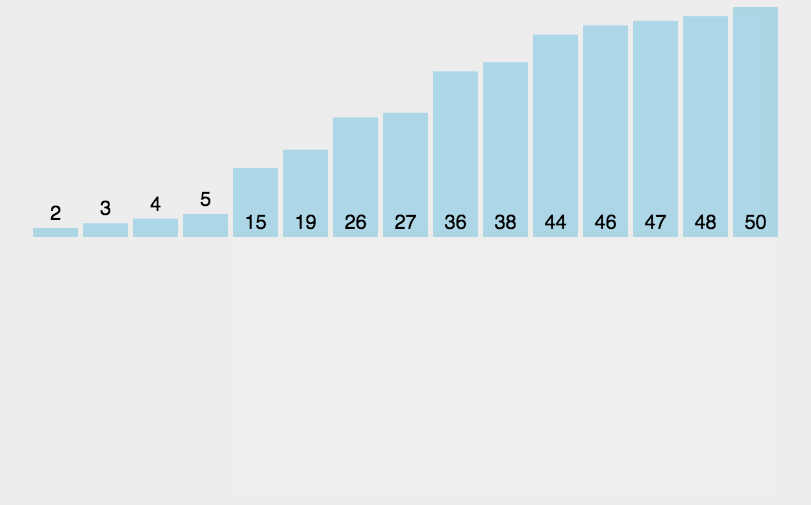
- 从第一个元素开始,该元素默认已经被排序
- 取出下一个元素,在已经排序的元素序列中从后向前扫描
- 如果该元素(已排序)大于新元素,将该元素移到下一位置
- 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置
- 将新元素插入到该位置
- 重复步骤2~5,直到排序完成
function insertionSort(data) {var len = data.length;for (var i = 1; i < len; i++) {var key = data[i];var j = i - 1;while (j >= 0 && data[j] > key) {data[j + 1] = data[j];j--;}data[j + 1] = key;}return data;}
希尔排序
先将整个待排元素序列分割成若干个子序列(由相隔某个“增量”的元素组成的)分别进行直接插入排序,然后依次缩减增量再进行排序,待整个序列中的元素基本有序(增量足够小)时,再对全体元素进行一次直接插入排序。因为直接插入排序在元素基本有序的情况下(接近最好情况),效率是很高的,因此希尔排序在时间效率上有较大提高。
//希尔排序function shallSort(array) {var increment = array.length;var ivar temp; //暂存do {//设置增量increment = Math.floor(increment / 3) + 1;for (i = increment ; i < array.length; i++) {if ( array[i] < array[i - increment]) {temp = array[i];for (var j = i - increment; j >= 0 && temp < array[j]; j -= increment) {array[j + increment] = array[j];}array[j + increment] = temp;}}}while (increment > 1)return array;}
归并排序
把长度为n的输入序列分成两个长度为n/2的子序列;
对这两个子序列分别采用归并排序;
将两个排序好的子序列合并成一个最终的排序序列。
function mergeSort(array) {
var len = array.length;
if (len < 2) {
return array;
}
var middle = Math.floor(len / 2),
left = array.slice(0, middle),
right = array.slice(middle);
return merge(mergeSort(left), mergeSort(right));
}
function merge(left, right) {
var result = [];
while (left.length && right.length) {
if (left[0] <= right[0]) {
result.push(left.shift());
} else {
result.push(right.shift());
}
}
while (left.length)
result.push(left.shift());
while (right.length)
result.push(right.shift());
return result;
}
快速排序
该算法首先要从数列中选出一个元素作为基数(pivot)。接着所有的数据都将围绕这个基数进行,将小于改基数的元素放在它的左边,大于或等于它的数全部放在它的右边,对左右两个小数列重复上述步骤,直至各区间只有1个数。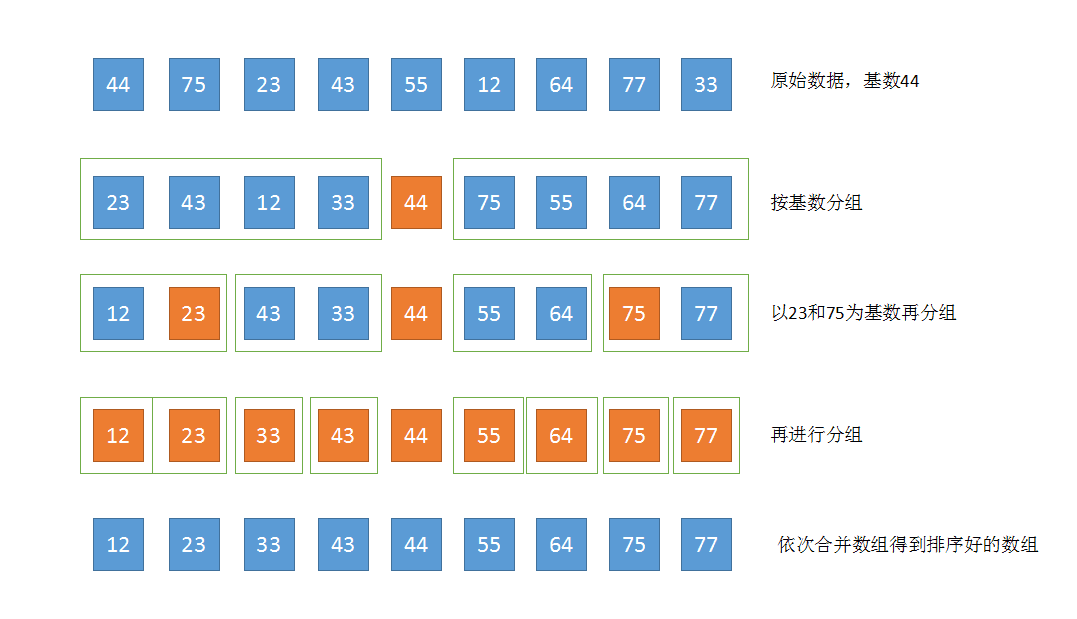
function quickSort(arr) {
if (arr.length == 0) {
return [];
}
var left = [];
var right = [];
var pivot = arr[0];
for (var i = 1; i < arr.length; i++) {
if (arr[i] < pivot) {
left.push(arr[i]);
} else {
right.push(arr[i]);
}
}
return quickSort(left).concat(pivot, quickSort(right));
}
堆排序
大顶堆:每个节点的值都大于或等于其子节点的值,在堆排序算法中用于升序排列
小顶堆:每个节点的值都小于或等于其子节点的值,在堆排序算法中用于降序排列
// 实现大顶堆
const d = 2;
function heap() {
this.heap = []
}
function parent(i) {
return Math.floor((i - 1) / d);
}
function kthChild(i, k) {
return d * i + k;
}
function heapifyUp(heap, i) {
var insertValue = heap[i];
while (i > 0 && insertValue > heap[parent(i)]) {
heap[i] = heap[parent(i)];
i = parent(i);
}
heap[i] = insertValue;
}
function heapifyDown(heap, i) {
var child,temp = heap[i];
while (kthChild(i, 1) < heap.length) {
child = maxChild(i);
if (temp >= heap[child]) {
break;
}
heap[i] = heap[child];
i = child;
}
heap[i] = temp;
}
function maxChild(i) {
var leftChild = kthChild(i, 1);
var rightChild = kthChild(i, 2);
return heap[leftChild] > heap[rightChild] ? leftChild : rightChild;
}
heap.prototype.insert = function(x) {
this.heap.push(x)
heapifyUp(this.heap, this.heap.length - 1)
}
heap.prototype.delete = function(x) {
var maxElement = this.heap[x];
this.heap[x] = this.heap[this.heap.length - 1];
heapifyDown(this.heap, x);
return maxElement;
}
// 排序
function heapSort(arr) {
var Heap = new heap()
for (var i = arr.length-1; i > 0; i--) {
Heap.insert(arr[i], 0);
}
}
计数排序
计数排序的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。
作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。

function countingSort(arr, maxValue) {
var bucket = new Array(maxValue + 1),
sortedIndex = 0;
arrLen = arr.length,
bucketLen = maxValue + 1;
for (var i = 0; i < arrLen; i++) {
if (!bucket[arr[i]]) {
bucket[arr[i]] = 0;
}
bucket[arr[i]]++;
}
for (var j = 0; j < bucketLen; j++) {
while (bucket[j] > 0) {
arr[sortedIndex++] = j;
bucket[j]--;
}
}
return arr;
}
桶排序
桶排序是计数排序的升级版。它利用了函数的映射关系,高效与否的关键就在于这个映射函数的确定。
为了使桶排序更加高效,我们需要做到这两点:
在额外空间充足的情况下,尽量增大桶的数量
使用的映射函数能够将输入的N个数据均匀的分配到K个桶中
function bucketSort(arr, bucketSize) {
if (arr.length === 0) {
return arr;
}
var i;
var minValue = arr[0];
var maxValue = arr[0];
for (i = 1; i < arr.length; i++) {
if (arr[i] < minValue) {
minValue = arr[i]; //输入数据的最小值
} else if (arr[i] > maxValue) {
maxValue = arr[i]; //输入数据的最大值
}
}
//桶的初始化
var DEFAULT_BUCKET_SIZE = 5; //设置桶的默认数量为5
bucketSize = bucketSize || DEFAULT_BUCKET_SIZE;
var bucketCount = Math.floor((maxValue - minValue) / bucketSize) + 1;
var buckets = new Array(bucketCount);
for (i = 0; i < buckets.length; i++) {
buckets[i] = [];
}
//利用映射函数将数据分配到各个桶中
for (i = 0; i < arr.length; i++) {
buckets[Math.floor((arr[i] - minValue) / bucketSize)].push(arr[i]);
}
arr.length = 0;
for (i = 0; i < buckets.length; i++) {
insertionSort(buckets[i]); //对每个桶进行排序,这里使用了插入排序
for (var j = 0; j < buckets[i].length; j++) {
arr.push(buckets[i][j]);
}
}
return arr;
}
基数排序
基数排序有两种方法:
MSD 从高位开始进行排序
LSD 从低位开始进行排序
基数排序 vs 计数排序 vs 桶排序
这三种排序算法都利用了桶的概念,但对桶的使用方法上有明显差异:
基数排序:根据键值的每位数字来分配桶
计数排序:每个桶只存储单一键值
桶排序:每个桶存储一定范围的数值
//LSD Radix Sort
var counter = [];
function radixSort(arr, maxDigit) {
var mod = 10;
var dev = 1;
for (var i = 0; i < maxDigit; i++, dev *= 10, mod *= 10) {
for (var j = 0; j < arr.length; j++) {
var bucket = parseInt((arr[j] % mod) / dev);
if (counter[bucket] == null) {
counter[bucket] = [];
}
counter[bucket].push(arr[j]);
}
var pos = 0;
for (var j = 0; j < counter.length; j++) {
var value = null;
if (counter[j] != null) {
while ((value = counter[j].shift()) != null) {
arr[pos++] = value;
}
}
}
}
return arr;
}