参考资料：

机器学习中的缺失值处理3（机器学习理论若干问题）

数据缺失是数据科学家在处理数据时经常遇到的问题，本文作者基于不同的情境提供了相应的数据插补解决办法。没有完美的数据插补法，但总有一款更适合当下情况。

我在数据清理与探索性分析中遇到的最常见问题之一就是处理缺失数据。首先我们需要明白的是，没有任何方法能够完美解决这个问题。不同问题有不同的数据插补方法——时间序列分析，机器学习，回归模型等等，很难提供通用解决方案。在这篇文章中，我将试着总结最常用的方法，并寻找一个结构化的解决方法。

1 插补数据vs删除数据

在讨论数据插补方法之前，我们必须了解数据丢失的原因。

  • 1、随机丢失（MAR，Missing at Random）：随机丢失意味着数据丢失的概率与丢失的数据本身无关，而仅与部分已观测到的数据有关。

  • 2、完全随机丢失（MCAR，Missing Completely at Random）：数据丢失的概率与其假设值以及其他变量值都完全无关。

  • 3、非随机丢失（MNAR，Missing not at Random）：有两种可能的情况。缺失值取决于其假设值（例如，高收入人群通常不希望在调查中透露他们的收入）；或者，缺失值取决于其他变量值（假设女性通常不想透露她们的年龄，则这里年龄变量缺失值受性别变量的影响）。

在前两种情况下可以根据其出现情况删除缺失值的数据，而在第三种情况下，删除包含缺失值的数据可能会导致模型出现偏差。因此我们需要对删除数据非常谨慎。请注意，插补数据并不一定能提供更好的结果。

2 删除

2.1 列表删除

按列表删除（完整案例分析）会删除一行观测值，只要其包含至少一个缺失数据。你可能只需要直接删除这些观测值，分析就会很好做，尤其是当缺失数据只占总数据很小一部分的时候。然而在大多数情况下，这种删除方法并不好用。因为完全随机缺失（MCAR）的假设通常很难被满足。因此本删除方法会造成有偏差的参数与估计。

  1. newdata <- na.omit(mydata)
  2. # In python
  3. mydata.dropna(inplace=True)

2.2 成对删除

在重要变量存在的情况下，成对删除只会删除相对不重要的变量行。这样可以尽可能保证充足的数据。该方法的优势在于它能够帮助增强分析效果，但是它也有许多不足。它假设缺失数据服从完全随机丢失（MCAR）。如果你使用此方法，最终模型的不同部分就会得到不同数量的观测值，从而使得模型解释非常困难。
缺失值处理3 - 图1
观测行3与4将被用于计算ageNa与DV1的协方差；观测行2、3与4将被用于计算DV1与DV2的协方差。

  1. #Pairwise Deletion
  2. ncovMatrix <- cov(mydata, use="pairwise.complete.obs")
  4. #Listwise Deletion
  5. ncovMatrix <- cov(mydata, use="complete.obs")

2.3 删除变量

在我看来，保留数据总是比抛弃数据更好。有时，如果超过60％的观测数据缺失，直接删除该变量也可以，但前提是该变量无关紧要。话虽如此，插补数据总是比直接丢弃变量好一些。

  1. df <- subset(mydata, select = -c(x,z) )
  2. df <- mydata[ -c(1,3:4) ]
  4. # In python
  5. del mydata.column_name
  6. mydata.drop('column_name', axis=1, inplace=True)

3 时间序列分析专属方法(Time-Series Specific Methods)

前推法（LOCF，Last Observation Carried Forward，将每个缺失值替换为缺失之前的最后一次观测值）与
后推法（NOCB，Next Observation Carried Backward，与LOCF方向相反——使用缺失值后面的观测值进行填补）

这是分析可能缺少后续观测值的纵向重复测量数据的常用方法。纵向数据在不同时间点跟踪同一样本。当数据具有明显的趋势时，这两种方法都可能在分析中引入偏差，表现不佳。

线性插值。此方法适用于具有某些趋势但并非季节性数据的时间序列。

季节性调整+线性插值。此方法适用于具有趋势与季节性的数据。

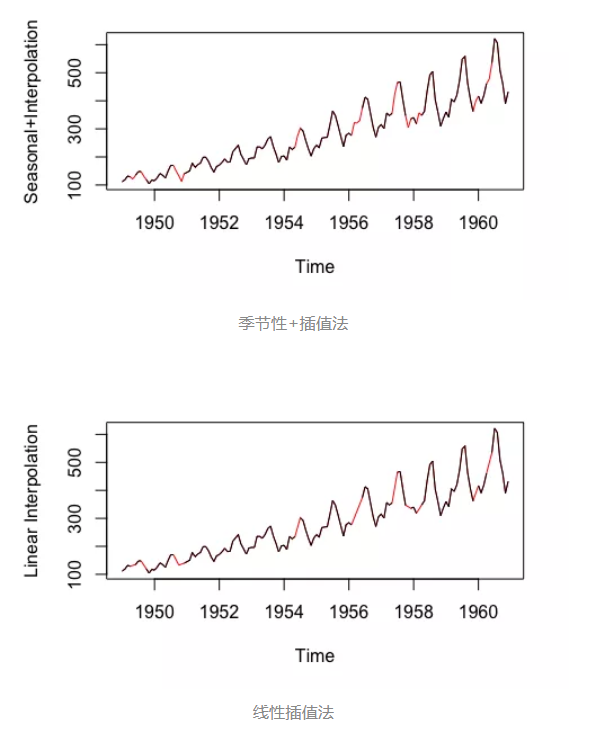
缺失值处理3 - 图2

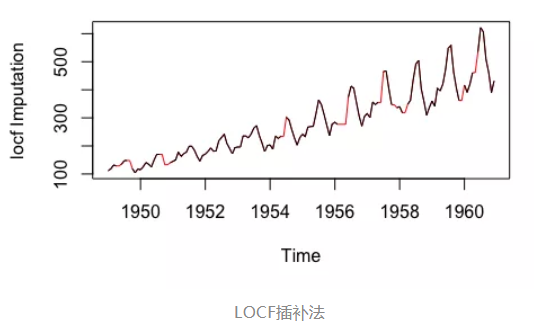
缺失值处理3 - 图3
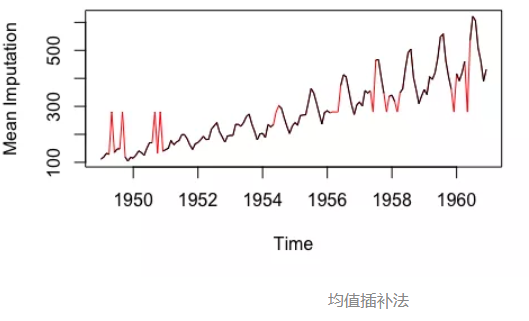
缺失值处理3 - 图4

注：以上数据来自imputeTS库的tsAirgap；插补数据被标红。

  1. library(imputeTS)
  3. na.random(mydata)                  # Random Imputation
  4. na.locf(mydata, option = "locf")   # Last Obs. Carried Forward
  5. na.locf(mydata, option = "nocb")   # Next Obs. Carried Backward
  6. na.interpolation(mydata)           # Linear Interpolation
  7. na.seadec(mydata, algorithm = "interpolation") # Seasonal Adjustment then Linear Interpolation

4 均值，中位数与众数

计算整体均值、中位数或众数是一种非常基本的插补方法，它是唯一没有利用时间序列特征或变量关系的测试函数。该方法计算起来非常快速，但它也有明显的缺点。其中一个缺点就是，均值插补会减少数据的变化差异（方差）。

  1. library(imputeTS)
  3. na.mean(mydata, option = "mean")   # Mean Imputation
  4. na.mean(mydata, option = "median") # Median Imputation
  5. na.mean(mydata, option = "mode")   # Mode Imputation
  7. # In Python
  8. from sklearn.preprocessing import Imputer
  9. values = mydata.values
  10. imputer = Imputer(missing_values=’NaN’, strategy=’mean’)
  11. transformed_values = imputer.fit_transform(values)
  13. # strategy can be changed to "median" and “most_frequent”

5 线性回归

首先，使用相关系数矩阵能够选出一些缺失数据变量的预测变量。从中选择最靠谱的预测变量，并将其用于回归方程中的自变量。缺失数据的变量则被用于因变量。自变量数据完整的那些观测行被用于生成回归方程；其后，该方程则被用于预测缺失的数据点。在迭代过程中，我们插入缺失数据变量的值，再使用所有数据行来预测因变量。重复这些步骤，直到上一步与这一步的预测值几乎没有什么差别，也即收敛。

该方法“理论上”提供了缺失数据的良好估计。然而，它有几个缺点可能比优点还值得关注。首先，因为替换值是根据其他变量预测的，他们倾向于“过好”地组合在一起，因此标准差会被缩小。我们还必须假设回归用到的变量之间存在线性关系——而实际上他们之间可能并不存在这样的关系。

6 多重插补

1、插补：将不完整数据集缺失的观测行估算填充m次（图中m=3）。请注意，填充值是从某种分布中提取的。模拟随机抽取并不包含模型参数的不确定性。更好的方法是采用马尔科夫链蒙特卡洛模拟（MCMC，Markov Chain Monte Carlo Simulation）。这一步骤将生成m个完整的数据集。

2、分析：分别对（m个）每一个完整数据集进行分析。

3、合并：将m个分析结果整合为最终结果。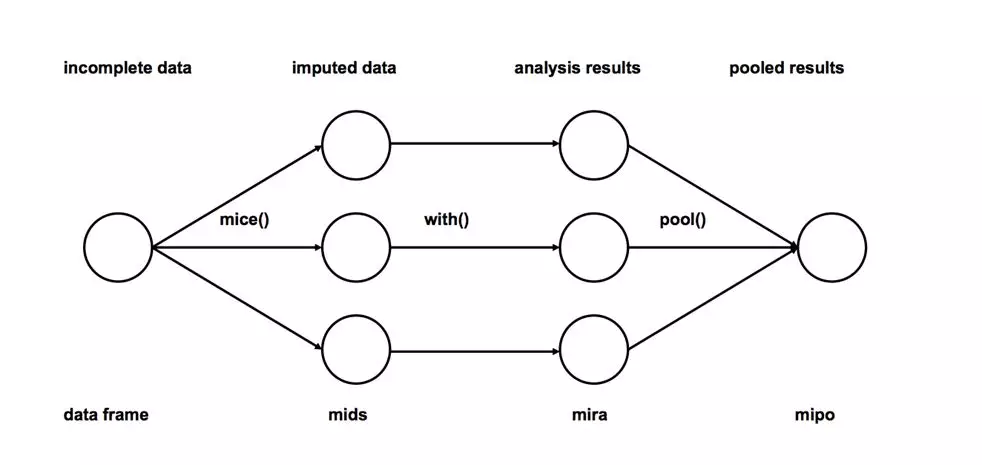
缺失值处理3 - 图5
来源：

http://www.stefvanbuuren.nl/publications/mice in r - draft.pdf

  1. # We will be using mice library in r
  2. library(mice)
  3. # Deterministic regression imputation via mice
  4. imp <- mice(mydata, method = "norm.predict", m = 1)
  6. # Store data
  7. data_imp <- complete(imp)
  9. # Multiple Imputation
  10. imp <- mice(mydata, m = 5)
  12. #build predictive model
  13. fit <- with(data = imp, lm(y ~ x + z))
  15. #combine results of all 5 models
  16. combine <- pool(fit)

这是迄今为止最优选的插补方法，因为它非常易于使用，并且在插补模型正确的情况下它不会引入偏差。

7 分类变量插补

1、众数插补法算是一个法子，但它肯定会引入偏差。

2、缺失值可以被视为一个单独的分类类别。我们可以为它们创建一个新类别并使用它们。这是最简单的方法了。

3、预测模型：这里我们创建一个预测模型来估算用来替代缺失数据位置的值。这种情况下，我们将数据集分为两组：
一组剔除缺少数据的变量（训练组），而另一组则包括缺失变量（测试组）。我们可以用逻辑回归和ANOVA等方法来进行预测。

4、多重插补法。

8 KNN（K近邻）

能够用于数据插补的机器学习方法有很多，比如XGBoost与Random Forest，但在这里我们讨论KNN方法，因为它被广泛应用。在本方法中，我们根据某种距离度量选择出k个“邻居”，他们的均值就被用于插补缺失数据。这个方法要求我们选择k的值（最近邻居的数量），以及距离度量。KNN既可以预测离散属性（k近邻中最常见的值）也可以预测连续属性（k近邻的均值）。

根据数据类型的不同，距离度量也不尽相同：

1、连续数据：最常用的距离度量有欧氏距离，曼哈顿距离以及余弦距离。

2、分类数据：汉明（Hamming）距离在这种情况比较常用。对于所有分类属性的取值，如果两个数据点的值不同，则距离加一。汉明距离实际上与属性间不同取值的数量一致。

KNN算法最吸引人的特点之一在于，它易于理解也易于实现。其非参数的特性在某些数据非常“不寻常”的情况下非常有优势。

KNN算法的一个明显缺点是，在分析大型数据集时会变得非常耗时，因为它会在整个数据集中搜索相似数据点。此外，在高维数据集中，最近与最远邻居之间的差别非常小，因此KNN的准确性会降低。

  1. library(DMwR)
  2. knnOutput <- knnImputation(mydata)
  4. # In python
  5. from fancyimpute import KNN    
  6. # Use 5 nearest rows which have a feature to fill in each row's missing features
  7. knnOutput = KNN(k=5).complete(mydata)

在上述方法中，多重插补与KNN最为广泛使用，而由于前者更为简单，因此其通常更受青睐。

在数据分析和建模中，经常会遇到变量值缺失的情况，这是非常常见的。为了保证数据指标的完整性以及可利用性，通常我们会采取特殊的方式对其进行处理。

1、缺失查看

首先，需要查看缺失值的缺失数量以及比例（#数据使用的kaggle平台上预测房价的数据）

  1. import pandas as pd
  2. # 统计缺失值数量
  3. missing=data.isnull().sum().reset_index().rename(columns={0:'missNum'})
  4. # 计算缺失比例
  5. missing['missRate']=missing['missNum']/data.shape[0]
  6. # 按照缺失率排序显示miss_analy=missing[missing.missRate>0].sort_values(by='missRate',ascending=False)
  7. # miss_analy 存储的是每个变量缺失情况的数据框

柱形图可视化

  1. import matplotlib.pyplot as plt
  2. import pylab as pl
  4. fig = plt.figure(figsize=(18,6))
  5. plt.bar(np.arange(miss_analy.shape[0]), list(miss_analy.missRate.values), align = 'center',color=['red','green','yellow','steelblue'])
  7. plt.title('Histogram of missing value of variables')
  8. plt.xlabel('variables names')
  9. plt.ylabel('missing rate')
  10. # 添加x轴标签，并旋转90度
  11. plt.xticks(np.arange(miss_analy.shape[0]),list(miss_analy['index']))
  12. pl.xticks(rotation=90)
  13. # 添加数值显示
  14. for x,y in enumerate(list(miss_analy.missRate.values)):
  15.     plt.text(x,y+0.12,'{:.2%}'.format(y),ha='center',rotation=90)    
  16. plt.ylim([0,1.2])
  18. plt.show()

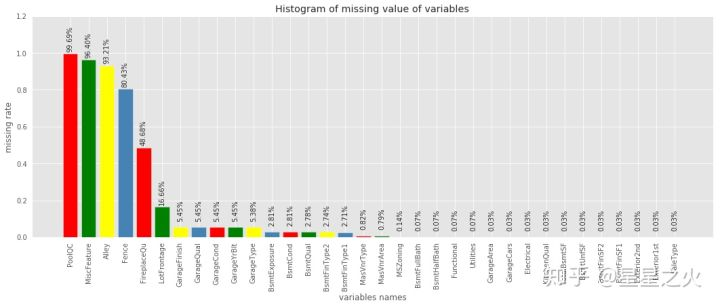缺失值处理3 - 图6这样的统计计算以及可视化基本已经看出哪些变量缺失，以及缺失比例情况，对数据即有个缺失概况。下面将对缺失变量进行相应处理。

2、缺失处理

方式1：删除

直接去除含有缺失值的记录，这种处理方式是简单粗暴的，适用于数据量较大（记录较多）且缺失比较较小的情形，去掉后对总体影响不大。一般不建议这样做，因为很可能会造成数据丢失、数据偏移。

  1. func: df.dropna(axis=0, how='any', thresh=None, subset=None, inplace=False)
  3. # 1、删除‘age’列
  4. df.drop('age', axis=1, inplace=True)
  6. # 2、删除数据表中含有空值的行
  7. df.dropna()
  9. # 3、丢弃某几列有缺失值的行
  10. df.dropna(axis=0, subset=['a','b'], inplace=True)

直接去除缺失变量，基于第一步我们已经知道每个变量的缺失比例，如果一个变量的缺失比例过高，基本也就失去了预测意义，这样的变量我们可以尝试把它直接去掉。

  1. # 去掉缺失比例大于80%以上的变量
  2. data=data.dropna(thresh=len(data)*0.2, axis=1)

方式2：常量填充

在进行缺失值填充之前，我们要先对缺失的变量进行业务上的了解，即变量的含义、获取方式、计算逻辑，以便知道该变量为什么会出现缺失值、缺失值代表什么含义。比如，‘age’ 年龄缺失，每个人均有年龄，缺失应该为随机的缺失，‘loanNum’贷款笔数，缺失可能代表无贷款，是有实在意义的缺失。全局常量填充：可以用0，均值、中位数、众数等填充。平均值适用于近似正态分布数据，观测值较为均匀散布均值周围；中位数适用于偏态分布或者有离群点数据，中位数是更好地代表数据中心趋势；众数一般用于类别变量，无大小、先后顺序之分。

  1. # 均值填充
  2. data['col'] = data['col'].fillna(data['col'].means())
  3. # 中位数填充
  4. data['col'] = data['col'].fillna(data['col'].median())
  5. # 众数填充
  6. data['col'] = data['col'].fillna(stats.mode(data['col'])[0][0])

也可以借助Imputer类处理缺失:

  1. from sklearn.preprocessing import Imputer
  2. imr = Imputer(missing_values='NaN', strategy='mean', axis=0)
  3. imputed_data =pd.DataFrame(imr.fit_transform(df.values),columns=df.columns)
  4. imputed_data

方式3：插值填充

采用某种插入模式进行填充，比如取缺失值前后值的均值进行填充：

  1. #  interpolate()插值法，缺失值前后数值的均值，但是若缺失值前后也存在缺失，则不进行计算插补。
  2. df['a'] = df['a'].interpolate()
  4. # 用前面的值替换, 当第一行有缺失值时，该行利用向前替换无值可取，仍缺失
  5. df.fillna(method='pad')
  7. # 用后面的值替换，当最后一行有缺失值时，该行利用向后替换无值可取，仍缺失
  8. df.fillna(method='backfill')#用后面的值替换

方式4：KNN填充

利用knn算法填充，其实是把目标列当做目标标量，利用非缺失的数据进行knn算法拟合，最后对目标列缺失进行预测。（对于连续特征一般是加权平均，对于离散特征一般是加权投票）

fancyimpute 类**

  1. from fancyimpute import KNN
  2. fill_knn = KNN(k=3).fit_transform(data)
  3. data = pd.DataFrame(fill_knn)

sklearn类

  1. from sklearn.neighbors import KNeighborsClassifier, KNeighborsRegressor
  3. def knn_filled_func(x_train, y_train, test, k = 3, dispersed = True):
  4.     # params: x_train 为目标列不含缺失值的数据（不包括目标列）
  5.     # params: y_train 为不含缺失值的目标列
  6.     # params: test 为目标列为缺失值的数据（不包括目标列）
  7.     if dispersed:
  8.         knn= KNeighborsClassifier(n_neighbors = k, weights = "distance")
  9.     else:
  10.         knn= KNeighborsRegressor(n_neighbors = k, weights = "distance")
  12.     knn.fit(x_train, y_train)
  13.     return test.index, knn.predict(test)

方式5：随机森林填充

随机森林算法填充的思想和knn填充是类似的，即利用已有数据拟合模型，对缺失变量进行预测。

  1. from sklearn.ensemble import RandomForestRegressor, RandomForestClassifier
  3. def knn_filled_func(x_train, y_train, test, k = 3, dispersed = True):
  4.     # params: x_train 为目标列不含缺失值的数据（不包括目标列）
  5.     # params: y_train 为不含缺失值的目标列
  6.     # params: test 为目标列为缺失值的数据（不包括目标列）
  7.     if dispersed:
  8.         rf= RandomForestRegressor()
  9.     else:
  10.         rf= RandomForestClassifier()
  12.     rf.fit(x_train, y_train)
  13.     return test.index, rf.predict(test)

3、缺失衍生

有时候，可以根据某个字段是否缺失，进行新变量的衍生，比如，”信用卡数量”，若该字段缺失，代表’无信用卡’，则可以根据”信用卡数量”是否缺失衍生’有无信用卡’字段，这种衍生很可能是很有效果的。

4、总结

总之，处理缺失值是需要研究数据规律与缺失情况来进行处理的，复杂的算法不一定有好的效果，因此，还要具体问题具体分析，尤其是要搞明白字段含义以及缺失意义，这往往容易被忽略。个人经验，数据处理需要去探索，没有一成不变的万全之策。