一、什么是回归
“回归”是由英国著名生物学家兼统计学家高尔顿(Francis Galton,1822~1911.生物学家达尔文的表弟)在研究人类遗传问题时提出来的。19世纪高斯系统地提出最小二乘估计,从而使回归分析得到蓬勃发展。
目前回归分析的研究范围划分如下图:
二、常见的回归算法
| 函数名称 | 算法名称 | |
|---|---|---|
| LinearRegression | 线性回归 | |
| SVR | 支持向量回归 | |
| KNeighborsRegressor | 最近邻回归 | |
| GaussianProcessRegressor | 高斯过程回归 | |
| DecisionTreeRegressor | 决策树回归 | |
| RandomForestRegressor | 随机森林回归 | |
| AdaBoostRegressor | AdaBoost回归 | |
| GradientBoostingRegressor | 梯度提升树GBDT回归 | |
| XGBRegressor | XGBoost回归 | |
| LGBMRegressor | LightGBM回归 | |
三、常见的回归模型评价
- 误差、解释方差分、r2
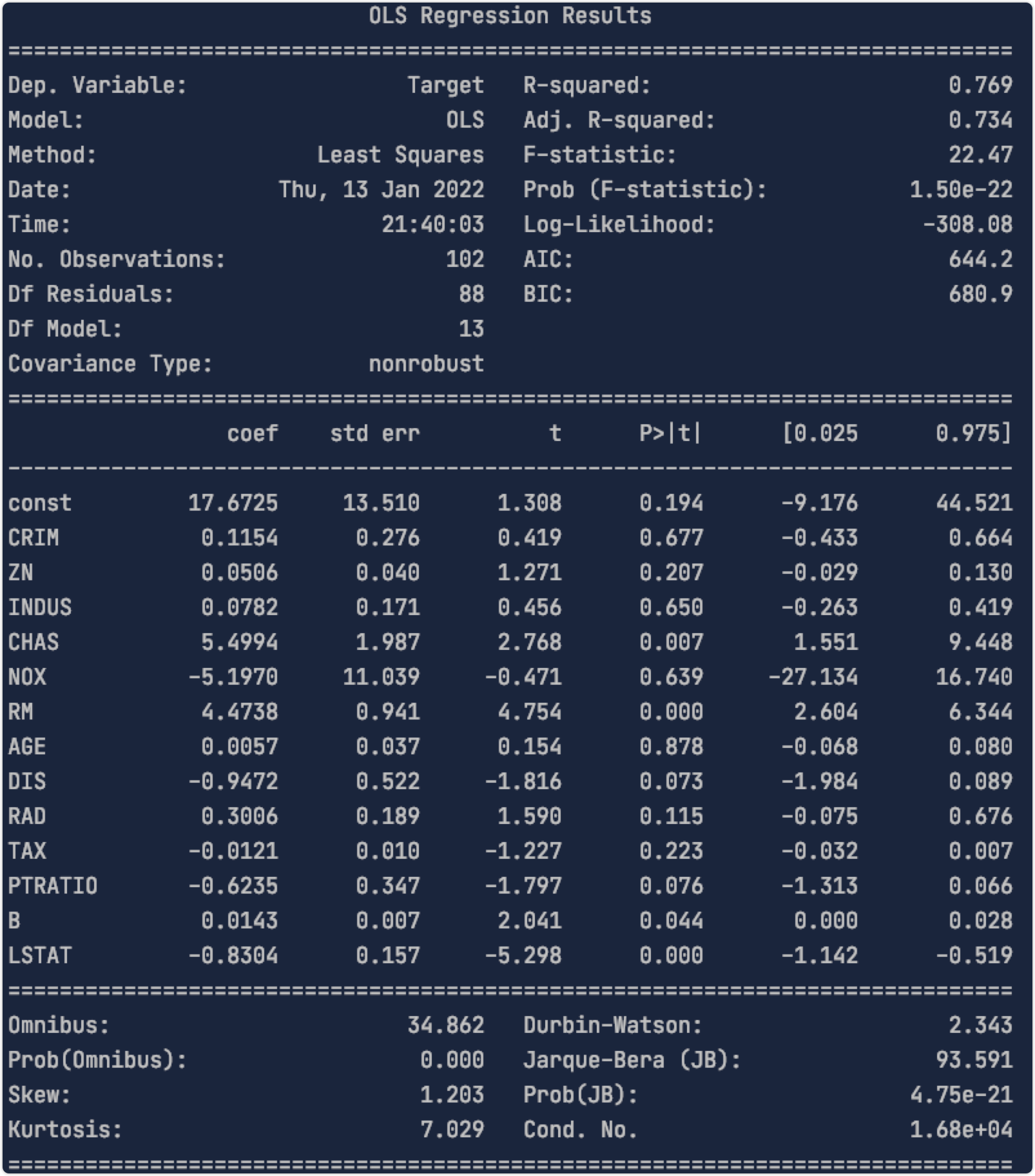
- OLS回归分析报告
- 假设检验p值
# 线性回归模型评估# 1、均方误差、平均绝对误差、中位数绝对误差、解释方差分、r2from sklearn.metrics import mean_squared_error, mean_absolute_percentage_error, median_absolute_error, explained_variance_score, r2_scoreprint("mean_squared_error:", mean_squared_error(y_pred=y_pred_2, y_true=y_test))print("mean_absolute_percentage_error:", mean_absolute_percentage_error(y_pred=y_pred_2, y_true=y_test))print("median_absolute_error:", median_absolute_error(y_pred=y_pred_2, y_true=y_test))print("explained_variance_score:", explained_variance_score(y_pred=y_pred_2, y_true=y_test))print("r2_score:", r2_score(y_pred=y_pred_2, y_true=y_test))# 2、OLS回归分析报告import statsmodels.api as sm# 将特征变量x_test添加常数项,赋值给x2x2 = sm.add_constant(x_test)# 对y_test和x2,用OLS()最小二乘法,进行线性回归方程搭建est = sm.OLS(y_test, x2).fit()# 打印该模型的数据信息print(est.summary())# R-squared越接近1,模型拟合程度越高。# Adj. R-squared是R-squared的改进版。# p值小于0.05,认为与目标变量有显著相关性。# 3、假设检验p值from scipy import statsrvs1 = stats.norm.rvs(loc=5, scale=10, size=500)rvs2 = stats.norm.rvs(loc=5, scale=10, size=500)print(stats.ttest_ind(rvs1, rvs2))
6.1 模型自评估表格
6.1.1 模型选择:
【LinearRegression;GradientBoostingRegressor;XGBRegressor;RandomForestRegressor】
| 模型 | 简介 |
|---|---|
| LinearRegression | 利用最小二乘函数对一个或多个自变量之间关系进行建模 |
| RandomForestRegressor | 利用多个决策树对样本进行训练、分类并预测的一种算法 |
| GradientBoostingRegressor | GBDT是一个加性回归模型,通过boosting迭代的构造一组弱学习器,相对LR的优势如不需要做特征归一化,自动进行选择可解释性较低的模型,可以适应多种损失函数如Square Loss,Log Loss等。 |
| XGBRegressor | xgboost扩展和改进了GDBT,xgboost算法更快,准确率也相对高一些。 |
6.1.2 评估指标:
6.1.2.1 RMSE(均方根误差):
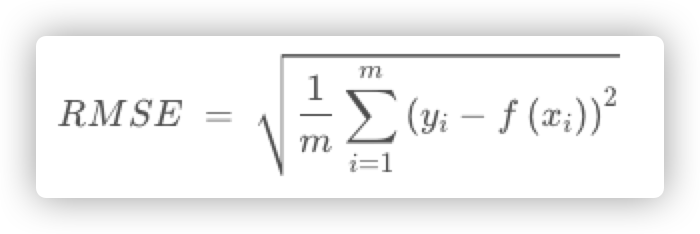
均方根误差就是在均方误差的基础上再开方,其值越小说明拟合效果越好。
6.1.2.2 MAE(平均绝对误差):
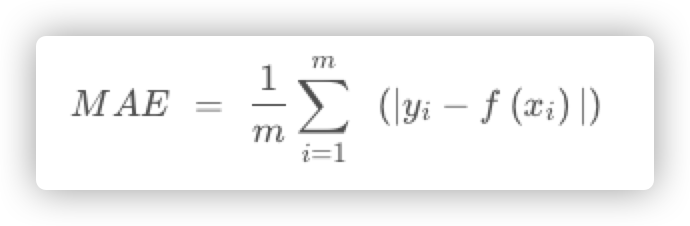
计算每一个样本的预测值和真实值的差的绝对值,然后求和再取平均值。用于评估预测结果和真实数据集的接近程度,其值越小说明拟合效果越好。
6.1.2.3 MAD(中位数绝对误差):
先计算出数据与它们的中位数之间的残差(偏差),MAD就是这些偏差的绝对值的中位数。
绝对中位数MAD是对单变量数值型数据的样本偏差的一种鲁棒性测量。同时也可以表示由样本的MAD估计得出的总体参数,其值越小说明拟合效果越好。。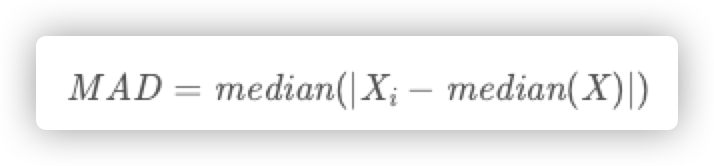
6.1.2.4 解释方差分:
y(i)为真实值,f(xi)为预测值,var为方差
解释方差的最大值是1.0,数值越大代表模型预测结果越好,越小代表模型预测结果越差
6.1.2.5 决定系数(R2)
它可以看作是MSE的标准化版本,用于更好地解释模型的性能,代表了模型拟合的效果。
SST反映了真实的y的方差。决定系数R2反映了y的波动有多少百分比能被X的波动所描述,R2的取值范围0~1。然后使用MSE定义R2,
在y变化越剧烈(Var(y)很大)的时候(即大方差)情况下,预测的也很好(MSE会小)的话,则说明模型越好!说明模型对多样性数据的拟合能力比较强!
从另一个角度思考,y的方差越小,说明很相似很集中,当然就更容易拟合
6.1.2.6 模型综合评估
在度量一个回归模型的好坏时,会同时采用残差图、均方根误差RMSE和决定系数R2。
1)残差图可以更直观地掌握每个样本的误差分布。
2)均方根误差RMSE的值越小越好,但是不考虑样本本身的分布。
3)R2综合考虑了测试样本本身波动的分布性。