参考资料：

机器学习中的缺失值处理1（机器学习理论若干问题）

数据值缺失是数据分析中经常遇到的问题之一。当缺失比例很小时，可直接对缺失记录进行舍弃或进行手工处理。但在实际数据中，往往缺失数据占有相当的比重。这时如果手工处理非常低效，如果舍弃缺失记录，则会丢失大量信息，使不完全观测数据与完全观测数据间产生系统差异，对这样的数据进行分析，很可能会得出错误的结论。

1 造成数据缺失的原因

  • 信息被遗漏，可能是因为输入时认为不重要、忘记填写了或对数据理解错误而遗漏，也可能是由于数据采集设备的故障、存储介质的故障、传输媒体的故障、一些人为因素等原因而丢失。
  • 信息暂时无法获取。例如在医疗数据库中，并非所有病人的所有临床检验结果都能在给定的时间内得到，就致使一部分属性值空缺出来
  • 获取这些信息的代价太大。

对缺失值的处理要具体问题具体分析，属性缺失有时并不意味着数据缺失，缺失本身是包含信息的，所以需要根据不同应用场景下缺失值可能包含的信息进行合理填充。

2 缺失的类型

将数据集中不含缺失值的变量称为完全变量，数据集中含有缺失值的变量称为不完全变量。从缺失的分布来将缺失可以分为完全随机缺失，随机缺失和完全非随机缺失。

  • 完全随机缺失（missing completely at random,MCAR）：指的是数据的缺失是完全随机的，不依赖于任何不完全变量或完全变量，不影响样本的无偏性。如家庭地址缺失。
  • 随机缺失(missing at random,MAR)：指的是数据的缺失不是完全随机的，即该类数据的缺失依赖于其他完全变量。例如财务数据缺失情况与企业的大小有关。
  • 非随机缺失(missing not at random,MNAR)：指的是数据的缺失与不完全变量自身的取值有关。如高收入人群的不原意提供家庭收入。

随机缺失可以通过已知变量对缺失值进行估计；而非随机缺失还没有很好的解决办法。

3 缺失值处理的方法

缺失值处理主要有三种主要方法：删除元组、数据补齐、不处理

3.1 删除元组

存在遗漏信息属性值的对象（元组，记录）删除，从而得到一个完备的信息表，在对象有多个属性缺失值、被删除的含缺失值的对象与初始数据集的数据量相比非常小的情况下非常有效

优点：快速，不需要任何先验知识；
缺点：它以减少历史数据来换取信息的完备，会丢弃大量隐藏在这些对象中的信息

3.2 数据补齐

这类方法是用一定的值去填充空值，从而使信息表完备化。
常用的方法如下：

（1）人工填写（filling manually）
由于最了解数据的还是用户自己，因此这个方法产生数据偏离最小，可能是填充效果最好的一种。然而一般来说，该方法很费时，当数据规模很大、空值很多的时候，该方法是不可行的。
（2）特殊值填充（Treating Missing Attribute values as Special values）
将空值作为一种特殊的属性值来处理，它不同于其他的任何属性值。如所有的空值都用“unknown”填充。这样将形成另一个有趣的概念，可能导致严重的数据偏离，一般不推荐使用。
（3）平均值填充（Mean/Mode Completer）
将初始数据集中的属性分为数值属性和非数值属性来分别进行处理。
如果空值是数值型的，就根据该属性在其他所有对象的取值的平均值来填充该缺失的属性值；
如果空值是非数值型的，就根据统计学中的众数原理，用该属性在其他所有对象的取值次数最多的值(即出现频率最高的值)来补齐该缺失的属性值。
（4）条件平均值填充法（Conditional Mean Completer）
在该方法中，用于求平均的值并不是从数据集的所有对象中取，而是从与该对象具有相同决策属性值的对象中取得。
  • 热卡填充（Hot deck imputation，或就近补齐）
    对于一个包含空值的对象，热卡填充法在完整数据中找到一个与它最相似的对象，然后用这个相似对象的值来进行填充。不同的问题可能会选用不同的标准来对相似进行判定。该方法概念上很简单，且利用了数据间的关系来进行空值估计。这个方法的缺点在于难以定义相似标准，主观因素较多。
（4）K最近距离邻法（K-means clustering）
先根据欧式距离或相关分析来确定距离具有缺失数据样本最近的K个样本，将这K个值加权平均来估计该样本的缺失数据。
（5）回归（Regression）
基于完整的数据集，建立回归方程。对于包含空值的对象，将已知属性值代入方程来估计未知属性值，以此估计值来进行填充。当变量不是线性相关时会导致有偏差的估计。
（6）期望值最大化方法（Expectation maximization，EM）
EM算法是一种在不完全数据情况下计算极大似然估计或者后验分布的迭代算法。在每一迭代循环过程中交替执行两个步骤：E步（Excepctaion step,期望步），在给定完全数据和前一次迭代所得到的参数估计的情况下计算完全数据对应的对数似然函数的条件期望；M步（Maximzation step，极大化步），用极大化对数似然函数以确定参数的值，并用于下步的迭代。算法在E步和M步之间不断迭代直至收敛，即两次迭代之间的参数变化小于一个预先给定的阈值时结束。该方法可能会陷入局部极值，收敛速度也不是很快，并且计算很复杂。
（6）C4.5方法
通过寻找属性间的关系来对遗失值填充。它寻找之间具有最大相关性的两个属性，其中没有遗失值的一个称为代理属性，另一个称为原始属性，用代理属性决定原始属性中的遗失值。这种基于规则归纳的方法只能处理基数较小的名词型属性。

（7）随机森林填充缺失值

4 不处理

补齐处理只是将未知值补以我们的主观估计值，不一定完全符合客观事实，在对不完备信息进行补齐处理的同时，我们或多或少地改变了原始的信息系统。而且，对空值不正确的填充往往将新的噪声引入数据中，使挖掘任务产生错误的结果。因此，在许多情况下，我们还是希望在保持原始信息不发生变化的前提下对信息系统进行处理。

主要有以下几种方法：

  • 贝叶斯网络
  • 人工神经网络
  • 把变量映射到高维空间
    比如性别，有男、女、缺失三种情况，则映射成3个变量：是否男、是否女、是否缺失。连续型变量也可以这样处理。比如Google、百度的CTR预估模型，预处理时会把所有变量都这样处理，达到几亿维。这样做的好处是完整保留了原始数据的全部信息、不用考虑缺失值、不用考虑线性不可分之类的问题。缺点是计算量大大提升

5 总结

总的来说，处理缺失值的主要方法如下：

  • 使用可用特征的均值来填补缺失值
  • 使用特殊值来填补缺失值
  • 忽略有缺失值的样本
  • 使用相似样本的均值填补缺失值
  • 使用另外的机器学习算法预测缺失值

6 实际操作

当我们拿到一批数据的时候，往往都是“不干净”的，而缺失值是最常见也是最容易发现的。不同的缺失值处理方式对接下来的特征提取，建模等都有巨大影响。那么缺失值的处理是有一套流程的：

6.1 发现缺失值

  1. 统计每个特征在所有个体中缺失的个数 / 缺失率

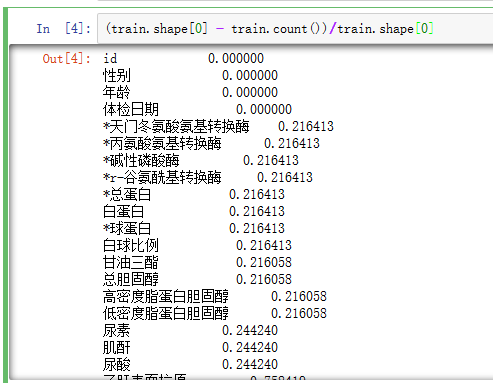
这一点是查找缺失的特征
pandas 中 count() 函数为不为空数据的个数，那么将shape与count做差就得到缺失个数，缺失率。

  1. (df.shape[0] - df.count())/df.shape[0]

缺失值处理1 - 图1

  1. 对于每个个体所缺失的特征个数

这一点是查找缺失的个体
这个简单，对数据 df 转置一下即可

  1. (df.shape[1] - df.T.count())/df.shape[1]
  1. pandas 其他缺失值函数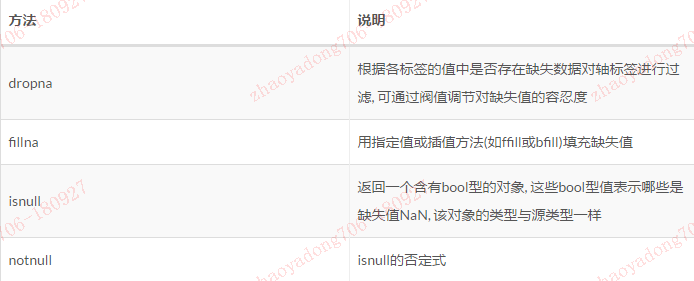
    缺失值处理1 - 图2
  2. 隐藏的缺失值
    这里要理解数据集内容的含义，比如在某些情况下，0代表缺失值。因为有些值为0的变量是无意义的，可以表示为缺失值。例如：身高、体重等。

6.2 缺失机制

在对缺失数据进行处理前，了解数据缺失的机制和形式是十分必要的。将数据集中不含缺失值的变量（属性）称为完全变量，数据集中含有缺失值的变量称为不完全变量，Little 和 Rubin定义了以下三种不同的数据缺失机制：

  • 完全随机缺失（Missing Completely at Random，MCAR）。数据的缺失与不完全变量以及完全变量都是无关的。
  • 随机缺失（Missing at Random，MAR）。数据的缺失仅仅依赖于完全变量。
  • 非随机、不可忽略缺失（Not Missing at Random,NMAR，or nonignorable）。不完全变量中数据的缺失依赖于不完全变量本身，这种缺失是不可忽略的。

从缺失值的所属属性上讲，如果所有的缺失值都是同一属性，那么这种缺失成为单值缺失，如果缺失值属于不同的属性，称为任意缺失。另外对于时间序列类的数据，可能存在随着时间的缺失，这种缺失称为单调缺失。

6.3 空值语义

对于某个对象的属性值未知的情况，我们称它在该属性的取值为空值(null value)。空值的来源有许多种，因此现实世界中的空值语义也比较复杂。总的说来，可以把空值分成以下三类：

  1. 不存在型空值。即无法填入的值，或称对象在该属性上无法取值，如一个未婚者的配偶姓名等。
  2. 存在型空值。即对象在该属性上取值是存在的，但暂时无法知道。一旦对象在该属性上的实际值被确知以后，人们就可以用相应的实际值来取代原来的空值，使信息趋于完全。存在型空值是不确定性的一种表征，该类空值的实际值在当前是未知的。但它有确定性的一面，诸如它的实际值确实存在，总是落在一个人们可以确定的区间内。一般情况下，空值是指存在型空值。
  3. 占位型空值。即无法确定是不存在型空值还是存在型空值，这要随着时间的推移才能够清楚，是最不确定的一类。这种空值除填充空位外，并不代表任何其他信息。

6.4 判断缺失值的重要性

对于包含有缺失值处理的算法，比如XGB或者LGB，我们可以简单的直接把训练数据扔到模型中训练，查看feature_importance。（由于XGB等属于树模型，不需要太多的数据预处理过程，比如归一化等，也能取得较好的效果，且模型参数对特征的重要性程度影响不是很大，我们只需要知道大概的结果，哪些重要，哪些不重要即可）

6.5 缺失值较多且不重要的特征

这些特征我们看情况，可以尝试着直接删除，如果不删除，缺失值又多，处理不好，可能会引来噪声。

至于为什么看情况呢，意思是，做个对比试验，一组是删除的，另一组是没删除的，进行交叉验证，如果删除后的结果比较好，那么就进行删除。

6.6 缺失值较少的特征

6.6.1 统计量填充

  • 这一类特征，我们可以简单使用统计量比如：均值、中位数、众数 进行填充；
  • 对于连续值，推荐使用 中位数 ，可以排除一些特别大或者特别小的异常值造成的影响；
  • 对于离散值，推荐使用 众数 ，均值和中位数用不了吧，那就用众数好了。。。
  1. df = df.fillna(df.median(axis=0))

6.6.2 特殊值填充

我们可以填一个不在正常取值范围内的数值，比如 -999 ，0 等来表示缺失值。

  1. df.fillna(-999)

6.6.3 不处理

大家可能都有一个疑惑，为什么对很多人说XGB或者LGB对缺失值不敏感呢，当用缺失值的训练XGB时，算法不会报错，其实这个不能叫不敏感，而是算法本身自己有一套缺失值处理算法，比如XGB，它会把含有缺失值的数据分别分到左右两个子节点，然后计算着两种情况的损失，最后，选取较好的划分结果和对应的损失。

所以，如果遇到有缺失值的情况，最好还是根据缺失的情况，自己处理比较好。

6.6.4 分类别填充

我们还可以根据label的类别，取值范围进行更高级的统计量填充（当然这个只适用于知道label的训练集），即取在该label下数据的中位数、均值等进行填充。

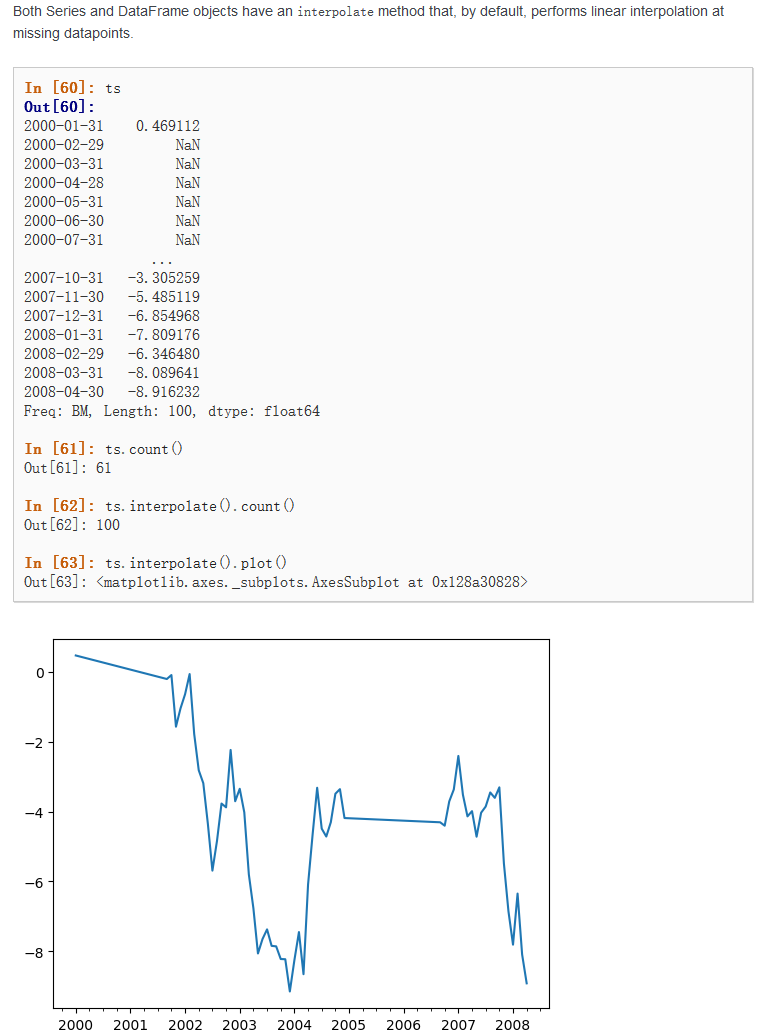
6.6.5 插值填充

使用线性，多项式等差值方法，对于时间序列的缺失问题，可以使用此方法。

  1. df.interpolate()

缺失值处理1 - 图3

6.6.6 插补法

  1. 随机插补法——从总体中随机抽取某个样本代替缺失样本
  2. 多重插补法——通过变量之间的关系对缺失数据进行预测，利用蒙特卡洛方法生成多个完整的数据集，在对这些数据集进行分析，最后对分析结果进行汇总处理
  3. 热平台插补——指在非缺失数据集中找到一个与缺失值所在样本相似的样本（匹配样本），利用其中的观测值对缺失值进行插补
    优点：简单易行，准去率较高
    缺点：变量数量较多时，通常很难找到与需要插补样本完全相同的样本。但我们可以按照某些变量将数据分层，在层中对缺失值实用均值插补
  4. 拉格朗日差值法和牛顿插值法

6.6.7 用预测值填充

将缺失的数据当成label，没缺失的作为训练集，缺失的作为测试集，通过某种机器学习算法进行预测，填补缺失值。下面代码以lgb为例：

  1. import lightgbm as lgb
  2. def set_missing(df, predict_list):
  3.     for predict_feature in predict_list:
  4.         # 原始数据分为已知和未知的
  5.         known = df[df[predict_feature].notnull()]
  6.         unknown = df[df[predict_feature].isnull()]
  7.         # 训练集构造，从已知的部分构造
  8.         y = known[predict_feature].as_matrix()
  9.         X = known.drop(predict_feature, axis=1).as_matrix()
  10.         # 测试集，从未知的部分构造
  11.         test_X = unknown.drop(predict_feature, axis=1).as_matrix()
  12.         # 用lgb模型进行训练
  13.         predicted_feature = _model_predict(X, y, test_X)
  14.         # 用得到的预测结果填补原缺失数据
  15.         df.loc[(df[predict_feature].isnull()), predict_feature] = predicted_feature
  16.     return df
  17. def _model_predict(X, y, test_X):
  18.     from sklearn.model_selection import train_test_split
  19.     X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1)
  20.     lgb_train = lgb.Dataset(X_train, y_train)
  21.     lgb_eval = lgb.Dataset(X_test, y_test, reference=lgb_train)
  22.     params = {
  23.         'boosting': 'gbdt',
  24.         'objective': 'regression',
  25.         'metric': 'rmse',
  26.         'num_leaves': 31,
  27.         'min_data_in_leaf': 20,
  28.         'learning_rate': 0.015,
  29.         'cat_smooth': 10,
  30.         'feature_fraction': 0.8,
  31.         'bagging_freq': 5,
  32.         'verbosity': 0
  33.     }
  34.     gbm = lgb.train(params,
  35.                     lgb_train,
  36.                     num_boost_round=1000,
  37.                     valid_sets=lgb_eval,
  38.                     early_stopping_rounds=70)
  39.     # 用得到的模型进行未知年龄结果预测
  40.     predicted_feature = gbm.predict(test_X, num_iteration=gbm.best_iteration)
  41.     print("---------best_iteration: ", gbm.best_iteration)
  42.     return predicted_feature

6.7 缺失值比较多的样本

当样本很多的时候，而缺失值比较多的样本，且它们数目不多时，直接删掉。

6.8 随机森林处理缺失值

  1. import pandas as pd
  2. import matplotlib.pyplot as plt
  3. import numpy as np
  4. from  sklearn.ensemble import RandomForestClassifier
  5. df=pd.read_csv('E:\\Users\\Administrator\\Desktop\\pythonNotebook\\train.csv',index_col=0)
  6. data=df[['Survived', 'Pclass', 'Sex', 'Age', 'SibSp', 'Parch','Fare', 'Cabin', 'Embarked']]
  7. #更改分类变量对应的值
  8. data.loc[data['Sex']=='male','Sex']=0
  9. data.loc[data['Sex']=='female','Sex']=1
  10. #同理，更改Embarked对应的值
  11. data.loc[data['Embarked']=='S','Embarked']=0
  12. data.loc[data['Embarked']=='C','Embarked']=1
  13. data.loc[data['Embarked']=='Q','Embarked']=2
  14. te=data[data['Embarked'].notnull()]#非空的embarked对应的行
  15. te_X=te[['Survived','Pclass','Sex','SibSp','Parch','Fare']]#设定输入的X
  16. te_Y=te[['Embarked']]#设定输入的Y
  17. te_X=te_X.astype(float)#转换数据类型，不转换成数值型的，到后面输入模型会报错。
  18. te_Y=te_Y.astype(float)#转换数据类型，不转换成数值型的，到后面输入模型会报错。
  19. tr=data[data['Embarked'].isnull()]
  20. tr_X=tr[['Survived','Pclass','Sex','SibSp','Parch','Fare']].astype(float)
  21. tr_Y=tr['Embarked'].astype(float)
  22. fc=RandomForestClassifier()
  23. fc.fit(te_X,te_Y)
  24. pr=fc.predict(tr_X)
  26. data[data['Embarked'].isnull(),'Embarked']=pr#将预测的缺失值补充到原来的缺失的位置

这里只是简单的举例，利用随机森林（可以是RandomForestClassifier,RandomForestRegressor,这里用的是前者）去补充缺失值。同理也可以对age数据补充，这里就要用到RandomForestRegressor了，相应的前面应该是from sklearn.ensemble import RandomForestRegressor。如果有提示报错的话，还是要看看数据类型的有没有弄错。

随机森林，指的是利用多棵树对样本进行训练并预测的一种分类器。该分类器最早由Leo Breiman和Adele Cutler提出。简单来说，是一种bagging的思想，采用bootstrap，生成多棵树，CART（Classification And Regression Tree）构成的。对于每棵树，它们使用的训练集是从总的训练集中有放回采样出来的，这意味着，总的训练集中的有些样本可能多次出现在一棵树的训练集中，也可能从未出现在一棵树的训练集中。对于一个有n行的数据集，out of bag 的概率大概是1/e＝1/3。n趋向无穷大的时候，(1-1/n)^n～1/e。

1-随机森林算法特色

  1. 在与其它现有的算法相比，其预测准确率很好
  2. 在较大的数据集上计算速度依然很快
  3. 不需要降维，算法本身是采取随机降维的
  4. 他能处理有缺失值的数据集。算法内部有补缺失值的函数
  5. 能给出变量的重要性
  6. 能处理imbalanced data set
  7. 能给出观测实例间的相似度矩阵，其实就是proximity啦，继而能做clustering 和 location outlier
  8. 能对unlabeled data 进行无监督的学习，进行clustering
  9. 生成的森林可以保留，应用在新的数据集上
    最重要的是1-6。7-9我并没找到很有说服力的例子能证明随机森林在这几方面也很强。

2-根据其特色说一说随机森林算法

随机森林是如何补全缺失值的

前提：训练数据集中label（被解释变量）一定要有，不然这条观测实例你为何拿他来学习模型？

randomForest包里，有两种补全缺失值的方法。

方法一（na.roughfix）简单粗暴，对于训练集,同一个class下的数据，如果是分类变量缺失，用众数补上，如果是连续型变量缺失，用中位数补。

方法二（rfImpute）这个方法计算量大，至于比方法一好坏？不好判断。他只能补训练集中的缺失值。是先用na.roughfix补上缺失值，然后构建森林并计算proximity matrix，再回头看缺失值，如果是分类变量，则用没有缺失的观测实例的proximity中的权重进行投票。如果是连续型变量，则用proximity矩阵进行加权平均的方法补缺失值。然后迭代4-5次。这个补缺失值的思想和KNN有些类似。

对于7，proximity matrix

前面的rfImpute就是基于proximity matrix的，proximity matrix其实就是任意两个观测实例间的相似度矩阵。原理是如果两个观测实例落在同一棵树的同一个叶子节点的次数越多，则这两个观测实例的相似度越高。这个矩阵进行了归一化，就是除以ntree

对于5.能给出变量的重要性

无非就是进行feature selection，降低模型的复杂度的同时获取较好的预测准确率。