参考资料：
常用聚类度量指标
sklearn聚类性能度量：main
轮廓系数及可视化中心点

聚类算法内部度量：

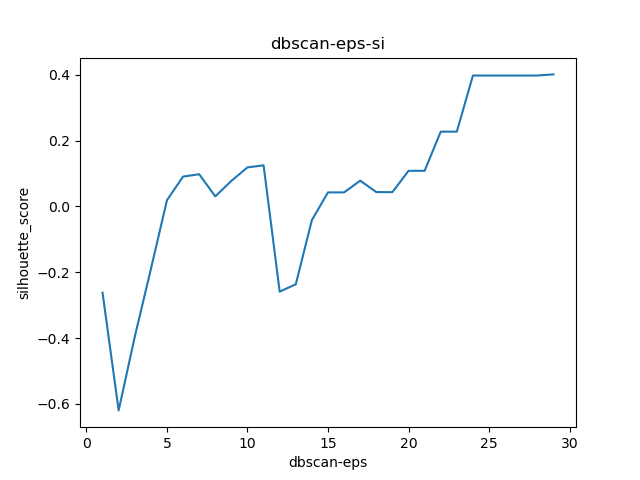
1. 轮廓系数（Silhouette Coefficient）

函数：
def silhouette_score(X, labels, metric=‘euclidean’, sample_size=None,
random_state=None, **kwds)：

函数值说明：
所有样本的s i 的均值称为聚类结果的轮廓系数，定义为S，是该聚类是否合理、有效的度量。聚类结果的轮廓系数的取值在【-1,1】之间，值越大，说明同类样本相距约近，不同样本相距越远，则聚类效果越好。

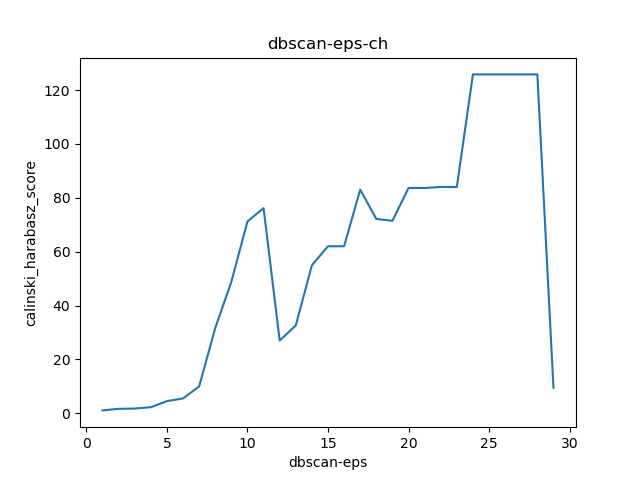
2. CH分数（Calinski Harabasz Score ）

函数：
def calinski_harabasz_score(X, labels):
函数值说明：
类别内部数据的协方差越小越好，类别之间的协方差越大越好，这样的Calinski-Harabasz分数会高。 总结起来一句话：CH index的数值越大越好。

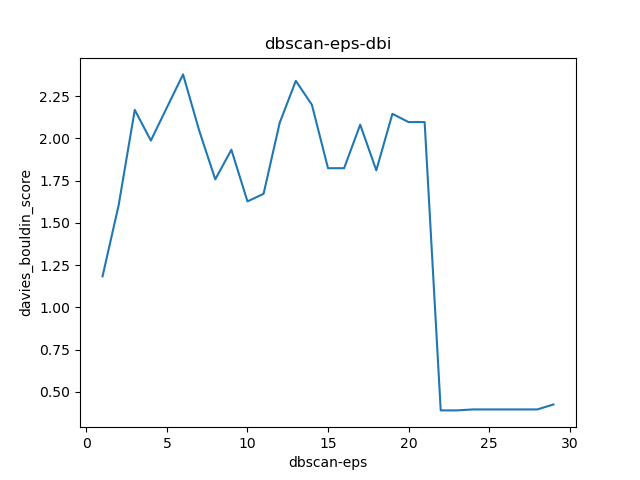
3. 戴维森堡丁指数(DBI)——davies_bouldin_score

函数：
def davies_bouldin_score(X, labels):
函数值说明：
注意：DBI的值最小是0，值越小，代表聚类效果越好。

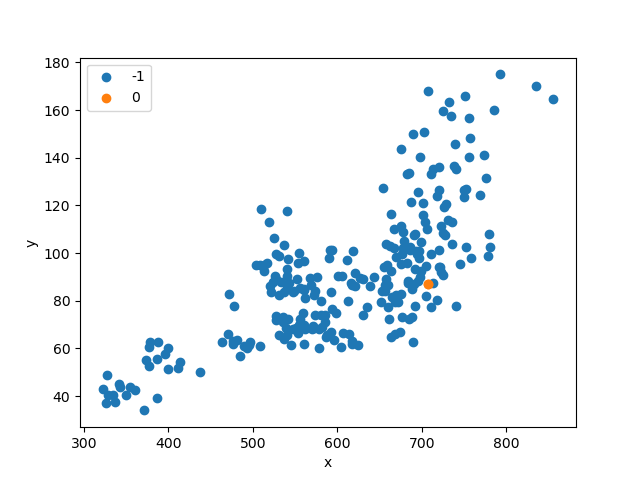
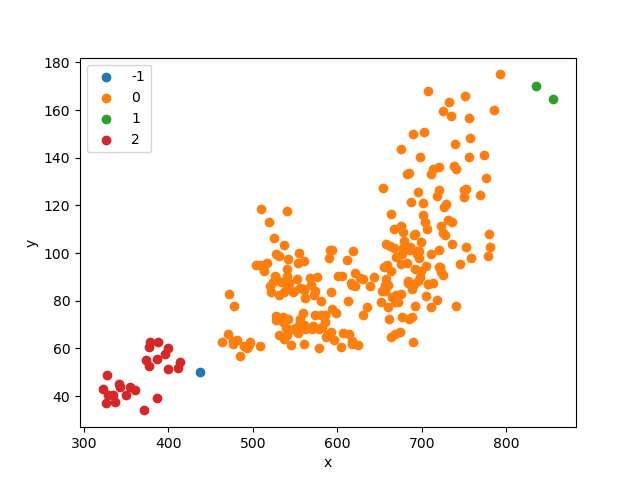
  1. import pandas as pd
  2. from numpy import unique
  3. from numpy import where
  4. from matplotlib import pyplot
  5. from sklearn import metrics
  6. from sklearn.cluster import DBSCAN
  7. import matplotlib.pyplot as plt
  9. data = pd.read_excel('cluster_data.xlsx')
  10. eps_list = []
  11. si_list = []
  12. ch_list = []
  13. dbi_list = []
  15. """
  16. 聚类-内部度量
  17. Calinski-Harabaz Index：
  19. 在scikit-learn中， Calinski-Harabasz Index对应的方法是metrics.calinski_harabaz_score.
  20. CH指标通过计算类中各点与类中心的距离平方和来度量类内的紧密度，通过计算各类中心点与数据集中心点距离平方和来度量数据集的分离度，CH指标由分离度与紧密度的比值得到。从而，CH越大代表着类自身越紧密，类与类之间越分散，即更优的聚类结果。
  22. sklearn.metrics.silhouette_score:轮廓系数
  24. silhouette_sample
  25. 对于一个样本点(b - a)/max(a, b)
  26. a平均类内距离，b样本点到与其最近的非此类的距离。
  27. silihouette_score返回的是所有样本的该值,取值范围为[-1,1]。
  29. 这些度量均是越大越好
  30. """
  31. # 初始参数聚类
  32. model = DBSCAN(min_samples=2)
  33. # 模型拟合与聚类预测
  34. X = data[['x', 'y']].values
  35. yhat = model.fit_predict(X)
  36. # 检索唯一群集
  37. clusters = unique(yhat)
  38. # 为每个群集的样本创建散点图
  39. for cluster in clusters:
  40.     # 获取此群集的示例的行索引
  41.     row_ix = where(yhat == cluster)
  42.     # 创建这些样本的散布
  43.     pyplot.scatter(X[row_ix, 0], X[row_ix, 1], label=cluster)
  44. # 绘制散点图
  45. pyplot.xlabel('x')
  46. pyplot.ylabel('y')
  47. plt.legend()
  48. pyplot.show()
  50. eps_cal = 1
  51. while eps_cal < 30:
  52.     model = DBSCAN(eps=eps_cal, min_samples=2)
  53.     label_list = model.fit_predict(data)
  54.     # 轮廓系数
  55.     cluster_score_si = metrics.silhouette_score(data, label_list)
  57.     cluster_score_ch = metrics.calinski_harabasz_score(data, label_list)
  59.     # DBI的值最小是0，值越小，代表聚类效果越好。
  60.     cluster_score_DBI = metrics.davies_bouldin_score(data, label_list)
  62.     eps_list.append(eps_cal)
  63.     si_list.append(cluster_score_si)
  64.     ch_list.append(cluster_score_ch)
  65.     dbi_list.append(cluster_score_DBI)
  66.     eps_cal += 1
  68. plt.figure()
  69. plt.plot(eps_list, si_list)
  70. plt.xlabel("dbscan-eps")
  71. plt.ylabel("silhouette_score")
  72. plt.title("dbscan-eps-si")
  73. plt.show()
  75. plt.figure()
  76. plt.plot(eps_list, ch_list)
  77. plt.xlabel("dbscan-eps")
  78. plt.ylabel("calinski_harabasz_score")
  79. plt.title("dbscan-eps-ch")
  80. plt.show()
  82. plt.figure()
  83. plt.plot(eps_list, dbi_list)
  84. plt.xlabel("dbscan-eps")
  85. plt.ylabel("davies_bouldin_score")
  86. plt.title("dbscan-eps-dbi")
  87. plt.show()
  89. # eps经过参数调优，选择22为合适值
  90. model = DBSCAN(eps=22, min_samples=2)
  91. # 模型拟合与聚类预测
  92. X = data[['x', 'y']].values
  93. yhat = model.fit_predict(X)
  94. # 检索唯一群集
  95. clusters = unique(yhat)
  96. # 为每个群集的样本创建散点图
  97. for cluster in clusters:
  98.     # 获取此群集的示例的行索引
  99.     row_ix = where(yhat == cluster)
  100.     # 创建这些样本的散布
  101.     pyplot.scatter(X[row_ix, 0], X[row_ix, 1], label=cluster)
  102. # 绘制散点图
  103. pyplot.xlabel('x')
  104. pyplot.ylabel('y')
  105. plt.legend()
  106. pyplot.show()

image.pngimage.pngimage.pngimage.pngimage.png

数据及代码

https://github.com/SeafyLiang/machine_learning_study/blob/master/cluster/cluster_measure.py