通常在拿到一份数据进行相关的模型训练之前，我们需要进行数据清洗以便得到干净的数据。进一步需要找到与问题有关的特征信息，并把这些特征转换成特征矩阵的数值，这也就是机器学习实践中的重要步骤之一，特征工程。

本文章将从数据特征的分布分析、对比分析、统计分析、贡献度分析(帕累托分析)、和特征的相关性分析来识别数据集整体上的一些重要性质。

一、分布分析

1.1 理论介绍

分布分析是用来解释数据的分布类型和分布特征，显示其分布情况。所以可以对一开始拿到数据可以首先进行初步的分布分析。分布分析主要分成两种：

①对定量的数据进行分布分析
②对定性的数据进行分布分析。

①对定量数据的分布分析按照如下步骤进行：
1、求极差 2、决定组距与组数 3、决定分点 4、绘制频率分布图

②对定性的数据分布分析：
根据变量的分类类型来确定分组，然后使用图形对信息进行显示。

1.2 二手房数据分析案例

比如现在你爬取到某地区的二手房信息数据，针对这一批数据的房价你要做一次定量分布分析，以及对不同房子的朝向做一个定性的分布分析，以便初步的了解房子的一些特征分布。

1.2.1 参考房价定量分析

1.首先利用pandas读取数据并取前五条数据得到如下信息。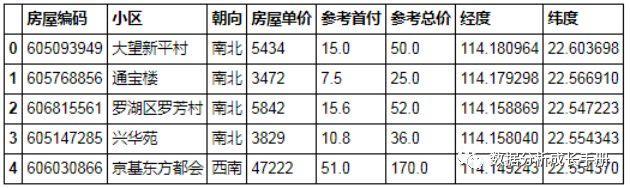

2.求参考总价的分组区间并在原始数据中添加一个新的字段“参考总价分组区间”。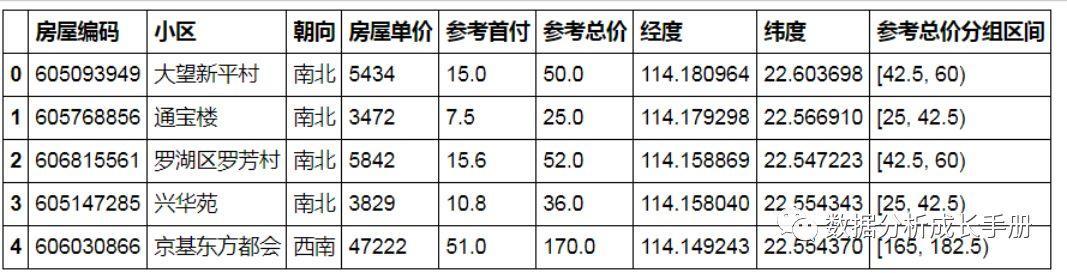

3.计算每段参考总价的区间的频数、频率并绘制直方图。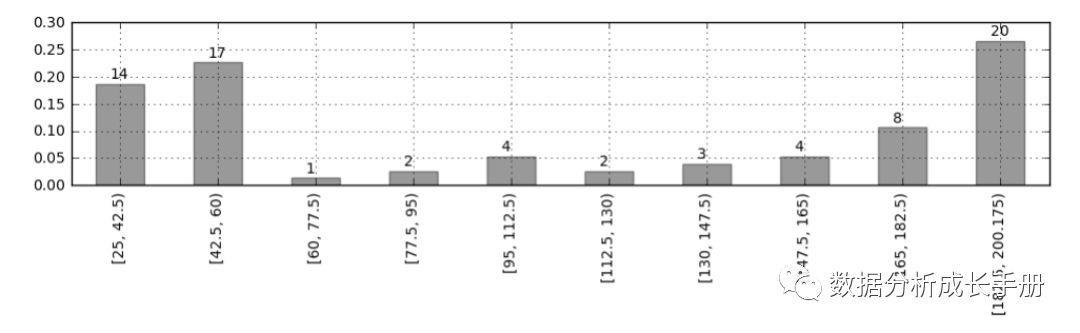

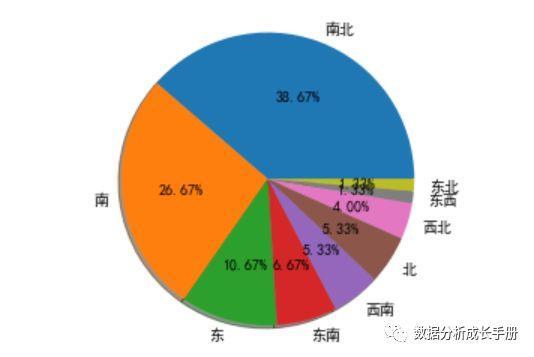
1.2.2 房屋朝向定性分析

对不同房屋朝向占比可绘制一个饼图。

二、对比分析

2.1 理论介绍

对比分析是指把两个相互联系的指标进行比较，从数量上展示和说明研究对象规模的大小、水平的高低、速度的快慢，以及各种关系是否协调。特别适用于指标间的横纵向比较、时间序列的比较分析。在对比分析中，选择合适的对比标准是十分关键的步骤，选择合适，才能做出客观的评价，选择不合适，评价可能得出错误的结论。

对比分析主要分为以下两种形式：

1. 绝对数比较
   利用这组指标绝对数进行对比，从而寻找差异的一种方法。
2. 相对数比较
   它是由两个有联系的指标对比计算的，用以反映客观现象之间数量联系程度的综合指标，其数值表现为相对数。由于研究目的和对比基础不用，相对数可以分为以下几种：结构相对数、比例相对数、动态相对数和空间相对数

2.2 产品销量数据分析案例

2.2.1 绝对数比较案例

比如现在有某公司的A、B产品某月销量数据，这里我们可以对A、B产品的销量做绝对数对比。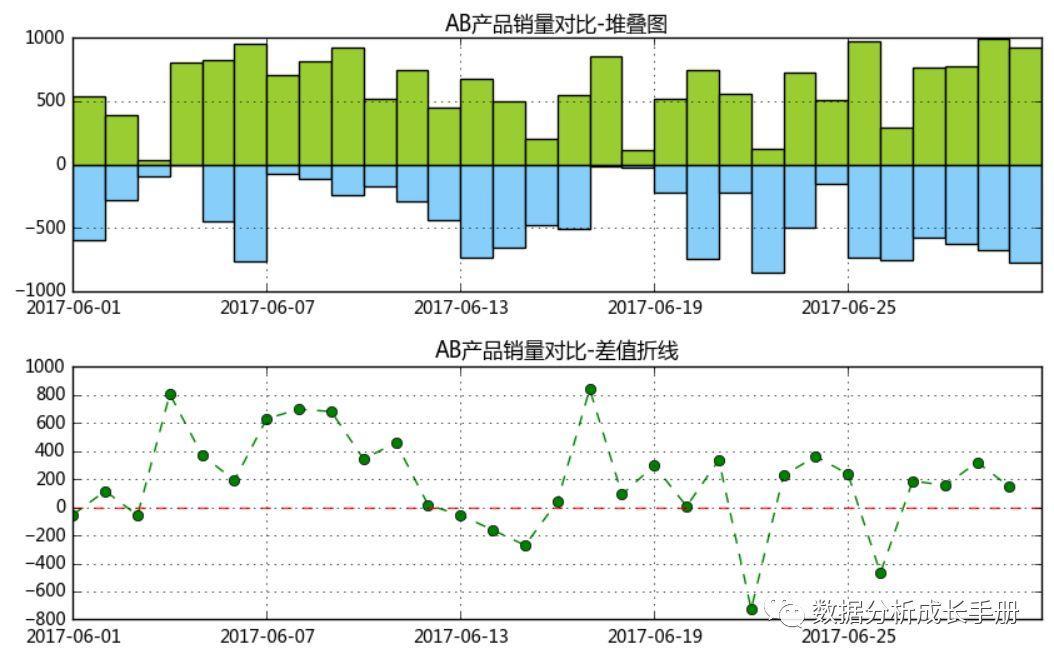

2.2.2 相对数比较案例：

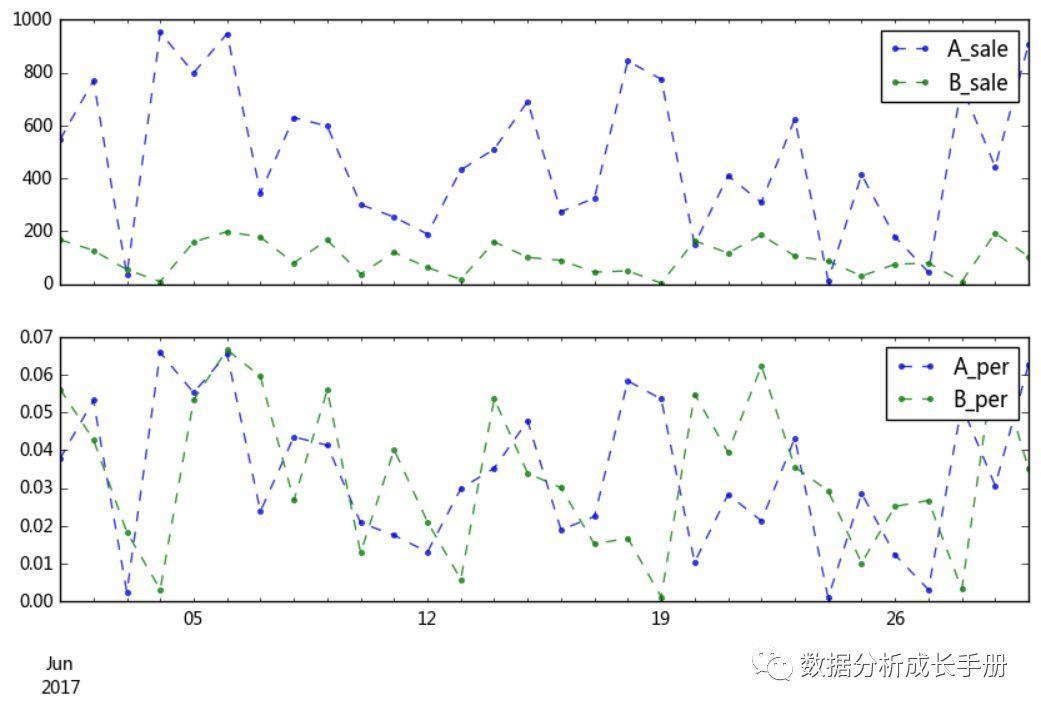
• 结构相对数：在分组基础上，各组总量指标与总体的总量指标对比，计算出各组数量在总量中所占比重。例如，30天内A、B产品的日销售额，由于 A、B产品销售额量级不同，计算出A、B产品每日销售额占该月各自总销售额对比。

• 比例相对数：比例相对数 = 总体中某一部分数值 / 总体中另一部分数值 。如 “基本建设投资额中工业、农业、教育投资的比例”、“男女比例”
• 空间相对数（横向）：比如说同样的2017年北京和深圳膜拜单车使用量，空间是比较抽象的更多的是在时间相同的情况下，不同的元素的比较 。

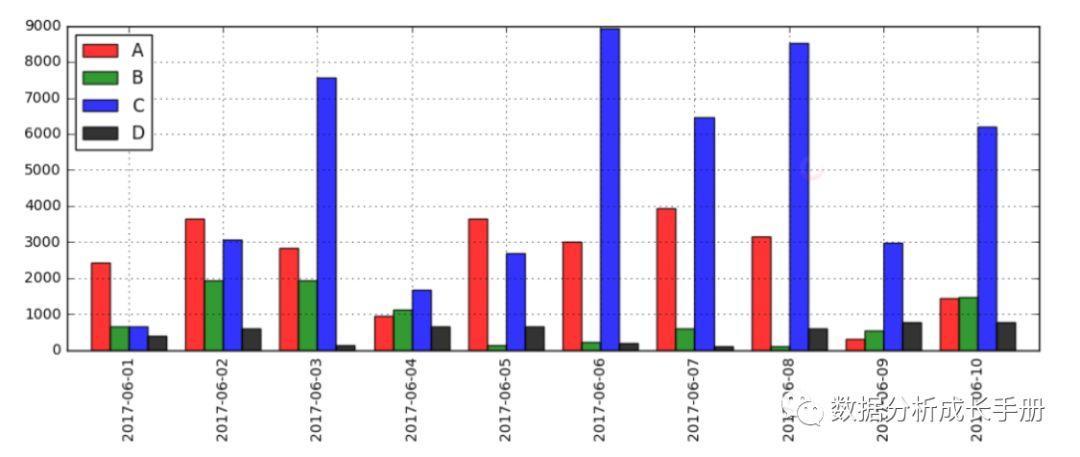
• 动态相对数（纵向）：将同一现象在不同时期的指标数值对比，用以说明发展方向和变化的速度，如发展速度、增长速度等。例如求A产品的某月的定基增长速度额环比增长速度

三、统计分析

3.1 理论介绍

对一组数据用统计指标定量的分析数据，一般从集中趋势和离中趋势两个方面来衡量数据。

1. 数据的集中趋势：指一组数据向某一中心靠拢的倾向，核心在于寻找数据的代表值或中心值 ，所以需要找到数据的统计平均数来衡量。统计平均数可分为，①算术平均数、加权算术平均数②位置平均数。
2. 数据的离中趋势：指一组数据中各数据以不同程度的距离偏离中心的趋势，可用极差与分位差、方差与标准差、离散系数 等衡量。

3.2 数据分析案例：

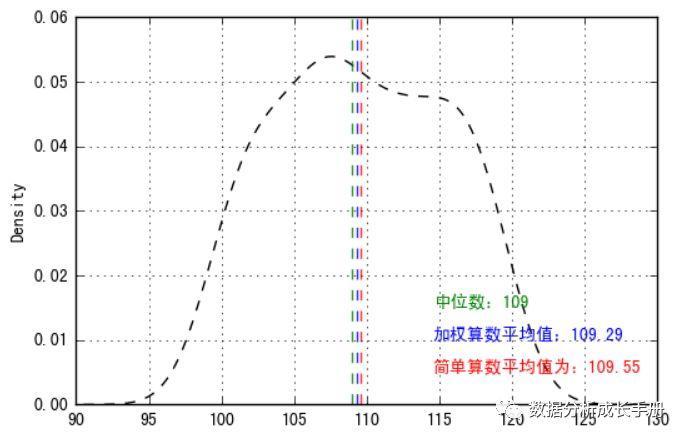
对某一组数据分析其集中趋势结果：

对某一组数据分析其离中趋势结果：
你要比较A、B数据的分散程度，可求得其分位差和其他指标。你可以绘制箱型图对比。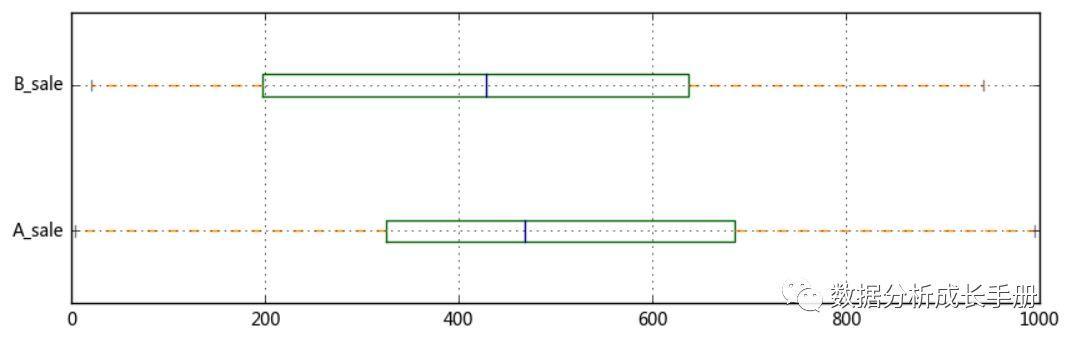

四、帕累托分析

4.1 理论介绍

帕累托分析又叫贡献度分析，原理是20/80定律，即80%的利润常常来自于20%的产品。一般来说投入产出，努力和报酬之间并不是绝对的线性关系，总有一些关键因素起着至关重要的作用，而帕累托分析就是找到影响事务的关键因素，分清主次。

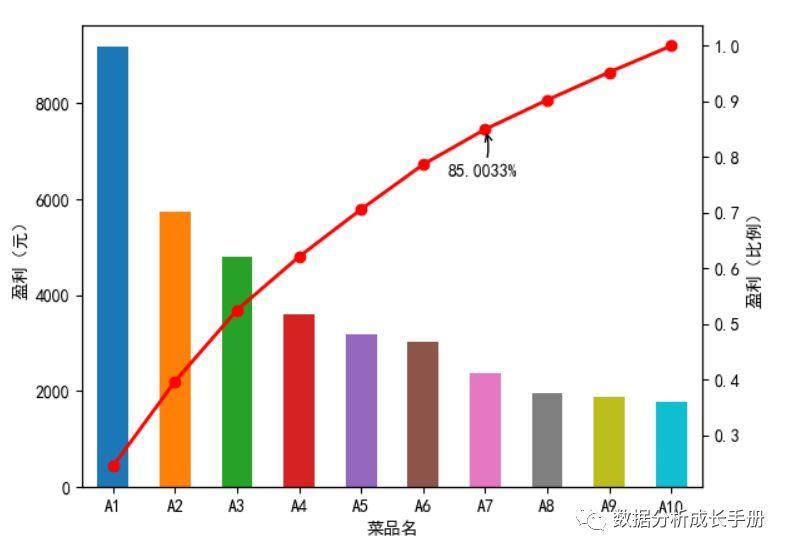
4.2 餐厅数据分析案例

例如现在你有一份餐厅的不同菜品的盈利数据，你想找到哪些菜对该菜厅的盈利贡献最大。可按照如下步骤来实现贡献度分析：

1. 对不同菜品按盈利额排序
2. 计算累积占比
3. 找到累积占比85%的菜品，并找到其对应的索引位置。
4. 绘制盈利图并标记核心位置。

五、相关性分析

详细内容：
数据挖掘01-相关性分析及可视化【Pearson, Spearman, Kendall】

5.1 理论介绍

相关性分析是研究两个或两个以上处于同等地位的随机变量间的相关关系的统计分析方法。例如，人的身高和体重之间；空气中的相对湿度与降雨量之间的相关关系都是相关分析研究的问题。

相关分析与回归分析之间的区别：回归分析侧重于研究随机变量间的依赖关系，以便用一个变量去预测另一个变量;相关分析侧重于发现随机变量间的种种相关特性。可用相关系数r来衡量两个特征之间的相关性。

相关系数r的解读：

1. 正相关：如果x,y变化的方向一致，如登陆次数和商机用户的关系，r>0；一般地， |r|>0.95 存在显著性相关|r|≥0.8 高度相关；0.5≤|r|<0.8 中度相关0.3≤|r|<0.5 低度相关；|r|<0.3 关系极弱，认为不相关。
2. 负相关：如果x,y变化的方向相反，如吸烟与肺功能的关系，r<0
3. 无线性相关：r=0。

关于相关系数的计算有三种：
①Pearson相关系数
②Spearman秩相关系数
③Kendall相关系数。

注意点：皮尔逊相关系数的计算是数据分布为正态分布，所以计算之前要先进行正态性检验。对于不服从正太分布变量的关联性可用斯皮尔曼相关系数来计算，也叫等级相关系数。

5.2 pandas数据分析案例

1. 首先对数据进行正太性检验，利用scipy里面集成好的K-S检验方法。

2. 利用pandas里面集成好的相关系数计算方法。

总结：本文对数据特征的一些常用分析方法进行了系统介绍，并利用Python里面的科学计算库Numpy、Pandas、Scipy、Matplotlib实现了每一种分析方法的分析结果，并且将结果图形化显示出来。