超参数调优方法：网格搜索（GridSearch），随机搜索（RandomSearch），贝叶斯优化（BO）等算法。

参考资料：三种超参数优化方法详解，以及代码实现

实验基础代码

  1. import numpy as np
  2. import pandas as pd
  3. from lightgbm.sklearn import LGBMRegressor
  4. from sklearn.metrics import mean_squared_error
  5. import warnings
  7. warnings.filterwarnings('ignore')
  8. from sklearn.datasets import load_diabetes
  9. from sklearn.model_selection import KFold, cross_val_score
  10. from sklearn.model_selection import train_test_split
  11. import timeit
  12. import os
  13. import psutil
  15. # 在sklearn.datasets的糖尿病数据集上演示和比较不同的算法，加载它。
  16. diabetes = load_diabetes()
  17. data = diabetes.data
  18. targets = diabetes.target
  19. n = data.shape[0]
  20. random_state = 42
  21. # 时间占用 s
  22. start = timeit.default_timer()
  23. # 内存占用 mb
  24. info_start = psutil.Process(os.getpid()).memory_info().rss / 1024 / 1024
  25. train_data, test_data, train_targets, test_targets = train_test_split(data, targets,
  26.                                                                       test_size=0.20, shuffle=True,
  27.                                                                       random_state=random_state)
  28. num_folds = 2
  29. kf = KFold(n_splits=num_folds, random_state=random_state, shuffle=True)
  30. model = LGBMRegressor(random_state=random_state)
  31. score = -cross_val_score(model, train_data, train_targets, cv=kf, scoring="neg_mean_squared_error", n_jobs=-1).mean()
  32. print('score：', score)
  34. end = timeit.default_timer()
  35. info_end = psutil.Process(os.getpid()).memory_info().rss / 1024 / 1024
  37. print('此程序运行占内存' + str(info_end - info_start) + 'mB')
  38. print('Running time:%.5fs' % (end - start))

实验结果为：
最小平方误差：3897.5550693355276
此程序运行占内存0.5mB
Running time:1.48060s

出于对比目的，我们将优化仅调整以下三个参数的模型：
n_estimators：从100到2000
max_depth：2到20
learning_rate：从10e-5到1

一、网格搜索（GridSearch）

网格搜索可能是最简单，应用最广泛的超参数搜索算法，他通过查找搜索范围内的所以的点来确定最优值。如果采用较大的搜索范围及较小的步长，网格搜索很大概率找到全局最优值。然而这种搜索方案十分消耗计算资源和时间，特别是需要调优的超参数比较多的时候。
因此在实际应用过程中，网格搜索法一般会先使用较广的搜索范围和较大的步长，来找到全局最优值可能的位置；然后再缩小搜索范围和步长，来寻找更精确的最优值。这种操作方案可以降低所需的时间和计算量，但由于目标函数一般是非凸的，所以很可能会错过全局最优值。
网格搜素对应于sklearn中的GridSearchCV模块:sklearn.model_selection.GridSearchCV
(estimator, param_grid, , scoring=None, n_jobs=None, iid=’deprecated’, refit=True, cv=None, verbose=0, pre_dispatch=’2n_jobs’, error_score=nan, return_train_score=False). 详情见博客。

1.1 GridSearch算法代码

  1. from sklearn.model_selection import GridSearchCV
  2. # 时间占用 s
  3. start = timeit.default_timer()
  4. # 内存占用 mb
  5. info_start = psutil.Process(os.getpid()).memory_info().rss / 1024 / 1024
  7. param_grid = {'learning_rate': np.logspace(-3, -1, 3),
  8.               'max_depth': np.linspace(5, 12, 8, dtype=int),
  9.               'n_estimators': np.linspace(800, 1200, 5, dtype=int),
  10.               'random_state': [random_state]}
  11. gs = GridSearchCV(model, param_grid, scoring='neg_mean_squared_error',
  12.                   n_jobs=-1, cv=kf, verbose=False)
  13. gs.fit(train_data, train_targets)
  14. gs_test_score = mean_squared_error(test_targets, gs.predict(test_data))
  16. end = timeit.default_timer()
  17. info_end = psutil.Process(os.getpid()).memory_info().rss / 1024 / 1024
  19. print('此程序运行占内存' + str(info_end - info_start) + 'mB')
  20. print('Running time:%.5fs' % (end - start))
  21. print("Best MSE {:.3f} params {}".format(-gs.best_score_, gs.best_params_))

实验结果：
此程序运行占内存12.79296875mB
Running time:6.35033s
Best MSE 3696.133 params {‘learning_rate’: 0.01, ‘max_depth’: 5, ‘n_estimators’: 800, ‘random_state’: 42}

1.2 可视化解释

  1. import matplotlib.pyplot as plt
  2. gs_results_df = pd.DataFrame(np.transpose([-gs.cv_results_['mean_test_score'],
  3.                                            gs.cv_results_['param_learning_rate'].data,
  4.                                            gs.cv_results_['param_max_depth'].data,
  5.                                            gs.cv_results_['param_n_estimators'].data]),
  6.                              columns=['score', 'learning_rate', 'max_depth',
  7.                                       'n_estimators'])
  8. gs_results_df.plot(subplots=True, figsize=(10, 10))
  9. plt.show()

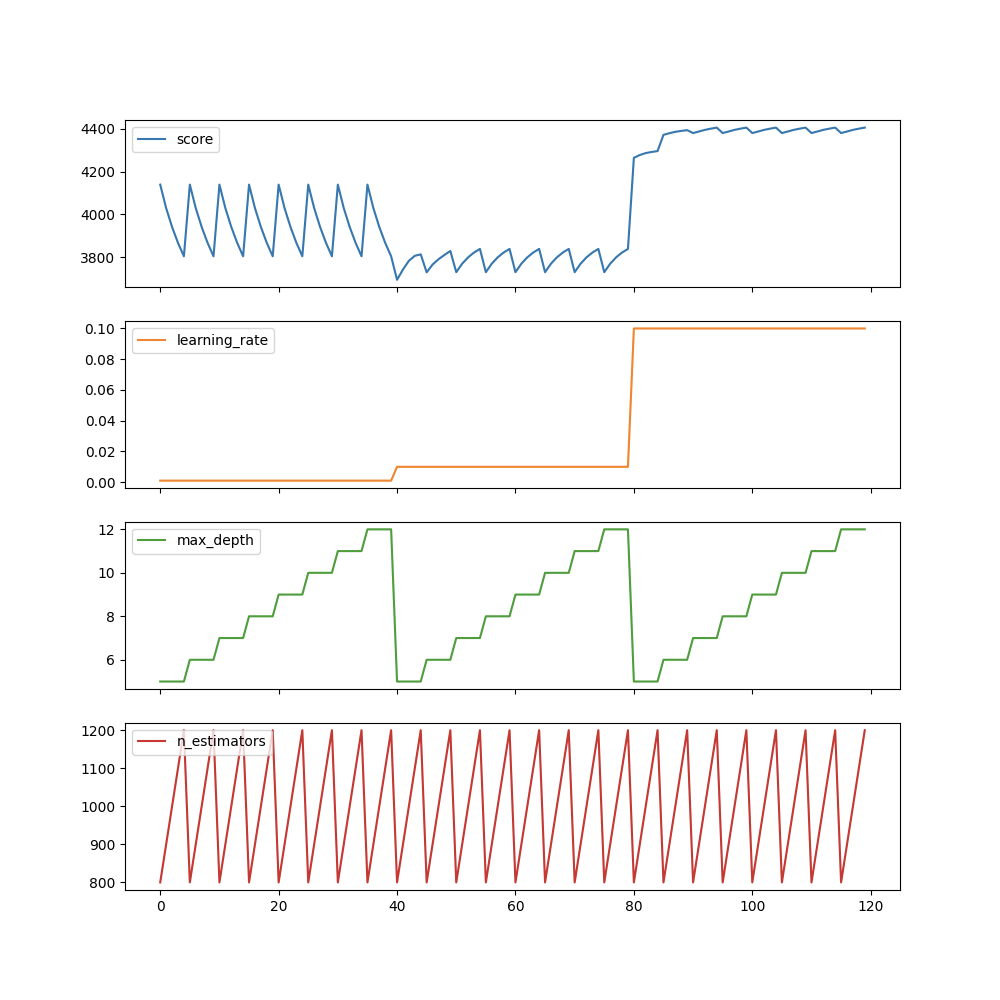
image.png
我们可以看到，例如max_depth是最不重要的参数，它不会显着影响得分。 但是，我们正在搜索max_depth的8个不同值，并且在其他参数上搜索了任何固定值。 显然浪费时间和资源。

二、随机搜索（RandomSearch）

https://www.cnblogs.com/cgmcoding/p/13634531.html
随机搜索的思想与网络搜索比较相似，只是不再测试上界和下界之间所有值，而是在搜索范围内随机选取样本点。他的理论依据是，如果样本点集足够大，那么通过随机采样也能大概率地找到全局最优值或近似值。随机搜索一般会比网络搜索要快一些。我们在搜索超参数的时候，如果超参数个数较少（三四个或者更少），那么我们可以采用网格搜索，一种穷尽式的搜索方法。但是当超参数个数比较多的时候，我们仍然采用网格搜索，那么搜索所需时间将会指数级上升。
　 所以有人就提出了随机搜索的方法，随机在超参数空间中搜索几十几百个点，其中就有可能有比较小的值。这种做法比上面稀疏化网格的做法快，而且实验证明，随机搜索法结果比稀疏网格法稍好。RandomizedSearchCV使用方法和类GridSearchCV 很相似，但他不是尝试所有可能的组合，而是通过选择每一个超参数的一个随机值的特定数量的随机组合，这个方法有两个优点：
如果你让随机搜索运行， 比如1000次，它会探索每个超参数的1000个不同的值（而不是像网格搜索那样，只搜索每个超参数的几个值）
你可以方便的通过设定搜索次数，控制超参数搜索的计算量。
　　RandomizedSearchCV的使用方法其实是和GridSearchCV一致的，但它以随机在参数空间中采样的方式代替了GridSearchCV对于参数的网格搜索，在对于有连续变量的参数时，RandomizedSearchCV会将其当做一个分布进行采样进行这是网格搜索做不到的，它的搜索能力取决于设定的niter参数，同样的给出代码。
image.png
随机搜索对于于sklearn中的sklearn.model_selection.RandomizedSearchCV
（_estimator，param_distributions，*，n_iter = 10，得分= None，n_jobs = None，iid =’deprecated’，refit = True，cv = None，verbose = 0，pre_dispatch =’2 * n_jobs’，random_state = None，error_score = nan，return_train_score = False ）参数与GridSearchCV大致相同，但是多了一个n_iter,为迭代轮数。

  1. from sklearn.model_selection import RandomizedSearchCV
  2. from scipy.stats import randint
  4. param_grid_rand = {'learning_rate': np.logspace(-5, 0, 100),
  5.                    'max_depth': randint(2, 20),
  6.                    'n_estimators': randint(100, 2000),
  7.                    'random_state': [random_state]}
  8. # 时间占用 s
  9. start = timeit.default_timer()
  10. # 内存占用 mb
  11. info_start = psutil.Process(os.getpid()).memory_info().rss / 1024 / 1024
  12. rs = RandomizedSearchCV(model, param_grid_rand, n_iter=50, scoring='neg_mean_squared_error',
  13.                         n_jobs=-1, cv=kf, verbose=False, random_state=random_state)
  15. rs.fit(train_data, train_targets)
  17. rs_test_score = mean_squared_error(test_targets, rs.predict(test_data))
  18. end = timeit.default_timer()
  19. info_end = psutil.Process(os.getpid()).memory_info().rss / 1024 / 1024
  21. print('此程序运行占内存' + str(info_end - info_start) + 'mB')
  22. print('Running time:%.5fs' % (end - start))
  23. print("Best MSE {:.3f} params {}".format(-rs.best_score_, rs.best_params_))

此程序运行占内存17.90625mB
Running time:3.85010s
Best MSE 3516.383 params {‘learning_rate’: 0.0047508101621027985, ‘max_depth’: 19, ‘n_estimators’: 829, ‘random_state’: 42}

由此可见在运行50轮的时候效果已经比GridSearchCV效果要好了，而且用时更短。

三、贝叶斯优化（BO）

  1.   网格搜索速度慢，但在搜索整个搜索空间方面效果很好，而随机搜索很快，但可能会错过搜索空间中的重要点。幸运的是，还有第三种选择：贝叶斯优化。本文我们将重点介绍贝叶斯优化的一个实现，一个名为hyperopt的 Python 模块。贝叶斯优化算法在寻找最优和最值参数时。采用了与网格搜索和随机搜索完全不同的方法。网格搜素和随机搜索在测试一个新点时，会忽略前一个点的信息，而贝叶斯优化算法则充分利用了之前的信息。贝叶斯优化算法通过对目标函数形状进行学习，找到使目标函数向全局最优值提升的参数。<br />      具体来说，学习目标函数的方法是，首先根据先验分布，假设一个搜索函数；然后，每一次使用新的采样点来测试目标函数时，利用这个信息来更新目标函数的先验分布；最后，算法测试由后验分布给出的全局最值可能出现的位置的点。对于贝叶斯优化算法，有一个需要注意的是，一旦找到可一个局部最优值，他会在该区域不断采样，所以很容易陷入局部最优值。为了弥补这个缺点，贝叶斯算法会在探索和利用之间找到一个平衡点，探索就是在还未取样的区域获取采样点，而利用则根据后验分布在最可能出现的全局最值区域进行采样。<br />      我们将使用[hyperopt库](http://hyperopt.github.io/hyperopt/#documentation)来处理此算法。 它是超参数优化最受欢迎的库之一。详细介绍看博客。<br />(1)TPE算法：<br /> algo=tpe.suggest<br />TPE是Hyperopt的默认算法。 它使用贝叶斯方法进行优化。 它在每一步都试图建立函数的概率模型，并为下一步选择最有希望的参数。 这类算法的工作方式如下：
  1. 生成随机初始点x
  2. 计算F(x)
  3. 利用试验历史尝试建立条件概率模型P(F|x)
  4. 根据P(F|x)选择xi最有可能导致更好的F(xi)
  5. 计算F(xi)的实际值

  6. 重复步骤3-5，直到满足停止条件之一，例如i>max_evals ```python from hyperopt import fmin, tpe, hp, anneal, Trials def gb_mse_cv(params, random_state=random_state, cv=kf, X=train_data, y=train_targets):

    the function gets a set of variable parameters in “param”

    params = {‘n_estimators’: int(params[‘n_estimators’]), 

    1.        'max_depth': int(params['max_depth']), 
    2.       'learning_rate': params['learning_rate']}

    we use this params to create a new LGBM Regressor

    model = LGBMRegressor(random_state=random_state, **params)

    and then conduct the cross validation with the same folds as before

    score = -cross_val_score(model, X, y, cv=cv, scoring=”neg_mean_squared_error”, n_jobs=-1).mean()

    return score

    状态空间，最小化函数的params的取值范围

    space={‘n_estimators’: hp.quniform(‘n_estimators’, 100, 2000, 1),

    1. 'max_depth' : hp.quniform('max_depth', 2, 20, 1),
    2. 'learning_rate': hp.loguniform('learning_rate', -5, 0)

    }

trials 会记录一些信息

trials = Trials()

时间占用 s

start=timeit.default_timer()

内存占用 mb

info_start = psutil.Process(os.getpid()).memory_info().rss/1024/1024 best=fmin(fn=gb_mse_cv, # function to optimize space=space, algo=tpe.suggest, # optimization algorithm, hyperotp will select its parameters automatically max_evals=50, # maximum number of iterations trials=trials, # logging rstate=np.random.RandomState(random_state) # fixing random state for the reproducibility )

computing the score on the test set

model = LGBMRegressor(random_state=random_state, n_estimators=int(best[‘n_estimators’]), max_depth=int(best[‘max_depth’]),learning_rate=best[‘learning_rate’]) model.fit(train_data,train_targets) tpe_test_score=mean_squared_error(test_targets, model.predict(test_data)) end=timeit.default_timer() info_end = psutil.Process(os.getpid()).memory_info().rss/1024/1024

print(‘此程序运行占内存’+str(info_end-info_start)+’mB’) print(‘Running time:%.5fs’%(end-start)) print(“Best MSE {:.3f} params {}”.format( gb_mse_cv(best), best)) ``` 实验结果：
此程序运行占内存2.5859375mB
Running time:52.73683s
Best MSE 3186.791 params {‘learning_rate’: 0.026975706032324936, ‘max_depth’: 20.0, ‘n_estimators’: 168.0}

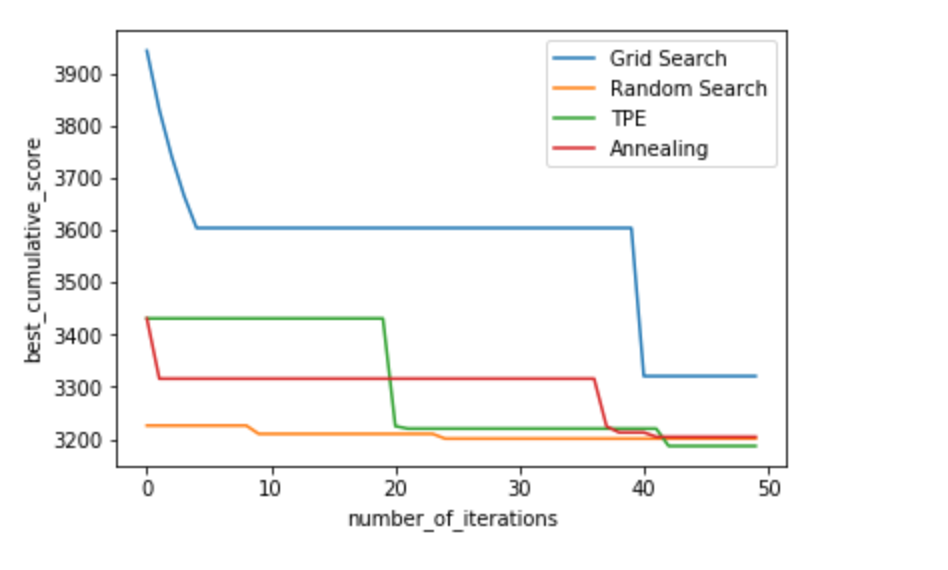
四、结论

我们可以看到，即使在以后的步骤中，TPE和退火算法实际上仍会随着时间的推移不断改善搜索结果，而随机搜索在开始时就随机地找到了一个很好的解决方案，然后仅稍微改善了结果。 TPE和RandomizedSearch结果之间的当前差异很小，但是在某些具有超参数范围更加多样化的现实应用中，hyperopt可以显着改善时间/得分
image.png