时间序列分析就是发现时间序列的变动规律并使用该规律来预测的统计技术。时间序列分析基于以下三个假设：

  1. 假设事物发展规律趋势会延续到未来。
  2. 预测所依据的数据没有不规则性。
  3. 不考虑事物发展之间的因果关系。

时间序列分析主要包括两方面内容：第一是序列分解；第二是序列预测。

代码及数据地址：
https://github.com/SeafyLiang/machine_learning_study/tree/master/time_series

一、时间序列分解

一个时间序列包含三种影响因素：

  1. 长期趋势：在一个相当长的时间内表现为一种近似直线的持续向上、向下或平稳的趋势。
  2. 季节变动：受季节变化影响所形成的一种长度和幅度固定的短期周期波动，“季节”指的是周期，可以是周、月、年等。
  3. 不规则变动：受偶然因素的影响所形成的不规则波动，如股票市场受利好或者利空信息的影响，使得股票价格产生的波动。

时间序列按照季节性来分类，分为季节性时间序列和非季节性时间序列。

1.1 非季节性时间序列分解

MA（Moving Average）

移动平均是一种简单平滑技术，它通过在时间序列上逐项推移取一定项数的均值，来表现指标的长期变化和发展趋势。

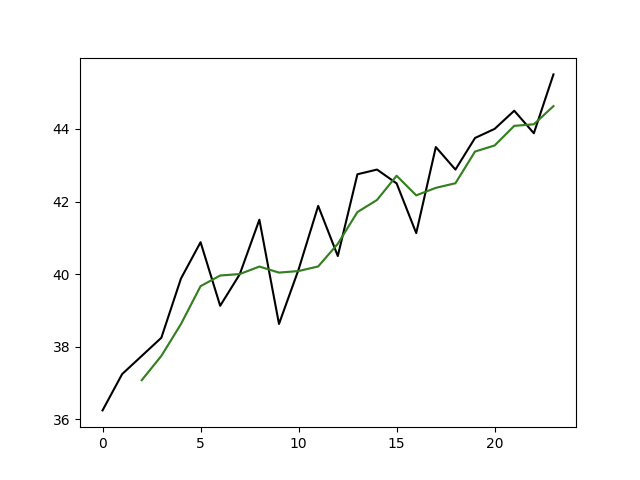
SMA（Simple Moving Average）

简单移动平均将时间序列上前n个数值做简单的算术平均。

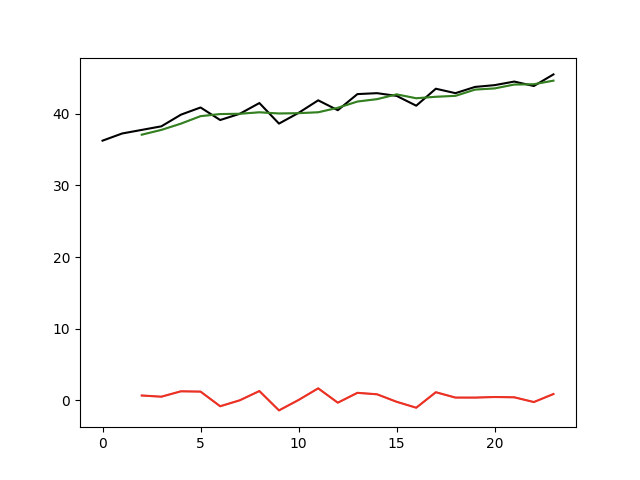
  1. import pandas as pd
  2. import numpy as np
  3. import matplotlib.pyplot as plt
  5. data = pd.read_csv('data/非季节性时间序列.csv', encoding='utf8', engine='python')
  7. original_data = data['公司A']
  10. def sma_demo():
  11.     # 将非季节性的时间序列，分解为趋势部分和不规则部分
  12.     # SMA 简单移动平均
  13.     sma_data = original_data.rolling(3).mean()
  14.     plt.plot(
  15.         data.index, original_data, 'k-',
  16.         data.index, sma_data, 'g-'
  17.     )
  18.     plt.show()
  19.     # 平滑后的曲线，波动性基本被消除
  21.     # 加入随机误差
  22.     random_error = original_data - sma_data
  23.     plt.plot(
  24.         data.index, original_data, 'k-',
  25.         data.index, sma_data, 'g-',
  26.         data.index, random_error, 'r-'
  27.     )
  28.     plt.show()
  29.     # 随机误差在0附件波动，均值趋向于0
  32. if __name__ == '__main__':
  33.     sma_demo()

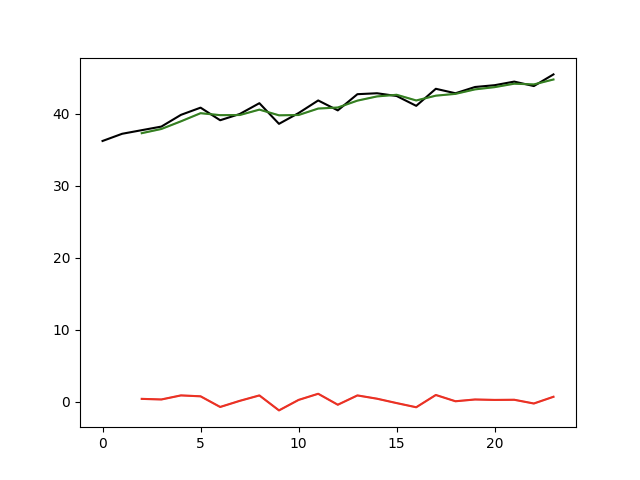
image.pngimage.png

WMA（Weighted Moving Average）

加权移动平均在基于简单移动平均的基础上，对时间序列上前n期的每一期数值赋予对应的权重。
它的基本思想是，提升近期的数据并减弱远期数据对当前预测值的影响，使平滑值更贴近最近的变化趋势。

  1. import pandas as pd
  2. import numpy as np
  3. import matplotlib.pyplot as plt
  5. data = pd.read_csv('data/非季节性时间序列.csv', encoding='utf8', engine='python')
  7. original_data = data['公司A']
  9. def wma_demo():
  10.     # WMA 加权移动平均
  11.     # 定义窗口大小
  12.     wl = 3
  13.     # 定义每个窗口值的权重
  14.     ww = [1 / 6, 2 / 6, 3 / 6]
  16.     def wma(window):
  17.         return np.sum(window * ww)
  19.     sma_data = original_data.rolling(wl).aggregate(wma)
  20.     random_error = original_data - sma_data
  21.     plt.plot(
  22.         data.index, original_data, 'k-',
  23.         data.index, sma_data, 'g-',
  24.         data.index, random_error, 'r-'
  25.     )
  26.     plt.show()
  29. if __name__ == '__main__':
  30.     wma_demo()

image.png

1.2 季节性时间序列

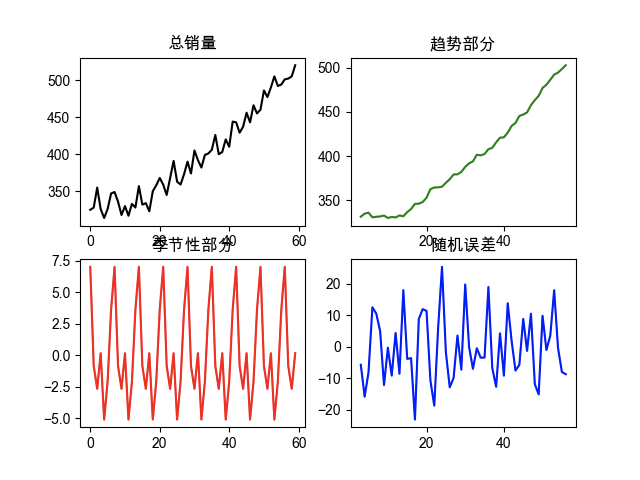
季节性时间序列，是指在一个时间序列中，若经过n个时间间隔后，呈现出相似的波动，则称该序列具有以n为周期的季节性特性。

  1. import pandas as pd
  2. import statsmodels.api
  3. import matplotlib.pyplot as plt
  4. plt.rcParams['font.sans-serif'] = ['Arial Unicode MS']
  7. data = pd.read_csv('data/季节性时间序列.csv', encoding='utf8', engine='python')
  9. total_sales = data['总销量'].values
  11. # 执行季节性时间序列分解
  12. '''
  13. statsmodels.api.tsa.seasonal_decompose(x, freq=None)
  14. x：要分解的季节性时间序列
  15. freq：时间序列的周期，需要自己根据业务来判断数据的周期
  16. '''
  17. tsr = statsmodels.api.tsa.seasonal_decompose(
  18.     total_sales, period=7
  19. )
  20. # 获取趋势部分
  21. trend = tsr.trend
  22. # 获取季节性部分
  23. seasonal = tsr.seasonal
  24. # 获取随机误差部分
  25. random_error = tsr.resid
  27. # 生成2*2的子图
  28. fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2, 2)
  30. ax1.set_title('总销量')
  31. ax1.plot(
  32.     data.index, total_sales, 'k-'
  33. )
  35. ax2.set_title('趋势部分')
  36. ax2.plot(
  37.     data.index, trend, 'g-'
  38. )
  40. ax3.set_title('季节性部分')
  41. ax3.plot(
  42.     data.index, seasonal, 'r-'
  43. )
  45. ax4.set_title('随机误差')
  46. ax4.plot(
  47.     data.index, random_error, 'b-'
  48. )
  49. plt.show()

image.png

二、序列预测

时间序列预测，是根据时间序列反映出来的发展过程、方向和趋势，进行类推或延伸，借以预测下一段时间或以后若干周期内可能达到的水平。

时间序列预测使用时间序列的均值、方差和协方差这三个统计量来刻画时间序列的本质特征。若这些统计量的值在过去和未来仍保持不变，则为平稳的时间序列。

2.1 不平稳时间序列转换成平稳的时间序列

如果时间序列不平稳，则需要通过差分等技术手段，把它转换成平稳的时间序列，然后再进行预测。

差分（Integrated）

在pandas模块中，使用diff函数，即可对数据进行差分。

单位根检验法

可以使用单位根检验法来检验一个时间序列的平稳性。其中的p-value代表有多大的概率不是一个平稳的时间序列。

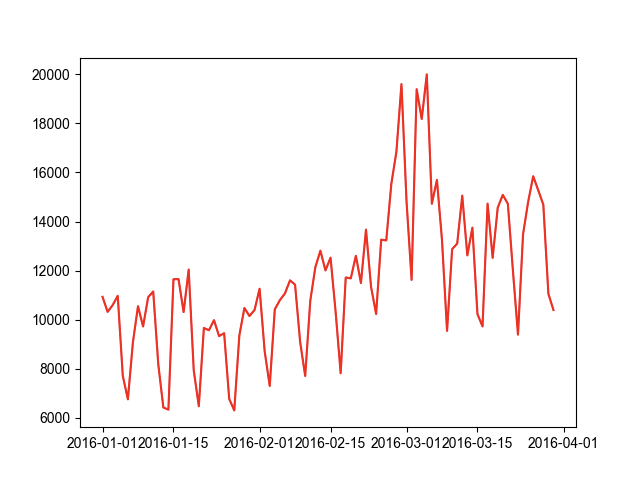
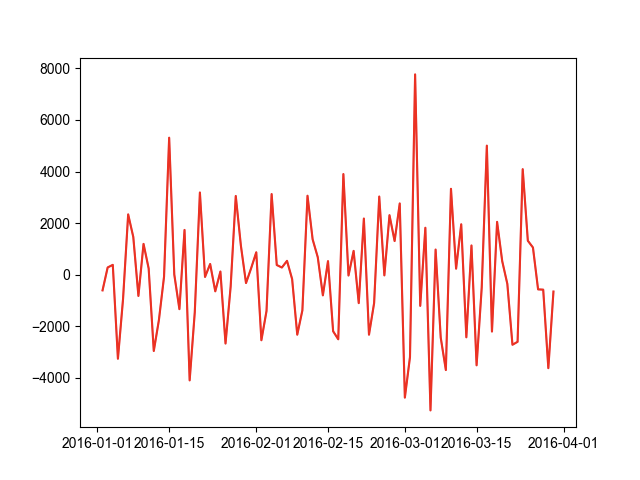
  1. import pandas as pd
  2. import matplotlib.pyplot as plt
  3. # 单位根检验法
  4. import statsmodels.tsa.stattools as ts
  6. plt.rcParams['font.sans-serif'] = ['Arial Unicode MS']
  7. '''
  8. 一个平稳的时间序列指的是，未来的时间序列，它的均值、方差和协方差必定与现在的时间序列相等。
  9. 若时间序列不平稳，则需要通过差分等技术手段，把它转换成平稳的时间序列，然后再进行预测。
  10. '''
  11. data = pd.read_csv('data/时间序列预测.csv', encoding='utf8', engine='python')
  13. # 设置索引为时间格式
  14. data.index = pd.to_datetime(data.date, format='%Y%m%d')
  15. # 删除date列，已经保存到索引中了
  16. del data['date']
  17. plt.figure()
  18. plt.plot(data, 'r')
  19. plt.show()
  22. # 使用单位根检验法检验是否是平稳的时间序列
  23. # 封装一个方法，方便解读adfuller函数的结果
  24. def tagADF(t):
  25.     result = pd.DataFrame(index=[
  26.         "Test Statistic Value",
  27.         "p-value", "Lags Used",
  28.         "Number of Observations Used",
  29.         "Critical Value(1%)",
  30.         "Critical Value(5%)",
  31.         "Critical Value(10%)"
  32.     ], columns=['value']
  33.     )
  34.     result['value']['Test Statistic Value'] = t[0]
  35.     result['value']['p-value'] = t[1]
  36.     result['value']['Lags Used'] = t[2]
  37.     result['value']['Number of Observations Used'] = t[3]
  38.     result['value']['Critical Value(1%)'] = t[4]['1%']
  39.     result['value']['Critical Value(5%)'] = t[4]['5%']
  40.     result['value']['Critical Value(10%)'] = t[4]['10%']
  41.     return result
  44. # 使用ADF单位根检验法，检验时间序列的稳定性
  45. adf_data = ts.adfuller(data.value)
  47. # 解读ADF单位根检验结果
  48. adfResult = tagADF(adf_data)
  49. print(adfResult)
  50. #                                 value
  51. # Test Statistic Value         -1.16364
  52. # p-value                      0.689038
  53. # Lags Used                          12
  54. # Number of Observations Used        77
  55. # Critical Value(1%)          -3.518281
  56. # Critical Value(5%)          -2.899878
  57. # Critical Value(10%)         -2.587223
  59. # 68%的概率不是一个平稳的时间序列，故通过差分转换成平稳的时间序列
  60. # 对数据进行差分，删除第一个位置的空值
  61. diff = data.value.diff(1).dropna()
  63. plt.figure()
  64. plt.plot(diff, 'r')
  65. plt.show()
  67. # 使用ADF单位根检验法，检验时间序列的稳定性
  68. adf_diff = ts.adfuller(diff)
  70. # 解读ADF单位根检验结果
  71. adfResult = tagADF(adf_diff)
  72. print(adfResult)
  73. #                                 value
  74. # Test Statistic Value        -4.993859
  75. # p-value                      0.000023
  76. # Lags Used                          12
  77. # Number of Observations Used        76
  78. # Critical Value(1%)          -3.519481
  79. # Critical Value(5%)          -2.900395
  80. # Critical Value(10%)         -2.587498
  82. # 0.000023<0.05，认为差分后的时间序列是平稳的时间序列

image.pngimage.png

2.2 自回归模型-AR

自回归模型本质是一个线性回归模型，“自”描述的是当前值与历史值之间的关系。通过一个超参数p，把时间序列格式的样本转换为线性回归模型的样本。

2.3 移动平均模型-MA

移动平均模型描述的是自回归模型部分的累计误差。
移动平均模型的意义在于，找到较少参数的移动平均模型，来替代较多参数的自回归模型。

2.4 自回归移动平均模型-ARMA

ARMA模型就是AR模型和MA模型的组合，将因变量仅对它的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型。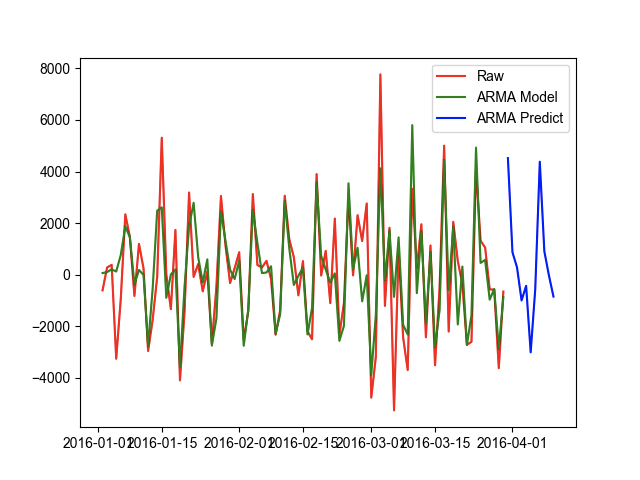
image.pngimage.png

2.5 时序预测代码-AR, MA, ARMA

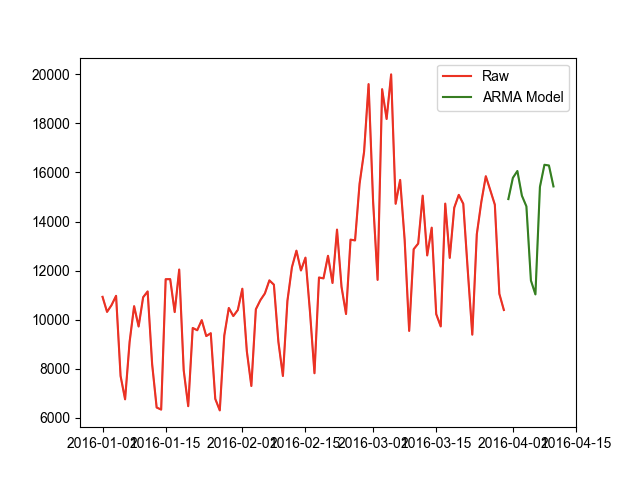
  1. import statsmodels.api as sm
  2. import pandas as pd
  3. import matplotlib.pyplot as plt
  4. import warnings
  6. warnings.filterwarnings("ignore")
  7. plt.rcParams['font.sans-serif'] = ['Arial Unicode MS']
  9. data = pd.read_csv('data/时间序列预测.csv', encoding='utf8', engine='python')
  11. # 设置索引为时间格式
  12. data.index = pd.to_datetime(data.date, format='%Y%m%d')
  13. # 删除date列，已经保存到索引中了
  14. del data['date']
  16. diff = data.value.diff(1).dropna()
  18. plt.figure()
  19. plt.plot(diff, 'r')
  20. plt.show()
  23. def ar_demo():
  24.     '''
  25.     自回归
  26.     :return:
  27.     '''
  28.     # 使用 AR 建模
  29.     arModel = sm.tsa.AR(
  30.         diff
  31.     )
  33.     # 使用 AR 模型的 select_order 方法
  34.     # 自动根据 AIC 指标，选择最优的 p 值
  35.     p = arModel.select_order(
  36.         maxlag=30,
  37.         ic='aic'
  38.     )
  39.     print(p)
  41.     # 使用最优的 p 值进行建模
  42.     arModel = arModel.fit(maxlag=p)
  44.     # 对时间序列模型进行评估
  45.     delta = arModel.fittedvalues - diff
  46.     score = 1 - delta.var() / diff.var()
  47.     print(score)
  50. def sma_demo():
  51.     '''
  52.     简单移动平均
  53.     :return:
  54.     '''
  55.     sma_data = diff.rolling(3).mean()
  56.     plt.plot(
  57.         diff.index, diff, 'k-',
  58.         diff.index, sma_data, 'g-'
  59.     )
  60.     plt.show()
  63. def arma_demo():
  64.     # ARMA模型，使用AIC指标
  65.     # AR模型从1-15中选择最优的p
  66.     # MA模型从1-15中选择最优的q
  67.     # 执行时间非常长，作者执行了10个小时左右
  68.     # ic = sm.tsa.arma_order_select_ic(
  69.     #     diff,
  70.     #     max_ar=15,
  71.     #     max_ma=15,
  72.     #     ic='aic'
  73.     # )
  74.     # 选择最优参数
  75.     order = (6, 6)
  77.     armaModel = sm.tsa.ARMA(
  78.         diff, order
  79.     ).fit()
  80.     # 评估模型得分
  81.     delta = armaModel.fittedvalues - diff
  82.     score = 1 - delta.var() / diff.var()
  83.     print(score)
  85.     # 预测接下来10天的值
  86.     p = armaModel.predict(
  87.         start='2016-03-31',
  88.         end='2016-04-10'
  89.     )
  91.     # 封装一个对差分的数据进行还原的函数
  92.     def revert(diffValues, *lastValue):
  93.         for i in range(len(lastValue)):
  94.             result = []
  95.             lv = lastValue[i]
  96.             for dv in diffValues:
  97.                 lv = dv + lv
  98.                 result.append(lv)
  99.             diffValues = result
  100.         return diffValues
  102.     # 对差分的数据进行还原
  103.     r = revert(p, 10395)
  105.     plt.figure()
  106.     plt.plot(
  107.         diff, 'r',
  108.         label='Raw'
  109.     )
  110.     plt.plot(
  111.         armaModel.fittedvalues, 'g',
  112.         label='ARMA Model'
  113.     )
  114.     plt.plot(
  115.         p, 'b', label='ARMA Predict'
  116.     )
  117.     plt.legend()
  118.     plt.show()
  120.     r = pd.DataFrame({
  121.         'value': r
  122.     }, index=p.index
  123.     )
  124.     plt.figure()
  125.     plt.plot(
  126.         data.value, c='r',
  127.         label='Raw'
  128.     )
  129.     plt.plot(
  130.         r, c='g',
  131.         label='ARMA Model'
  132.     )
  133.     plt.legend()
  134.     plt.show()
  137. if __name__ == '__main__':
  138.     ar_demo()
  139.     sma_demo()
  140.     arma_demo()