06基于标准差和箱体图的单指标异常点检测

在数据的处理过程中，不可避免的会产生缺失值、异常值，下面来讲一下我在工作中使用到的两种常见的判断异常值的方法。

一、基于箱体图

箱体图，即箱线图，从下到上五条线分别表示最小值、下四分位数、中位数、上四分位数和最大值。
百度百科-箱线图
箱体图是一种用于显示一组数据分散情况资料的统计图，可以通过设定标准，将大于或小于箱体图上下界的数值识别为异常值。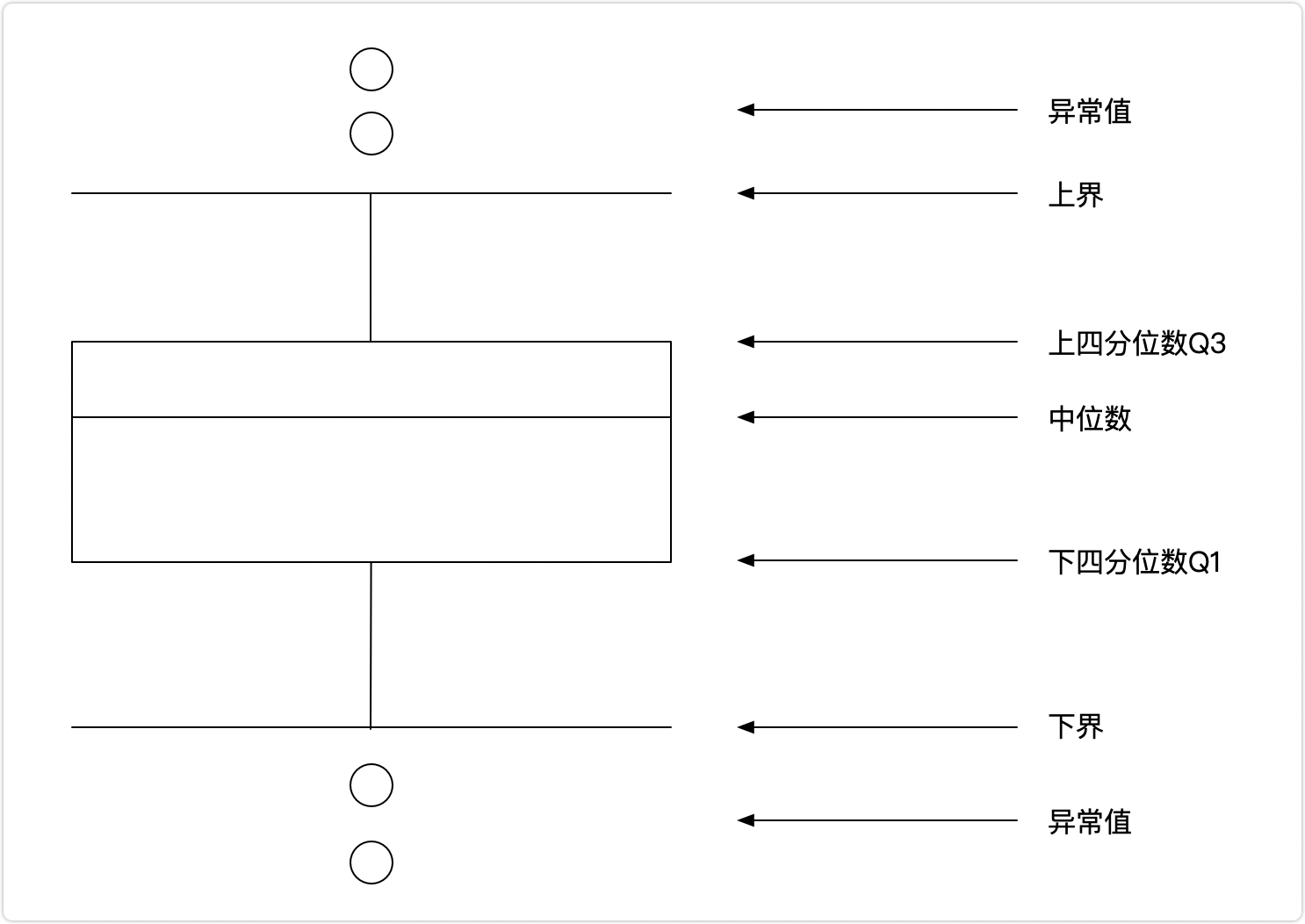

如上图所示，
将数据的下四分位数记为Q1，即样本中仅有25%的数据小于Q1；
将数据的上四分位数记为Q3，即样本中仅有25%的数据大于Q3；
将上四分位数和下四分位数的差值记为IQR，即IQR=Q3-Q1；
令箱体图上界为Q3+1.5*IQR，下界为Q1-1.5*IQR。

import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_csv('data/od_test.csv')
df.boxplot()
plt.show()

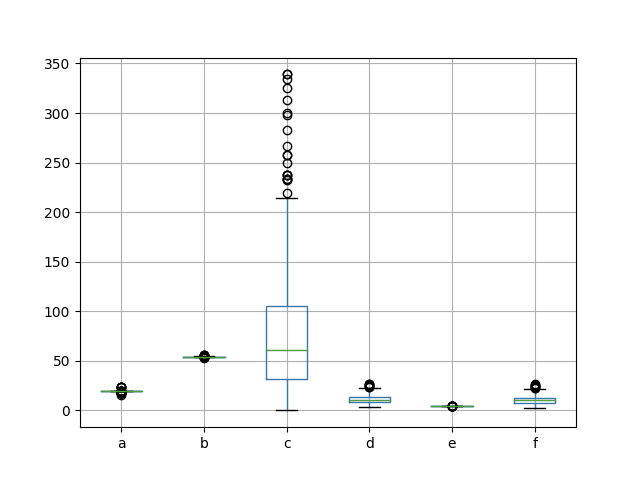
如上图所示，c列有很多的异常值。

二、基于标准差

当数据服从标准正态分布时，99%的数值与均值的距离应该在3个标准差之内，95%的数值与均值的距离应该在2个标准差之内，如下图所示。
当数值与均值的距离超出3个标准差，则可认为它是异常值。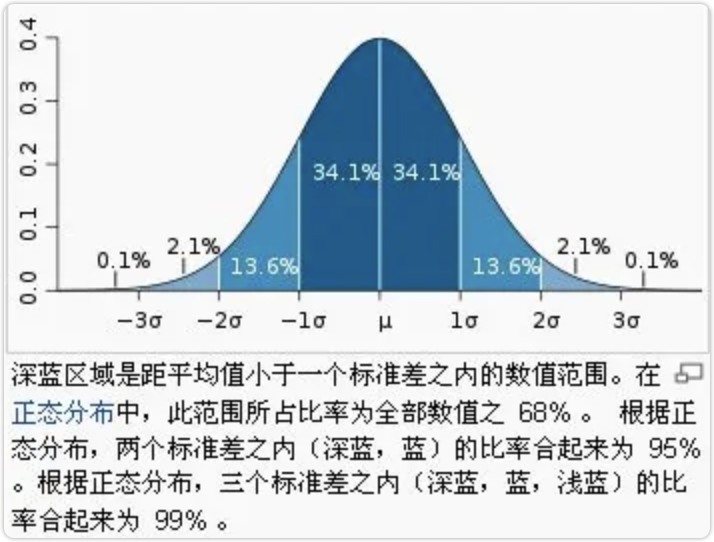

百度百科-标准差

s = df_notnull[od_column]
# 标准差上下限计算
normal_mean = s.mean()
normal_std = s.std()
std_lower = normal_mean - 3 * normal_std
std_upper = normal_mean + 3 * normal_std

三、效果图及数据代码获取方式

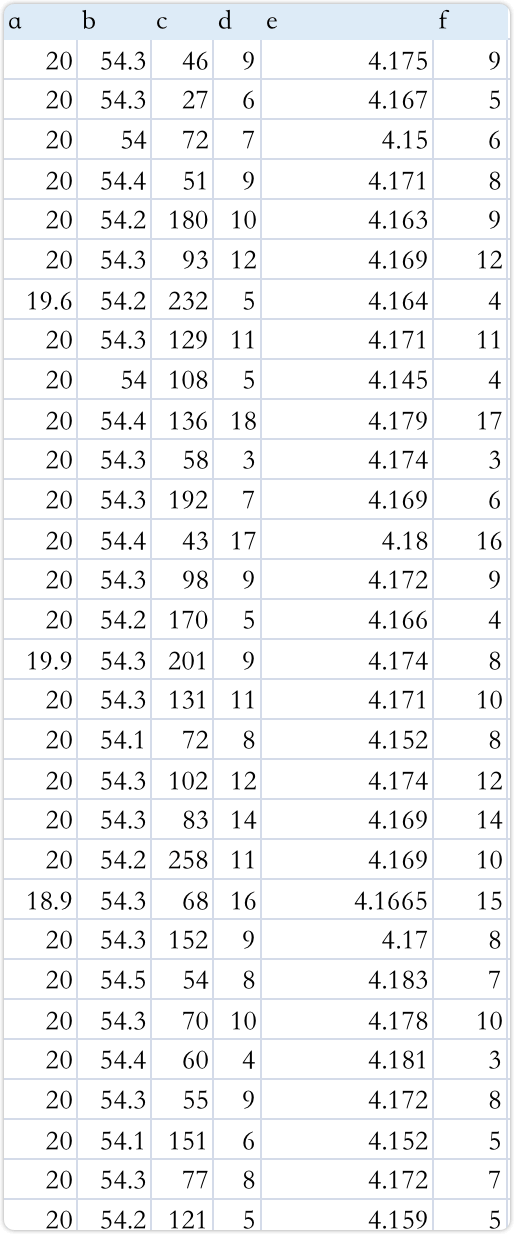
3.1 原数据

3.2 检测结果汇总表格：

检测结果包含：
[指标名，总数据量，非空数据量，空值数据量，无效值数据量，零值数据量，正常平均值，正常标准差，标准差上界，标准差下界，箱体图上界，箱体图下界，箱体图检测异常数据量，标准差检测异常数据量等等…]

3.3 数据及代码获取：

github：https://github.com/SeafyLiang/Python_study/blob/master/pandas_study/single_od.py
国内：https://gitee.com/seafyLiang/Python_study/blob/master/pandas_study/single_od.py