参考资料：https://mp.weixin.qq.com/s/o7Xkdh7ew-6KGsIi80iayg

HBOS全名为：Histogram-based Outlier Score。它是一种单变量方法的组合，不能对特征之间的依赖关系进行建模，但是计算速度较快，对大数据集友好，其基本假设是数据集的每个维度相互独立，然后对每个维度进行区间(bin)划分，区间的密度越高，异常评分越低。理解了这句话，基本就理解了这个算法。下面我专门画了两个图来解释这句话。

一、HBOS算法流程

1、静态宽度直方图

标准的直方图构建方法，在值范围内使用k个等宽箱，样本落入每个箱的频率（相对数量）作为密度（箱子高度）的估计，时间复杂度：O(n)
注意：等宽分箱，每个箱中的数据宽度相同，不是指数据个数相同。例如序列[5,10,11,13,15,35,50,55,72,92,204,215]，数据集中最大值是215，最小值是5，分成3个箱，故每个箱的宽度应该为（215-5）/3=70，所以箱的宽度是70，这就要求箱中数据之差不能超过70，并且要把不超过70的数据全放在一起，最后的分箱结果如下：
箱一：5,10，11,13,15,35,50,55,72；箱二：92；箱三：204,215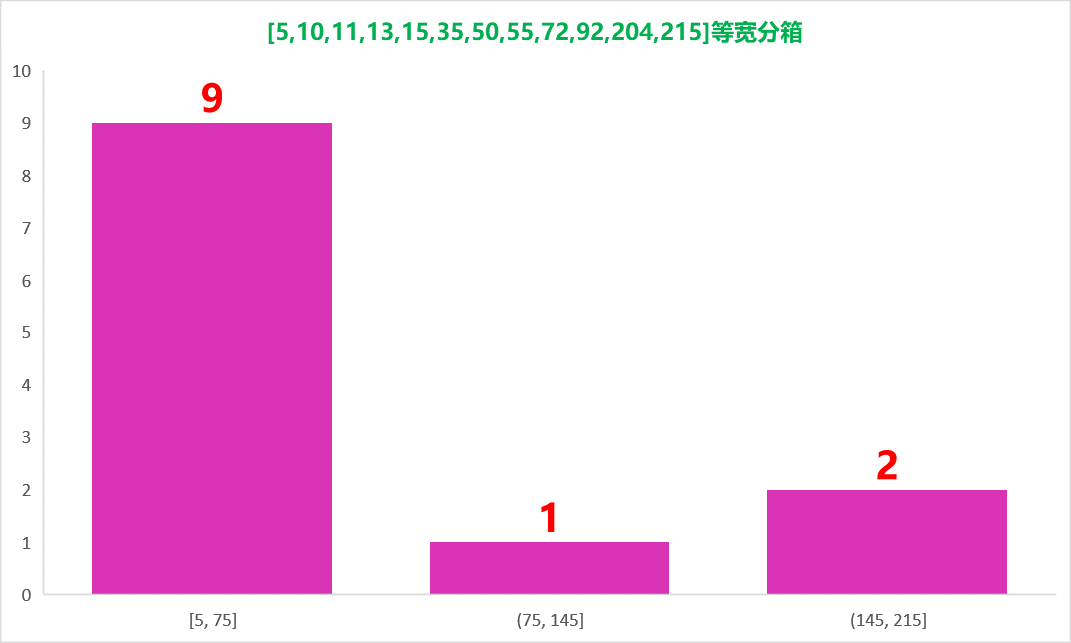
HBOS异常点检测 - 图1

这个是分5箱的图
HBOS异常点检测 - 图2

2、动态宽度直方图

首先对所有值进行排序，然后固定数量的N/k 个连续值装进一个箱里，其中N是总实例数，k是箱个数，直方图中的箱面积表示实例数，因为箱的宽度是由箱中第一个值和最后一个值决定的，所有箱的面积都一样，因此每一个箱的高度都是可计算的。这意味着跨度大的箱的高度低，即密度小，只有一种情况例外，超过k个数相等，此时允许在同一个箱里超过N/k值，时间复杂度：O(n×log(n))
还是用序列[5,10,11,13,15,35,50,55,72,92,204,215]举例，也是假如分3箱，那么每箱都是4个，宽度为边缘之差，第一个差为15-5=10，第二差为72-35=37，第三个箱宽为215-92=123，为了保持面积相等，所以导致后面的很矮，前面的比较高，如下图所示（非严格按照规则）：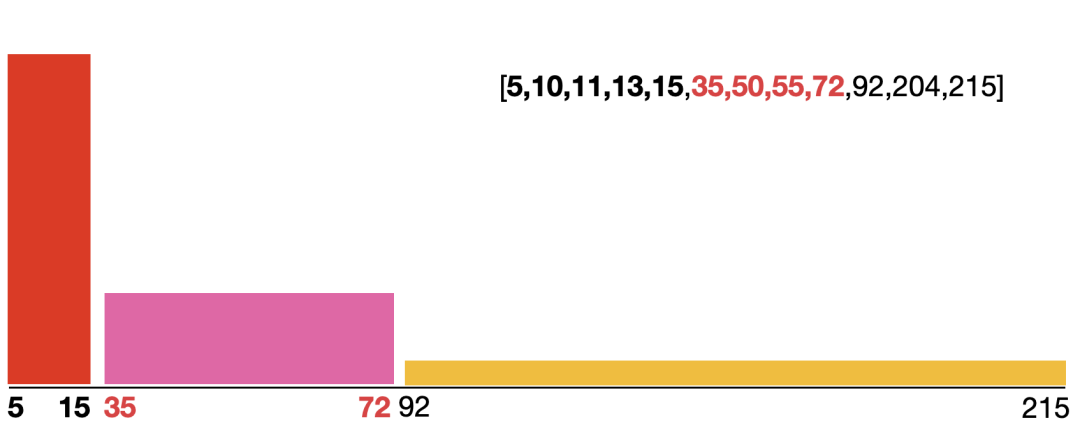
HBOS异常点检测 - 图3

二、算法推导过程

对每个维度都计算了一个独立的直方图，其中每个箱子的高度表示密度的估计，然后为了使得最大高度为1（确保了每个特征与异常值得分的权重相等），对直方图进行归一化处理。最后，每一个实例的HBOS值由以下公式计算：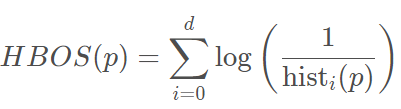
HBOS异常点检测 - 图4
推导过程：
假设样本p第 i 个特征的概率密度为p i ( p ) ，则p的概率密度可以计算为，d为总的特征的个数：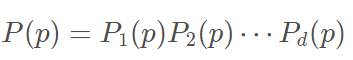
HBOS异常点检测 - 图5
两边取对数：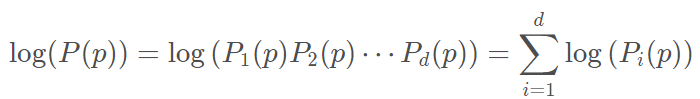
HBOS异常点检测 - 图6
概率密度越大，异常评分越小，为了方便评分，两边乘以“-1”：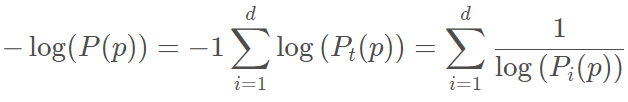
HBOS异常点检测 - 图7
最后可得：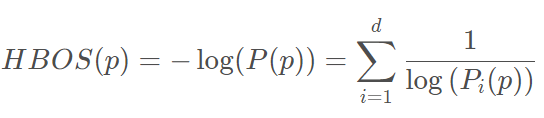
HBOS异常点检测 - 图8
PyOD是一个可扩展的Python工具包，用于检测多变量数据中的异常值。它可以在一个详细记录API下访问大约20个离群值检测算法。

三、应用案例详解

1、基本用法

from pyod.models.hbos 
HBOSHBOS(
    n_bins=10, 
    alpha=0.1, 
    tol=0.5, 
    contamination=0.1
       )

2、模型参数

n_bins：分箱的数量
alpha：用于防止边缘溢出的正则项
tol：用于设置当数据点落在箱子外时的宽容度
contamination：用于设置异常点的比例

3、应用案例

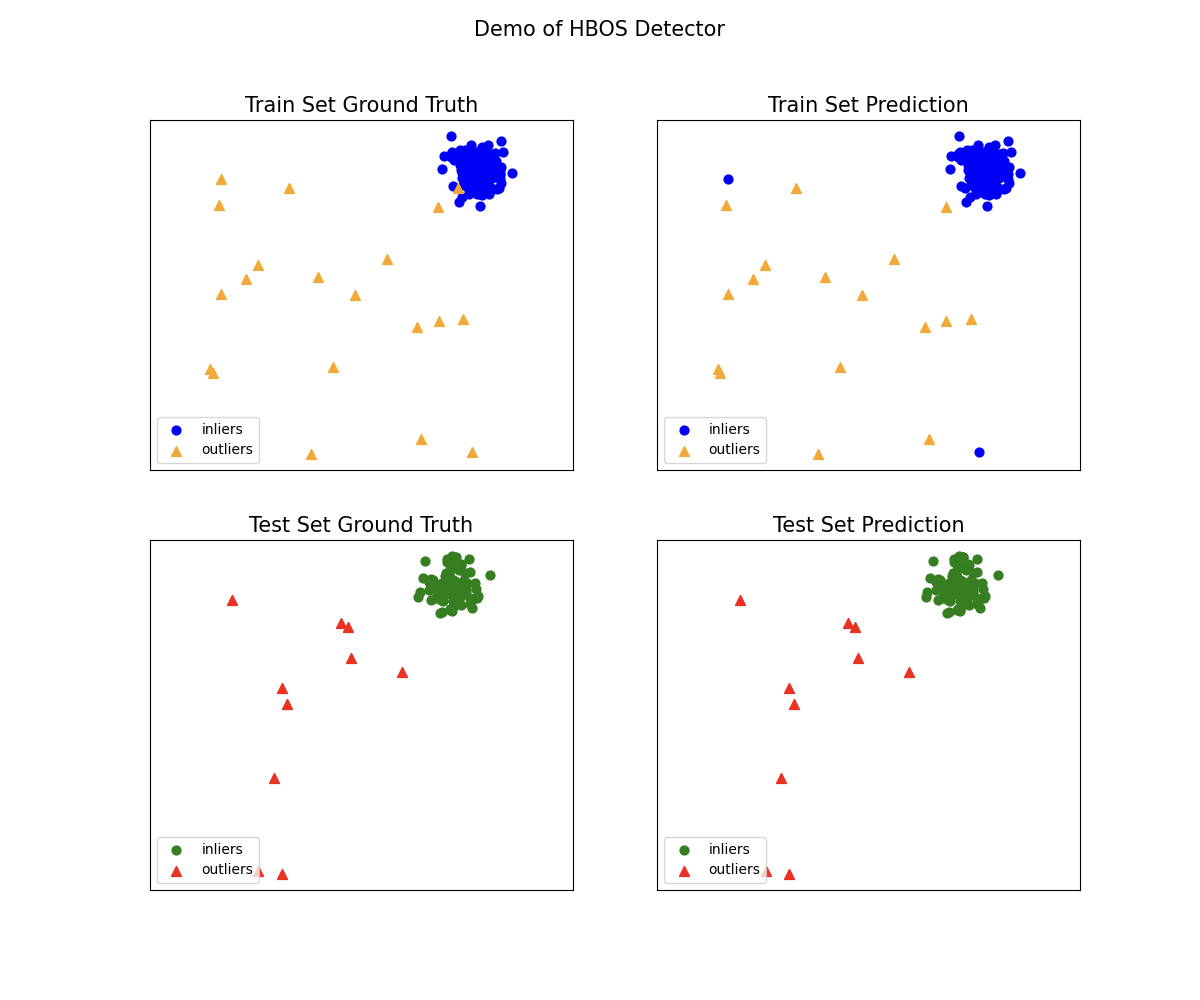
# 导入包
from pyod.utils.data import generate_data, evaluate_print
# 样本的生成
X_train, y_train, X_test, y_test = generate_data(n_train=200, n_test=100, contamination=0.1)
print(X_train.shape)
# (200, 2)
print(X_test.shape)
# (100, 2)
from pyod.models import hbos
from pyod.utils.example import visualize
# 模型训练
clf = hbos.HBOS()
clf.fit(X_train)
y_train_pred = clf.labels_
y_train_socres = clf.decision_scores_
# 返回未知数据上的分类标签 (0: 正常值, 1: 异常值)
y_test_pred = clf.predict(X_test)
# 返回未知数据上的异常值 (分值越大越异常)
y_test_scores = clf.decision_function(X_test)
print(y_test_pred)
# [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
#  0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
#  0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1]
print(y_test_scores)
# [-0.90209111 -0.90209111 -0.09322378 -0.44865128 -0.09322378 -0.44865128
#  -0.90209111 -0.09322378  0.36021604 -0.44865128 -0.90209111 -0.09322378
#  -0.90209111  2.00232582 -0.44865128 -0.09322378 -0.44865128 -0.90209111
#  -0.90209111 -0.90209111 -0.90209111 -0.90209111 -0.09322378 -0.09322378
#  -0.09322378 -0.90209111 -0.90209111 -0.09322378 -0.90209111 -0.90209111
#  -0.09322378 -0.90209111 -0.09322378 -0.90209111 -0.44865128 -0.09322378
#  -0.44865128 -0.90209111 -0.90209111 -0.90209111 -0.44865128 -0.09322378
#   0.36021604 -0.09322378 -0.90209111 -0.90209111 -0.44865128 -0.90209111
#  -0.90209111 -0.09322378  2.00232582 -0.09322378 -0.44865128  0.36021604
#  -0.44865128 -0.44865128 -0.90209111 -0.44865128 -0.90209111 -0.90209111
#  -0.44865128 -0.44865128 -0.90209111 -0.90209111  0.36021604 -0.44865128
#  -0.09322378 -0.44865128 -0.90209111 -0.44865128 -0.90209111 -0.09322378
#   0.36021604 -0.90209111  0.36021604 -0.44865128 -0.90209111 -0.90209111
#  -0.44865128 -0.09322378 -0.90209111  0.36021604 -0.90209111 -0.09322378
#   0.36021604 -0.44865128 -0.90209111 -0.90209111 -0.09322378 -0.44865128
#   5.5335093   5.94991172  6.33881212  2.79916998  6.33881212  6.18587879
#   5.94991172  6.33035346  5.69806266  6.18587879]
# 模型评估
clf_name = 'HBOS'
evaluate_print(clf_name, y_test, y_test_scores)
# HBOS ROC:1.0, precision @ rank n:1.0
# 模型可视化
visualize(clf_name,
          X_train, y_train,
          X_test, y_test,
          y_train_pred, y_test_pred,
          show_figure=True,
          save_figure=False
          )

四、总结

HBOS这个算法原理简单，复杂度低，在大数据场景比较好用，但是异常识别的效果一般，且针对特征间比较独立的场景，简单点讲该算法就是把数据划分为多个区间，然后根据每个区间的频次根据概率密度函数转化为对应的出现概率，在将这个概率转化为异常分数，以此来区分异常数据
因此HBOS在全局异常检测问题上表现良好，但在局部异常的检测上效果一般。

HBOS异常点检测