参考资料:公众号:机器学习研习院-九种顶流回归算法及实例总结
- 线性回归
- LinearRegression
- 多项式回归
- PolynomialFeatures
- 支持向量回归
- SVR
- 决策树回归
- DecisionTreeRegressor
- 随机森林回归
- RandomForestRegressor
- LASSO回归
- LassoCV
- 岭回归
- RidgeCV
- ElasticNet回归
- ElasticNetCV
- XGBoost回归
- XGBRegressor
线性回归通常是人们为机器学习和数据科学学习的第一个算法。它简单易懂,但是由于其功能有限,在实际业务中并不是最佳选择。大多数情况下,线性回归被用作基线模型来评估和比较研究中的新方法。
在处理实际问题时,我们应该了解并尝试过许多其他回归算法。在本文中,将通过使用Scikit-learn和 XGBoost 的动手练习来学习 9 种流行的回归算法。本文的结构如下: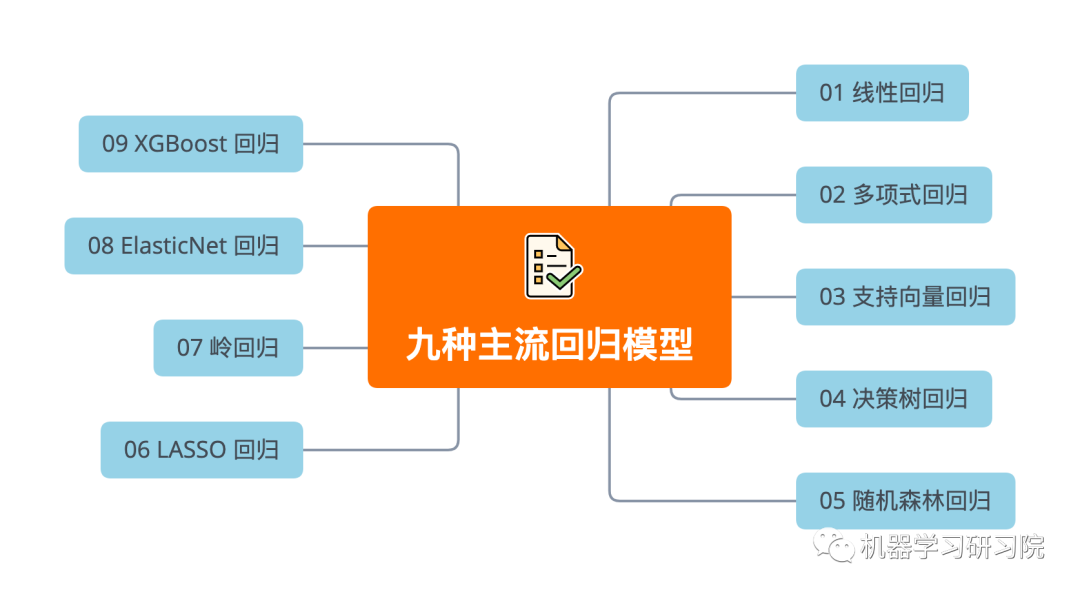
写在前面
本次数据使用的是一个藏在Python第三方vegadatasets模块中的著名的数据科学公开数据集。
vega_datasets里的数据集内容挺多,有统计数据也有地理数据,还有不同数据量的版本,例如flights数据集包含了2k、5k、200k、3m等多个版本。调用是写:df = data(‘iris’)或者df = data.iris(),数据存在在_Anaconda3/Lib/site-packages/vega_datasets目录下,存本地的在local_datasets.json里有描述。本地存的有csv格式的也有json格式的。
pip3 install vega_datasets
导入和使用数据集
from vega_datasets import dataimport pandas as pddf = data.cars()df.head()
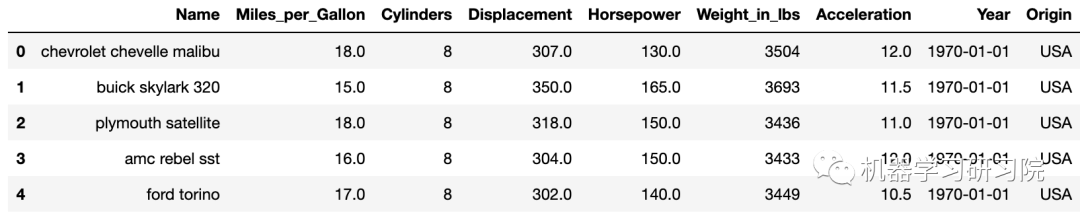
df.info()
RangeIndex: 406 entries, 0 to 405
Data columns (total 9 columns):
# Column Non-Null Count Dtype
—- ——— ——————— ——-
0 Name 406 non-null object
1 Miles_per_Gallon 398 non-null float64
2 Cylinders 406 non-null int64
3 Displacement 406 non-null float64
4 Horsepower 400 non-null float64
5 Weight_in_lbs 406 non-null int64
6 Acceleration 406 non-null float64
7 Year 406 non-null datetime64[ns]
8 Origin 406 non-null object
dtypes: datetime64ns, float64(4), int64(2), object(2)
memory usage: 28.7+ KB
数据处理
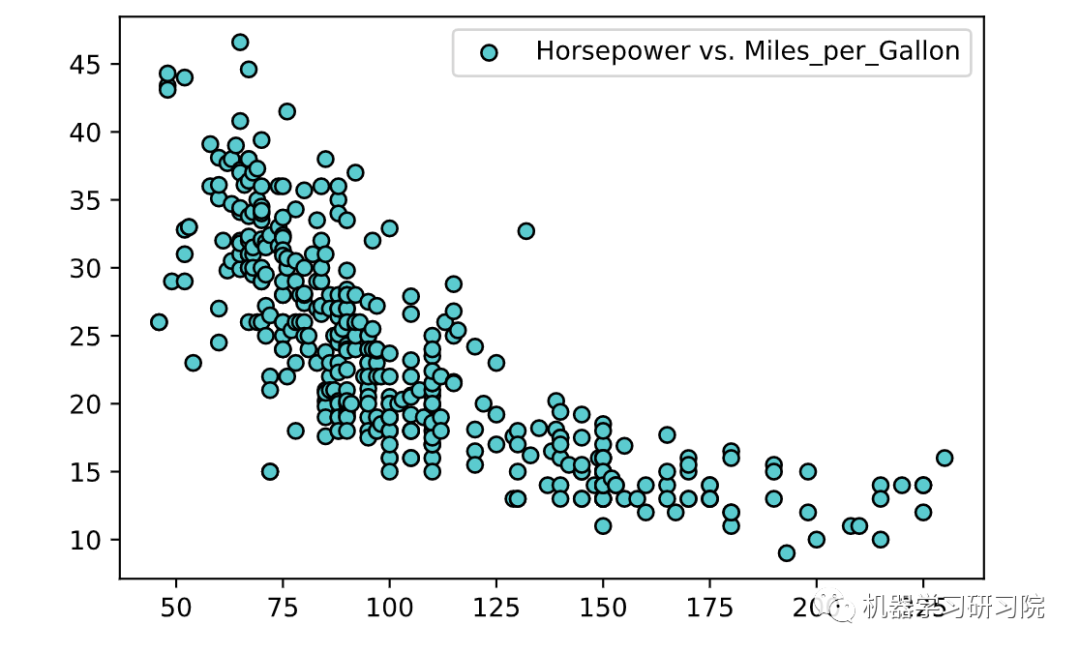
# 过滤特定列中的NaN行df.dropna(subset=['Horsepower', 'Miles_per_Gallon'], inplace=True)df.sort_values(by='Horsepower', inplace=True)# 数据转换X = df['Horsepower'].to_numpy().reshape(-1, 1)y = df['Miles_per_Gallon'].to_numpy().reshape(-1, 1)plt.scatter(X, y, color='teal', edgecolors='black', label='Horsepower vs. Miles_per_Gallon')plt.legend()plt.show()
01 线性回归
线性回归通常学习机器学习与数据科学的第一个算法。线性回归是一种线性模型,它假设输入变量 ( X) 和单个输出变量 ( y)之间存在线性关系。一般来说,有两种情况:
- 单变量线性回归:它表示单个输入变量和单个的输出变量模型之间的关系。
- 多变量线性回归(也称为多元线性回归):它对多个输入变量和单个输出变量之间的关系进行建模。
这个算法很常见,Scikit-learn[2]内置简单线性回归LinearRegression()算法。接下来就和小猴子一起创建一个LinearRegression对象,并使用训练数据进行训练。
from sklearn.linear_model import LinearRegression # 创建和训练模型linear_regressor = LinearRegression()linear_regressor.fit(X, y)
训练完成后,可以使用LinearRegression的coef_属性中查看模型系数参数:
linear_regressor.coef_
array([[-0.15784473]])
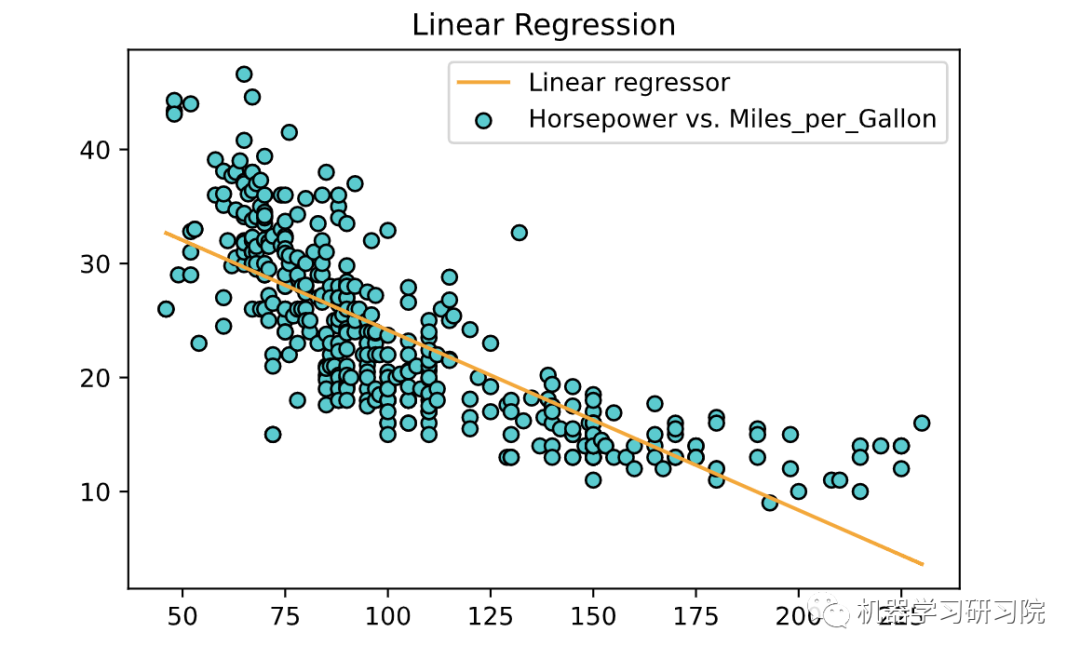
现在使用训练好的模型并为训练数据拟合一条线
# 为训练数据绘制点和拟合线plt.scatter(X, y, color='RoyalBlue', edgecolors='black', label='Horsepower vs. Miles_per_Gallon')plt.plot(X, linear_regressor.predict(X), color='orange', label='Linear regressor')plt.title('Linear Regression')plt.legend()plt.show()
小结
关于线性回归的几个关键点:
- 快速且易于建模
- 当要建模的关系不是非常复杂并且没有大量数据时,线性回归特别有用。
- 非常直观的理解和解释。
-
02 多项式回归
当想要为非线性可分数据创建模型时,多项式回归是最受欢迎的选择之一。它类似于线性回归,但使用变量X和y之间的关系并为数据点找到绘制适合曲线的最佳方法。
对于多项式回归,一些自变量的幂大于 1。例如,可能提出如下的二次模型: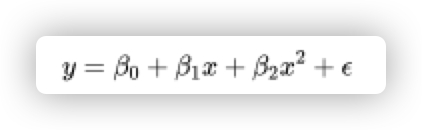
β_0, β_1, 和β_2是系数
- x 是一个变量/特征
- ε 是残差
Scikit-learn内置多项式回归PolynomialFeatures。首先,我们需要生成一个由所有具有指定次数的多项式特征组成的特征矩阵:
from sklearn.preprocessing import PolynomialFeatures# 为二次模型生成矩阵# 这里只是简单地生成X^0 X^1和X^2的矩阵poly_reg = PolynomialFeatures(degree = 2 )X_poly = poly_reg.fit_transform(X)
接下来,让我们创建一个LinearRegression对象并将其拟合到X_poly我们刚刚生成的特征矩阵中。
# 多项式回归模型poly_reg_model = LinearRegression()poly_reg_model.fit(X_poly, y)
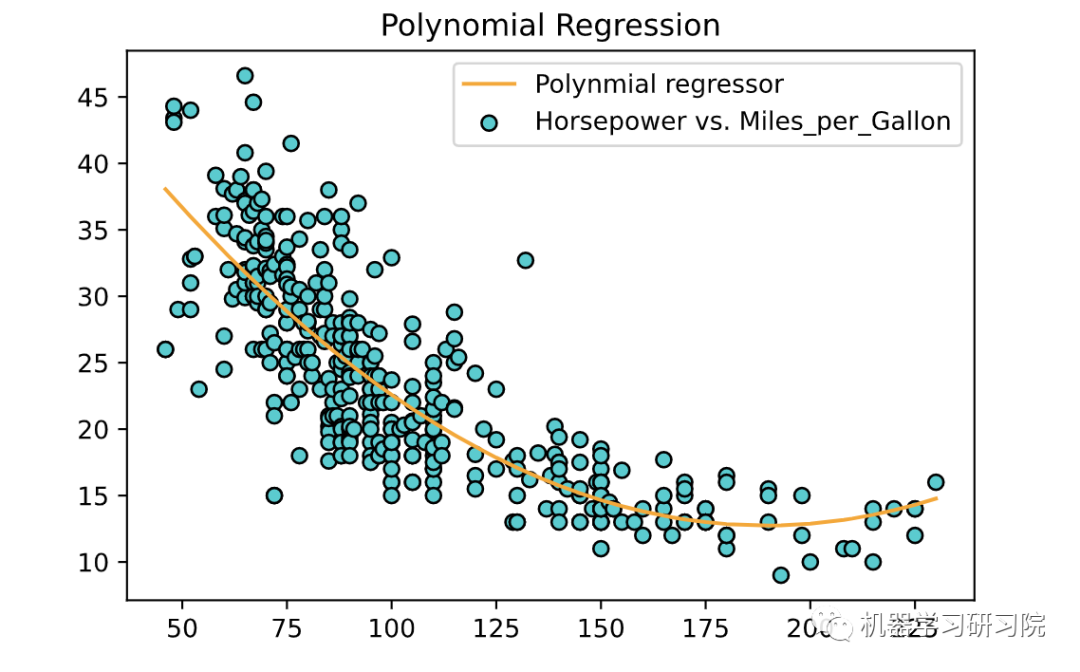
现在采用该模型并为训练数据拟合一条线,X_plot如下所示:
# 为训练数据绘制点和拟合线plt.scatter(X, y, color='DarkTurquoise', edgecolors='black',label='Horsepower vs. Miles_per_Gallon')plt.plot(X, poly_reg_model.predict(X_poly), color='orange',label='Polynmial regressor')plt.title('Polynomial Regression')plt.legend()plt.show()
小结
关于多项式回归的几个关键点:
- 能够对非线性可分数据进行建模;而线性回归不能做到这一点。它总体上更加灵活,可以对一些相当复杂的关系进行建模。
- 完全控制特征变量的建模(可指定设置指数)。
- 需要精心设计,需要一些数据知识才能选择最佳指数。
- 如果指数选择不当,则容易过度拟合。
03 支持向量回归
众所周知的支持向量机在处理分类问题时非常有效。其实,SVM 也经常用在回归问题中,被称为支持向量回归(SVR)。同样,Scikit-learn内置了这种方法SVR()。
在拟合 SVR 模型之前,通常较好的做法是对数据进行数据标准化操作,及对特征进行缩放。数据标准化的目的是为了确保每个特征都具有相似的重要性。我们通过StandardScaler()方法对训练数据操作。 ```python from sklearn.svm import SVR from sklearn.preprocessing import StandardScaler # 执行特征缩放 scaled_X = StandardScaler() scaled_y = StandardScaler()
scaled_X = scaled_X.fit_transform(X) scaled_y = scaled_y.fit_transform(y)
接下来,我们创建了一个SVR与对象**的内核**设置为'rbf'和**伽玛**设置为'auto'。之后,我们调用fit()使其适合缩放的训练数据:```pythonsvr_regressor = SVR(kernel='rbf', gamma='auto')svr_regressor.fit(scaled_X, scaled_y.ravel())
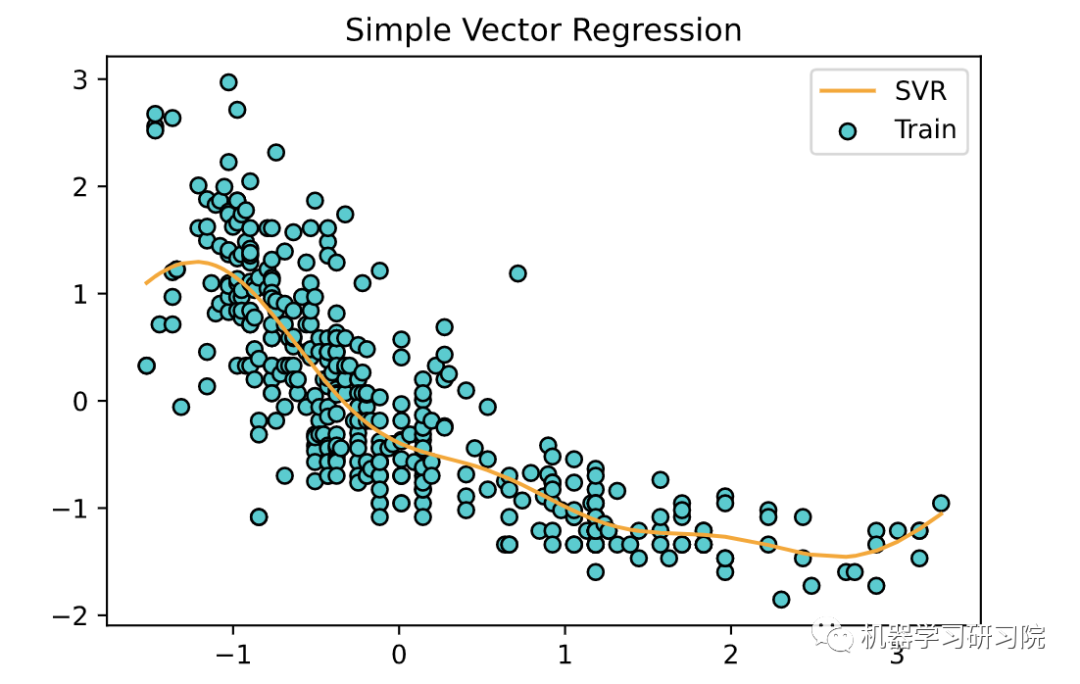
现在采用该模型并为训练数据拟合一条线,scaled_X如下所示:
plt.scatter(scaled_X, scaled_y, color='DarkTurquoise',edgecolors='black', label='Train')plt.plot(scaled_X, svr_regressor.predict(scaled_X),color='orange', label='SVR')plt.title('Simple Vector Regression')plt.legend()plt.show()
小结
支持向量回归的几个关键点
- 它对异常值具有鲁棒性并且在高维空间中有效
- 它具有出色的泛化能力(能够正确适应新的、以前看不见的数据)
- 如果特征数量远大于样本数量,则容易过拟合
04 决策树回归
决策树 (DT) 是一种用于分类和回归的非参数监督学习方法 。目标是创建一个树模型,通过学习从数据特征推断出的简单决策规则来预测目标变量的值。一棵树可以看作是分段常数近似。
决策树回归也很常见,以至于Scikit-learn内置了DecisionTreeRegressor. 甲DecisionTreeRegressor对象可以在没有特征缩放如下创建: ```python from sklearn.tree import DecisionTreeRegressor
不需要进行特性缩放,因为它将自己处理。
tree_regressor = DecisionTreeRegressor(random_state = 0) tree_regressor.fit(X, y)
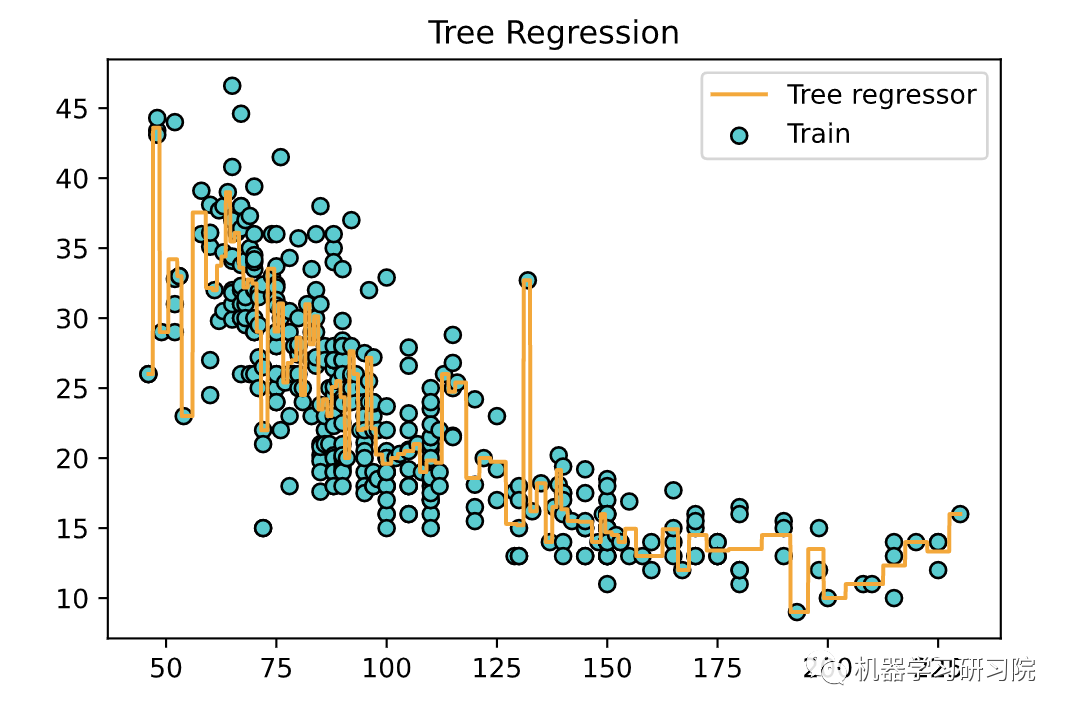
下面使用训练好的模型,绘制一条拟合曲线。```pythonX_grid = np.arange(min(X), max(X), 0.01)X_grid = X_grid.reshape(len(X_grid), 1)plt.scatter(X, y, color='DarkTurquoise',edgecolors='black', label='Train')plt.plot(X_grid, tree_regressor.predict(X_grid),color='orange', label='Tree regressor')plt.title('Tree Regression')plt.legend()plt.show()
小结
关于决策树的几个关键点:
- 易于理解和解释,并且决策树可以被可视化显示。
- 适用于离散值和连续值。
- 使用 DT预测数据的成本是训练树的训练数据对数量的对数。
- 决策树的预测既不平滑也不连续(显示为分段常数近似值,如上图所示)。
05 随机森林回归
一般地,随机森林回归与决策树回归非常相似,它是一个元估计器,在数据集的各种子样本集上拟合许多决策树,并使用平均方法来提高预测准确性和控制过拟合。
随机森林回归器在回归中的性能可能比决策树好,也可能不比决策树好(虽然它通常在分类中表现更好),因为树构造算法本质上存在微妙的过度拟合-欠拟合权衡。
随机森林回归很常见,以至于Scikit-learn内置了RandomForestRegressor. 首先,我们需要创建一个RandomForestRegressor具有指定数量估计器的对象,如下所示: ```python from sklearn.ensemble import RandomForestRegressor
forest_regressor = RandomForestRegressor( n_estimators = 300, random_state = 0 ) forest_regressor.fit(X, y.ravel())
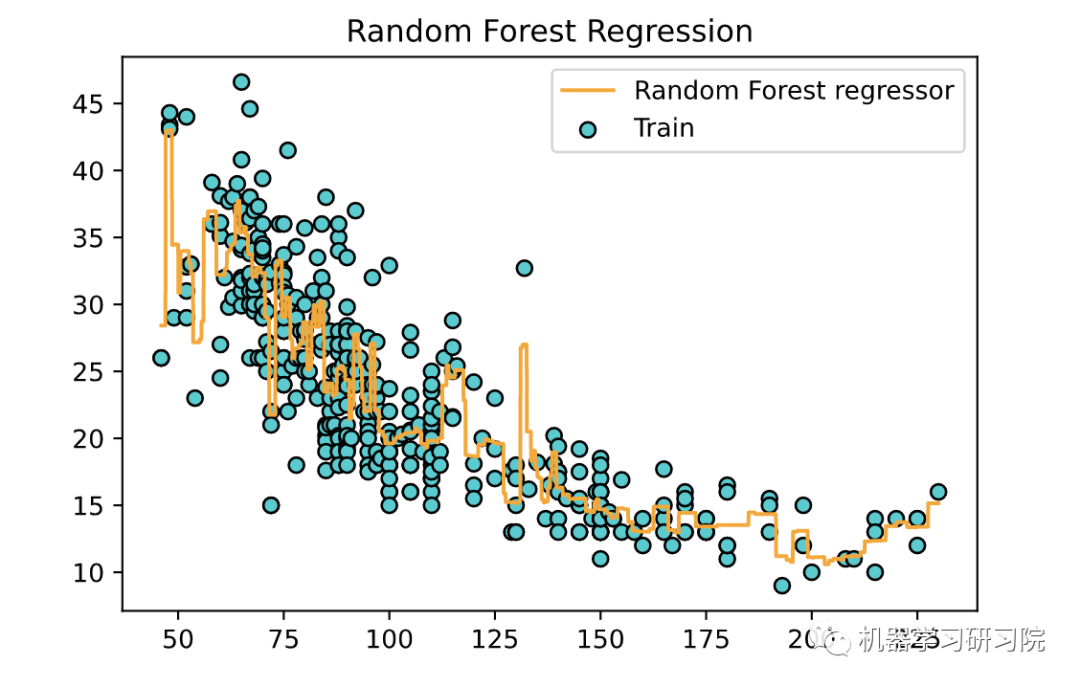
下面使用训练好的模型,绘制一条拟合曲线。```pythonX_grid = np.arange(min(X), max(X), 0.01)X_grid = X_grid.reshape(len(X_grid), 1)plt.scatter(X, y, color='DarkTurquoise',edgecolors='black', label='Train')plt.plot(X_grid, forest_regressor.predict(X_grid),color='orange', label='Random Forest regressor')plt.title('Random Forest Regression')plt.legend()plt.show()
小结
关于随机森林回归的几个关键点:
- 需要注意减少决策树中的过拟合并提高准确性
- 它也适用于离散值和连续值
- 需要大量的计算能力和资源,因为它适合许多决策树来组合它们的输出
06 LASSO 回归
LASSO 回归是使用收缩的线性回归的变体。收缩是数据值向中心点收缩作为均值的过程。这种类型的回归非常适合显示重度多重共线性(特征彼此之间的重度相关性)的模型。
Scikit-learn内置了LassoCV.from sklearn.linear_model import LassoCVlasso = LassoCV()lasso.fit(X, y.ravel())
下面使用训练好的模型,绘制一条拟合曲线。
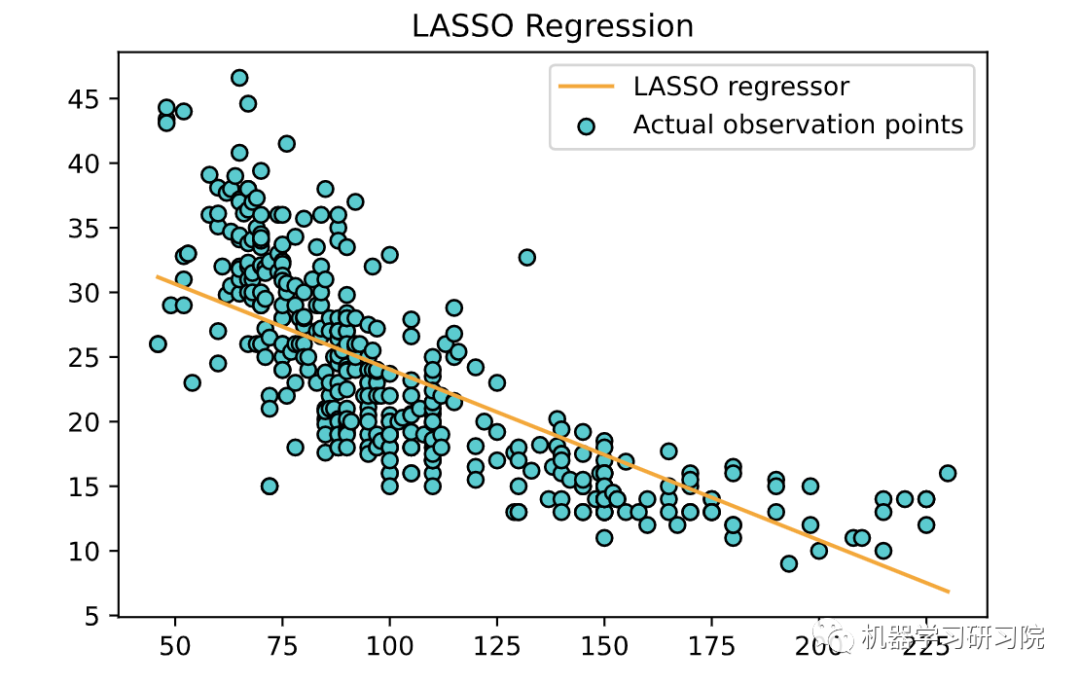
plt.scatter(X, y, color='teal', edgecolors='black',label='Actual observation points')plt.plot(X, lasso.predict(X), color='orange',label='LASSO regressor')plt.title('LASSO Regression')plt.legend()plt.show()
小结
关于套索回归的几点:
- 它最常用于消除自动化变量和选择特征。
- 它非常适合显示严重多重共线性(特征彼此高度相关)的模型。
- LASSO 回归利用 L1 正则化
- LASSO 回归被认为比 Ridge 更好,因为它只选择一些特征并将其他特征的系数降低到零。
07 岭回归
岭回归与 LASSO 回归非常相似,因为这两种技术都使用收缩。Ridge 回归和 LASSO 回归都非常适合显示重度多重共线性(特征彼此之间的高度相关性)的模型。它们之间的主要区别在于 Ridge 使用 L2 正则化,这意味着没有一个系数像在 LASSO 回归中那样变为零(而是接近零)。from sklearn.linear_model import RidgeCVridge = RidgeCV()ridge.fit(X, y)
下面使用训练好的模型,绘制一条拟合曲线。
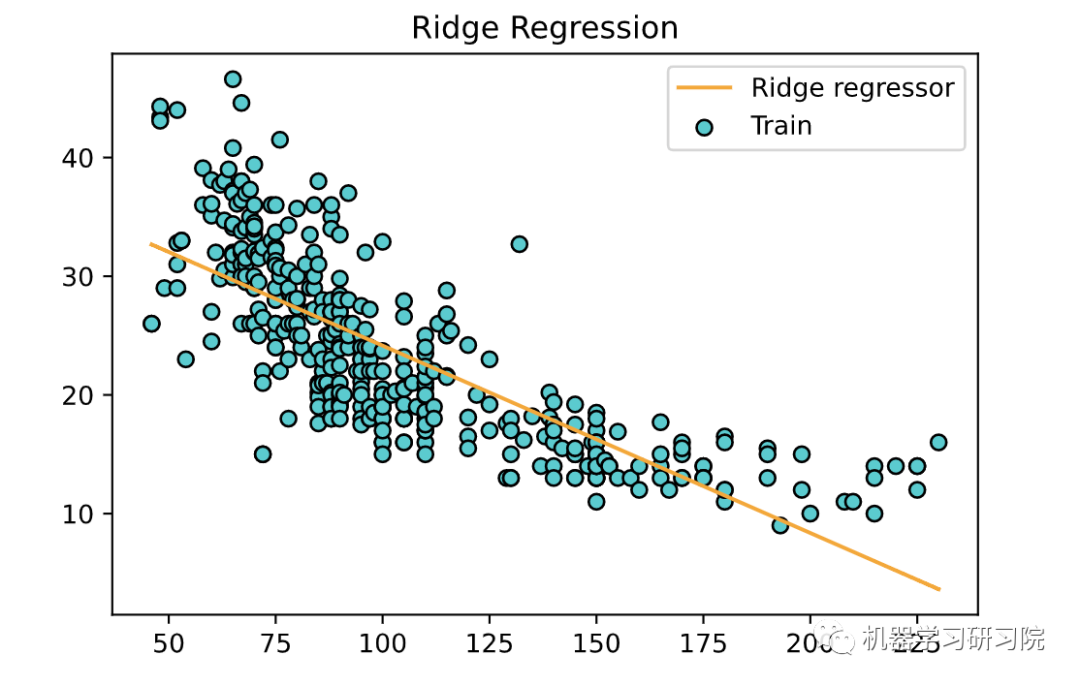
plt.scatter(X, y, color='teal', edgecolors='black',label='Train')plt.plot(X, ridge.predict(X), color='orange',label='Ridge regressor')plt.title('Ridge Regression')plt.legend()plt.show()
小结
关于岭回归的几个关键点:
- 它非常适合显示严重多重共线性(特征彼此高度相关)的模型。
- 岭回归使用 L2 正则化,贡献较小的特征将具有接近零的系数。
- 由于 L2 正则化的性质,岭回归被认为比 LASSO 差
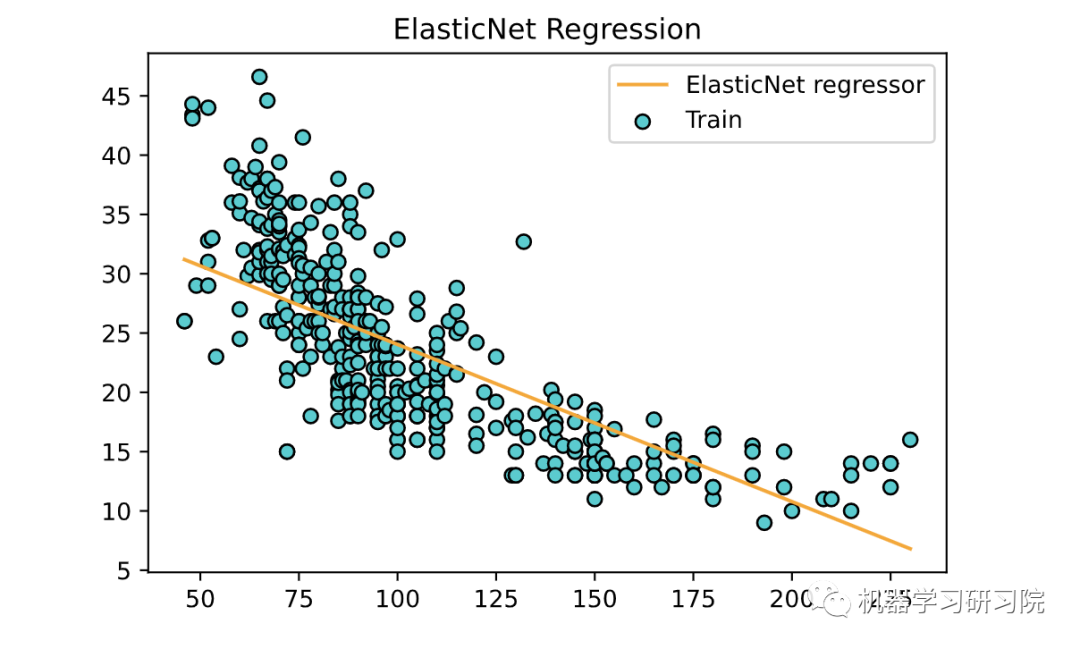
08 ElasticNet 回归
ElasticNet 是另一个使用 L1 和 L2 正则化训练的线性回归模型。它是 LASSO 和岭回归技术的混合体,因此它也非常适合显示严重多重共线性(特征彼此高度相关)的模型。
Lasso 和 Ridge 之间权衡的一个实际优势是它允许 Elastic-Net 在旋转时继承一些 Ridge 的稳定性。
Scikit-learn内置了ElasticNetCV模型.from sklearn.linear_model import ElasticNetCVelasticNet = ElasticNetCV()elasticNet.fit(X, y.ravel())
下面使用训练好的模型,绘制一条拟合曲线。
plt.scatter(X, y, color='DarkTurquoise', edgecolors='black', label='Train')plt.plot(X, elasticNet.predict(X), color='orange',label='ElasticNet regressor')plt.title('ElasticNet Regression')plt.legend()plt.show()
小结
ElasticNet 回归的几个关键点:
- ElasticNet 总是优于 LASSO 和 Ridge,因为它解决了两种算法的缺点
- ElasticNet 带来了额外的开销,用于确定最佳解决方案的两个 lambda 值。
09 XGBoost 回归
极限梯度提升( XGBoost ) 是梯度提升算法的高效实现。梯度提升是指一类可用于分类或回归问题的集成机器学习算法。
XGBoost是由最初开发的开放源码库tianqi-chen[3]在他的题为“2016论文XGBoost:可扩展树增压系统[4]”。该算法被设计为具有计算效率和高效性。
第一步是安装 XGBoost 库(如果尚未安装)。pip install xgboost
可以通过创建以下实例来定义 XGBoost 模型XGBRegressor:
from xgboost import XGBRegressor# create an xgboost regression modelmodel = XGBRegressor(n_estimators=1000,max_depth=7,eta=0.1,subsample=0.7,colsample_bytree=0.8,)model.fit(X, y)
- n_estimators:整体中的树木数量,通常会增加,直到看不到进一步的改进。
- max_depth:每棵树的最大深度,通常值在 1 到 10 之间。
- eta:用于对每个模型进行加权的学习率,通常设置为较小的值,例如 0.3、0.1、0.01 或更小。
- subsample:每棵树使用的样本数,设置为0到1之间的值,通常为1.0以使用所有样本。
- colsample_bytree:每棵树中使用的特征(列)数,设置为 0 到 1 之间的值,通常为 1.0 以使用所有特征。
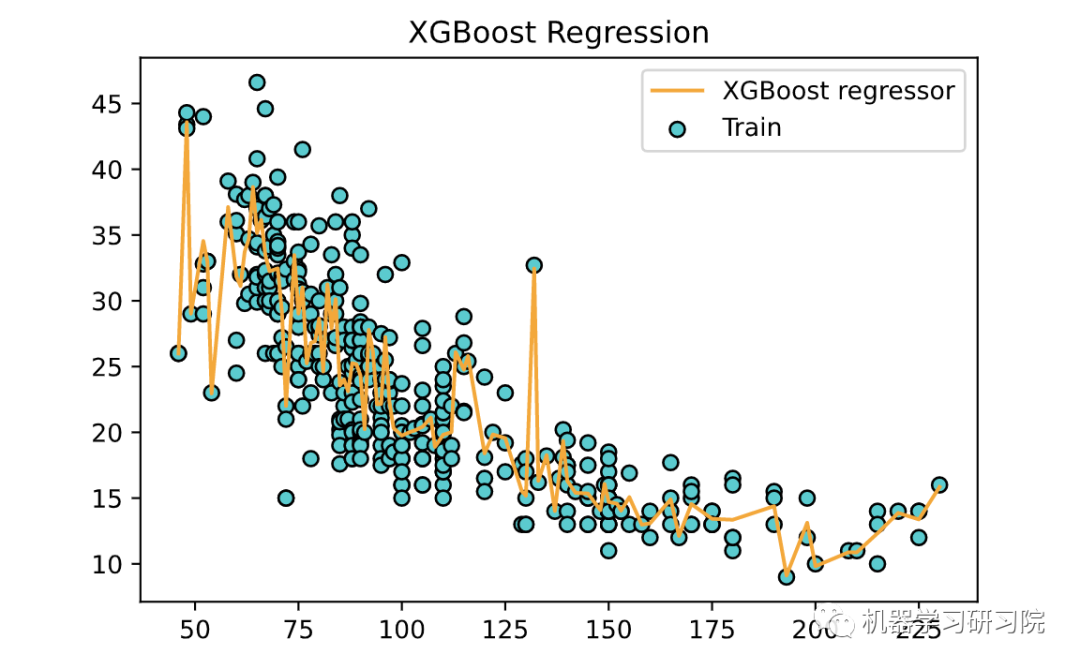
下面使用训练好的模型,绘制一条拟合曲线。
plt.scatter(X, y, color='DarkTurquoise', edgecolors='black', label='Train')plt.plot(X, model.predict(X), color='orange',label='XGBoost regressor')plt.title('XGBoost Regression')plt.legend()plt.show()
小结
关于 XGBoost 的几个关键点:
- XGBoost 在稀疏和非结构化数据上表现不佳。
- 该算法旨在计算高效且高效,但对于大型数据集而言,训练时间仍然相当长
- 对异常值很敏感
写在最后
到这里本文就结束啦,本文我们通过使用Scikit-learn和 XGBoost 的动手实践介绍了 九种流行的回归算法。在解决实际问题时,可以尝试不同的算法并找到解决实际问题的最佳回归模型。参考资料
[1][2][3][4]
参考原文: https://towardsdatascience.com/a-practical-introduction-to-9-regression-algorithms-389057f86eb9
Scikit-learn: https://scikit-learn.org/stable/
tianqi-chen: https://www.linkedin.com/in/tianqi-chen-679a9856/
可扩展树增压系统: https://arxiv.org/abs/1603.02754