参考资料：多项式回归处理非线性问题

多项式回归是一种通过增加自变量上的次数，而将数据映射到高维空间的方法，从而提高模型拟合复杂数据的效果。

线性模型中的升维工具——多项式变化。是一种通过增加自变量上的次数，而将数据映射到高维空间的方法，在sklearn中的PolynomialFeatures 设定一个自变量上的次数(大于1)，相应地获得数据投影在高次方的空间中的结果。

语法：

  1. sklearn.preprocessing.PolynomialFeatures (degree=2, interaction_only=False, include_bias=True)

重要参数：

  1. degree : integer
  2. 多项式中的次数，默认为2
  3. interaction_only : boolean, default = False
  4. 布尔值是否只产生交互项，默认为False。就只能将原有的特征进行组合出新的特征，而不能直接对原特征进行升次。
  5. include_bias : boolean
  6. 布尔值，是否产出与截距项相乘的 ，默认True

案例一、拟合正弦曲线

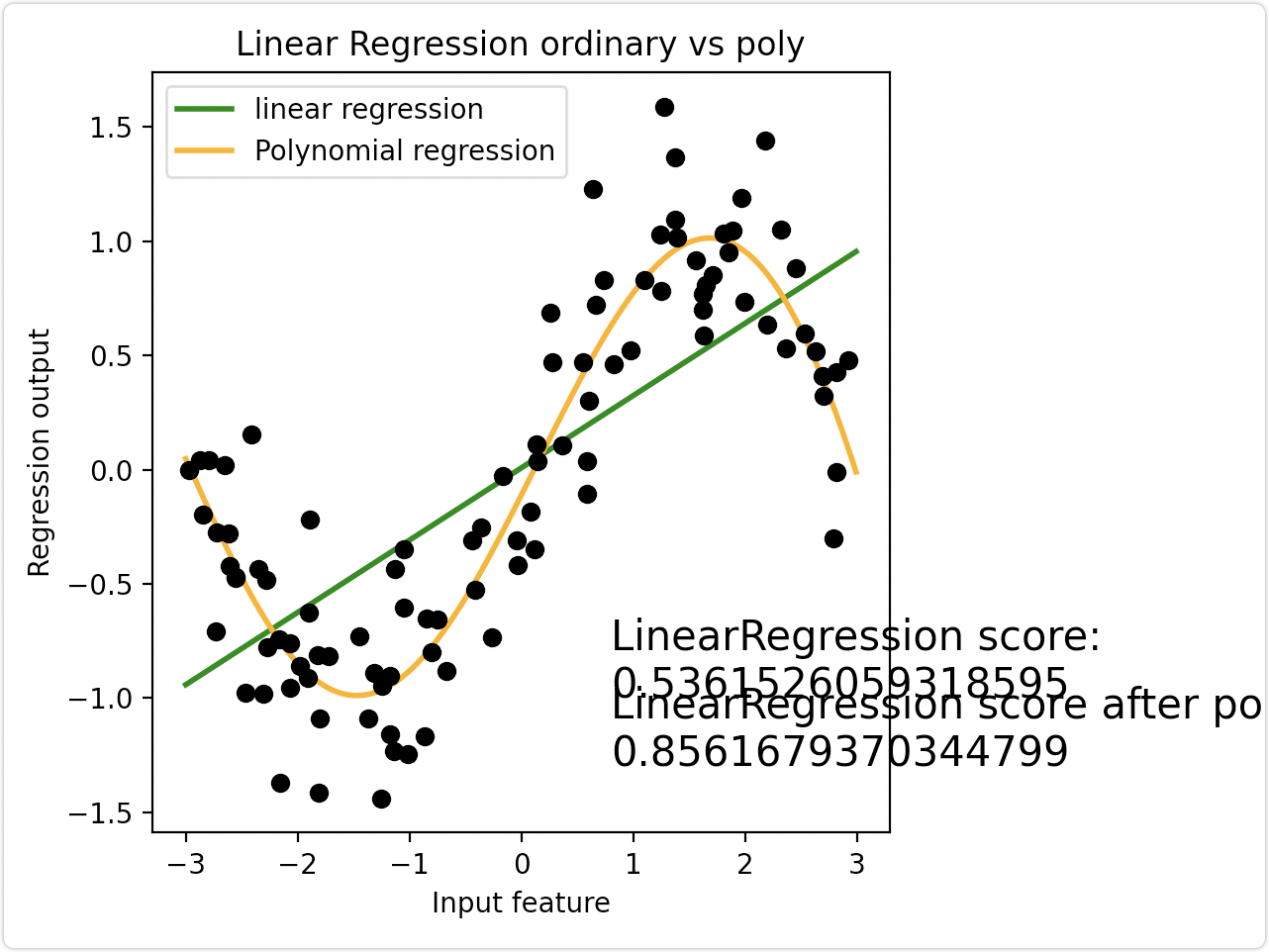
线性回归模型无法拟合出这条带噪音的正弦曲线的真实面貌，只能够模拟出大概的趋势，而用复杂的决策树模型又拟合地太过细致，即过拟合。此时利用多项式将数据升维，并拟合数据

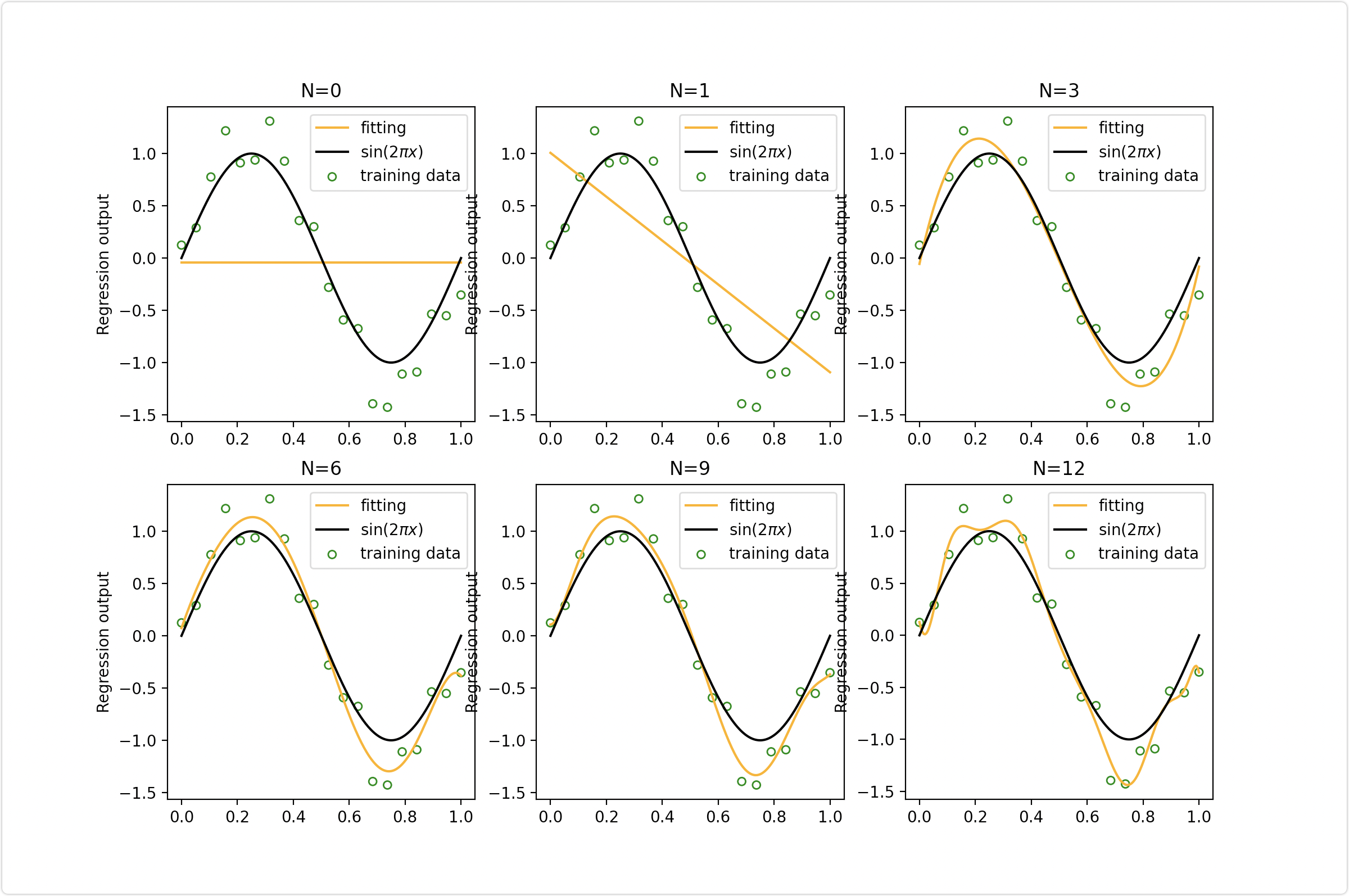
image.png

案例二、不同的最高次取值对拟合效果的影响

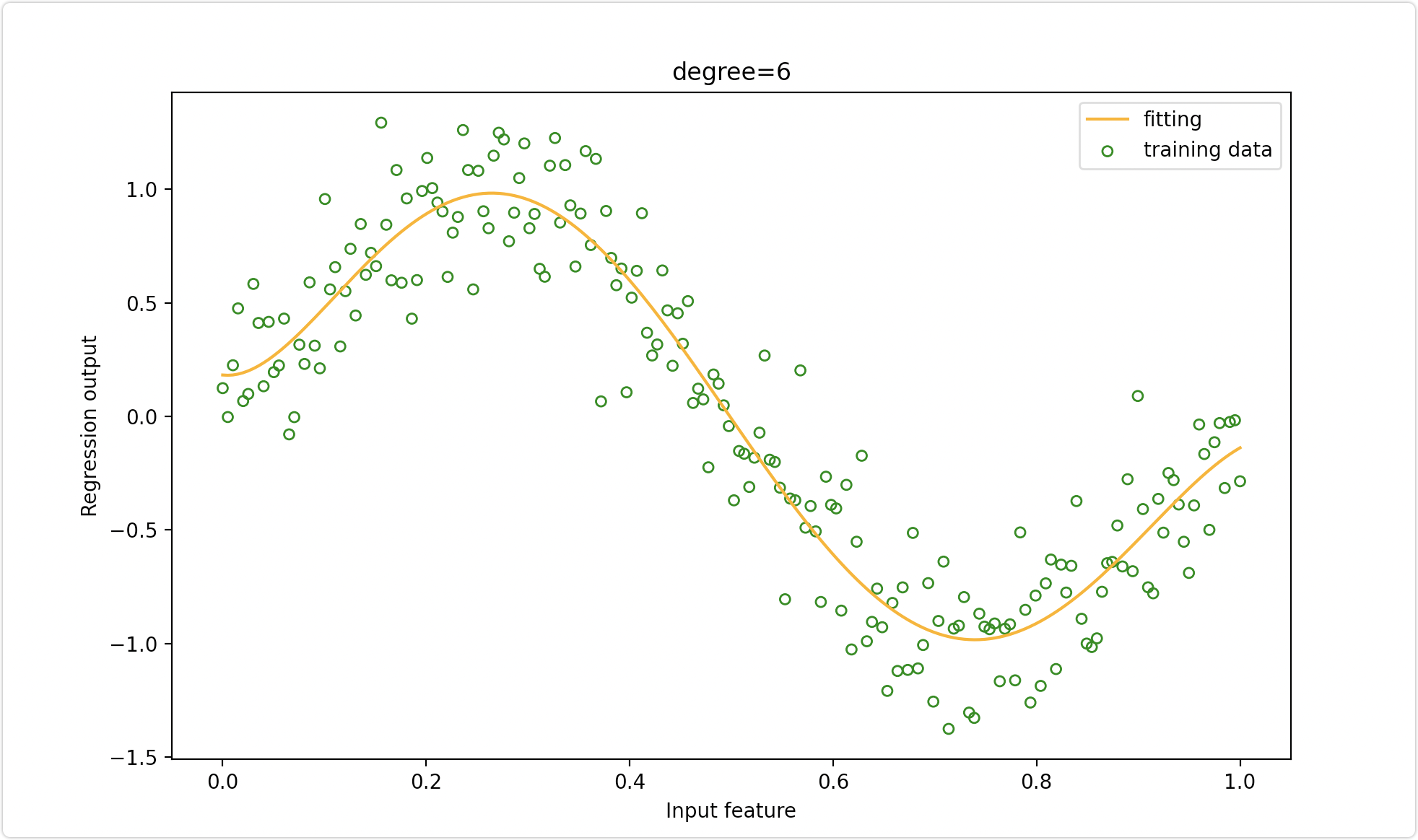
image.png

案例三、利用pipeline将三个模型封装起来串联操作

image.png

完整代码：

https://github.com/SeafyLiang/machine_learning_study/blob/master/regression/polynomialFeatures.py

  1. from sklearn.pipeline import Pipeline
  2. from sklearn.preprocessing import PolynomialFeatures as PF, StandardScaler
  3. from sklearn.linear_model import LinearRegression
  4. import numpy as np
  5. import matplotlib.pyplot as plt
  8. def demo1():
  9.     '''
  10.     利用多项式将数据升维，并拟合数据
  11.     '''
  12.     rnd = np.random.RandomState(42)  # 设置随机数种子
  13.     X = rnd.uniform(-3, 3, size=100)
  14.     y = np.sin(X) + rnd.normal(size=len(X)) / 3
  15.     # 将X升维，准备好放入sklearn中
  16.     X = X.reshape(-1, 1)
  17.     # 多项式拟合，设定高次项
  18.     d = 5
  19.     # 原始特征矩阵的拟合结果
  20.     LinearR = LinearRegression().fit(X, y)
  21.     # 进行高此项转换
  22.     X_ = PF(degree=d).fit_transform(X)
  23.     LinearR_ = LinearRegression().fit(X_, y)
  24.     line = np.linspace(-3, 3, 1000, endpoint=False).reshape(-1, 1)
  25.     line_ = PF(degree=d).fit_transform(line)
  26.     # 放置画布
  27.     fig, ax1 = plt.subplots(1)
  28.     # 将测试数据带入predict接口，获得模型的拟合效果并进行绘制
  29.     ax1.plot(line, LinearR.predict(line), linewidth=2, color='green'
  30.              , label="linear regression")
  31.     ax1.plot(line, LinearR_.predict(line_), linewidth=2, color='orange'
  32.              , label="Polynomial regression")  # 将原数据上的拟合绘制在图像上
  33.     ax1.plot(X[:, 0], y, 'o', c='k')
  34.     # 其他图形选项
  35.     ax1.legend(loc="best")
  36.     ax1.set_ylabel("Regression output")
  37.     ax1.set_xlabel("Input feature")
  38.     ax1.set_title("Linear Regression ordinary vs poly")
  39.     ax1.text(0.8, -1, f"LinearRegression score:\n{LinearR.score(X, y)}", fontsize=15)
  40.     ax1.text(0.8, -1.3, f"LinearRegression score after poly :\n{LinearR_.score(X_, y)}", fontsize=15)
  42.     plt.tight_layout()
  43.     plt.show()
  46. # 生产数据函数
  47. def uniform(size):
  48.     x = np.linspace(0, 1, size)
  49.     return x.reshape(size, 1)
  52. def create_data(size):
  53.     x = uniform(size)
  54.     np.random.seed(42)  # 设置随机数种子
  55.     y = sin_fun(x) + np.random.normal(scale=0.25, size=x.shape)
  56.     return x, y
  59. def sin_fun(x):
  60.     return np.sin(2 * np.pi * x)
  63. def demo2():
  64.     '''
  65.     不同的最高次取值，对模型拟合效果有重要的影响。
  66.     '''
  67.     X_train, y_train = create_data(20)
  68.     X_test = uniform(200)
  69.     y_test = sin_fun(X_test)
  70.     fig = plt.figure(figsize=(12, 8))
  71.     for i, degree in enumerate([0, 1, 3, 6, 9, 12]):
  72.         plt.subplot(2, 3, i + 1)
  74.         poly = PF(degree)
  75.         X_train_ploy = poly.fit_transform(X_train)
  76.         X_test_ploy = poly.fit_transform(X_test)
  78.         lr = LinearRegression()
  79.         lr.fit(X_train_ploy, y_train)
  80.         y_pred = lr.predict(X_test_ploy)
  82.         plt.scatter(X_train, y_train, facecolor="none", edgecolor="g", s=25, label="training data")
  83.         plt.plot(X_test, y_pred, c="orange", label="fitting")
  84.         plt.plot(X_test, y_test, c="k", label="$\sin(2\pi x)$")
  85.         plt.title("N={}".format(degree))
  86.         plt.legend(loc="best")
  87.         plt.ylabel("Regression output")
  88.         #     plt.xlabel("Input feature")
  89.         plt.legend()
  90.     plt.show()
  93. def demo3():
  94.     '''
  95.     利用pipeline将三个模型封装起来串联操作，让模型接口更加简洁，使用起来方便
  96.     '''
  97.     X, y = create_data(200)  # 利用上面的生产数据函数
  98.     degree = 6
  99.     # 利用Pipeline将三个模型封装起来串联操作n
  100.     poly_reg = Pipeline([
  101.         ("poly", PF(degree=degree)),
  102.         ("std_scaler", StandardScaler()),
  103.         ("lin_reg", LinearRegression())
  104.     ])
  105.     fig = plt.figure(figsize=(10, 6))
  106.     poly = PF(degree)
  107.     poly_reg.fit(X, y)
  108.     y_pred = poly_reg.predict(X)
  109.     # 可视化结果
  110.     plt.scatter(X, y, facecolor="none", edgecolor="g", s=25, label="training data")
  111.     plt.plot(X, y_pred, c="orange", label="fitting")
  112.     # plt.plot(X,y,c="k",label="$\sin(2\pi x)$")
  113.     plt.title("degree={}".format(degree))
  114.     plt.legend(loc="best")
  115.     plt.ylabel("Regression output")
  116.     plt.xlabel("Input feature")
  117.     plt.legend()
  118.     plt.show()
  121. if __name__ == '__main__':
  122.     demo1()
  123.     demo2()
  124.     demo3()