参考资料： 基于数据驱动的电动汽车行驶里程模型建立与分析 python怎么计算相关系数、偏相关系数？ 利用PYTHON计算偏相关系数（Partial correlation coefficient)

一、需求场景

新能源电动车剩余里程预测

我们都知道，影响行驶里程的因素有很多，包括电池的剩余电量、电池性能(电池组放电总电压、电池组电池不一致性、单体电压、电池组内阻)、整车参数、车辆载重、车辆行驶特性及温度等因素。

针对电池性能（SOC、电压、电流和电池温度）和车辆行驶特性（速度）几个方面进行深入研究，实现行驶里程估计，从而达到预测剩余里程的目的。

二、偏相关分析简介

2.1 引入偏相关分析的原因

相关分析是处理变量与变量之间关系的一种统计方法，

2.1.1 从所处理的变量多少来看，

如果研究的是两个变量间的关系称为简单相关；
如果研究的是两个以上变量间的关系称为多元相关。

2.1.2 从变量之间的关系形式上看，有

线性相关分析；
非线性相关分析。

2.1.3 从统计思想和方法来看，

线性相关是最基本的方法。

在相关分析中，研究两事物之间的线性相关性是通过计算相关系数等方式实现，并通过相关系数值的大小来判定事物之间的线性相关强弱。

详细内容：
数据挖掘01-相关性分析及可视化【Pearson, Spearman, Kendall】

然而，当简单相关系数受其他因素的影响，它所反映的往往是表面的非本质的联系。此时要准确地反映两个变量之间的内在联系，就不能简单的计算相关系数，而是需要考虑偏相关系数。

2.2 什么是偏相关分析

偏相关分析也称净相关分析，它在控制其他变量的线性影啊的条件下分析两变量间的线性关系，通常用偏相关系数(即净相关系数)表示。

当控制变量个数为一时，偏相关系数称为一阶偏相关；
当控制变量个数为二时，偏相关系数称为二阶偏相关：
当控制变量个数为零时，偏相关系数称为零阶偏相关，即简单相关系数。

偏相关系数是在对其他变量的影响进行控制的条件下，衡量多个变量中某两个变量之间的线性相关程度的指标。所以，用偏相关系数来描述两个经济变量之间的内在线性联系会更合理、更可靠。

偏相关系数不同于简单相关系数，在计算偏相关系数时，需要掌握多个变量的数据，
一方面考虑多个变量之间可能产生的影响，另一方面又采用一定的方法控制其他变量，专门考察两个特定变量的净相关关系。

在多变量相关的场合，出于变量之间存在错综复杂的关系，因此偏相关系数与简单相关系数在数值上可能相差很大，有时甚至符号都可能相反。偏相关系数取值范围与简单相关系数一样，为-1到1。偏相关系数绝对值越大(越接近1)，表明变量之间的线性相关程度越高；偏相关系数绝对值越小(越接近0)，表明变量之间的线性相关程度越低。

2.3 偏相关分析的步骤

利用偏相关系数进行变量间净关系分析通常需要完成以下两大步骤：

（1）计算样本的偏相关系数

利用样本数据计算样本的偏相关系数，它反映了两变量间净相关的程度强弱。在分析变量x1和y1之间的净相关时，当控制了x2的线性作用后，x1和y1之间的一阶相关系数定义为：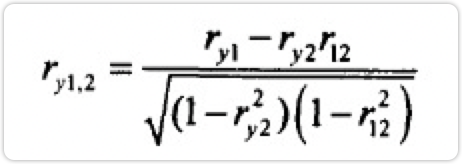
image.png
ry1、ry2、r12分别表示y和x1的相关系数、y和x2的相关系数、x1和x2的简单相关系数

（2）对上一步求得的偏相关系数进行检验

净相关分析检验的基本步骤是：

  1.   1. **提出假设**，假设偏相关系数与零无显著性差异，即两个变量之间不线性相关。
  2.   1. **选择检验统计量**。偏相关分析的检验统计量为t统计量，它的数学定义为：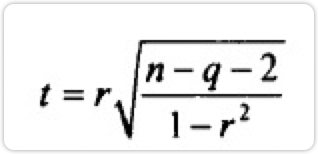
  3.      1. ![image.png](https://cdn.nlark.com/yuque/0/2021/png/2524844/1638369971471-78d2338e-6f8e-4864-a772-4dfb58739f7a.png#clientId=u4793cd87-12fd-4&from=paste&height=77&id=u6c8ff0a4&margin=%5Bobject%20Object%5D&name=image.png&originHeight=154&originWidth=318&originalType=binary&ratio=1&size=34807&status=done&style=none&taskId=u01ad8ea4-9df6-4cf0-b3c1-51ce5ec3637&width=159)
  4.      1. r为偏相关系数，n为样本数，q为阶数。t统计量服从n-q-2个自由度的t分布。
  5.   3. **计算检验统计量的观测值和对应的概率p值**。
  6.   3. **决策**。如果检验统计量的概率p值小于给定的显著性水平α（一般为0.05），应拒绝零假设，认为两总体的偏相关系数与零有显著性差异，即两变量之间有显著的线性相关关系；反之，如果检验统计量的概率p值大于给定的显著性水平α，则说明两变量之间没有显著线性相关关系。

三、【案例分析】行驶里程与影响因素的偏相关分析

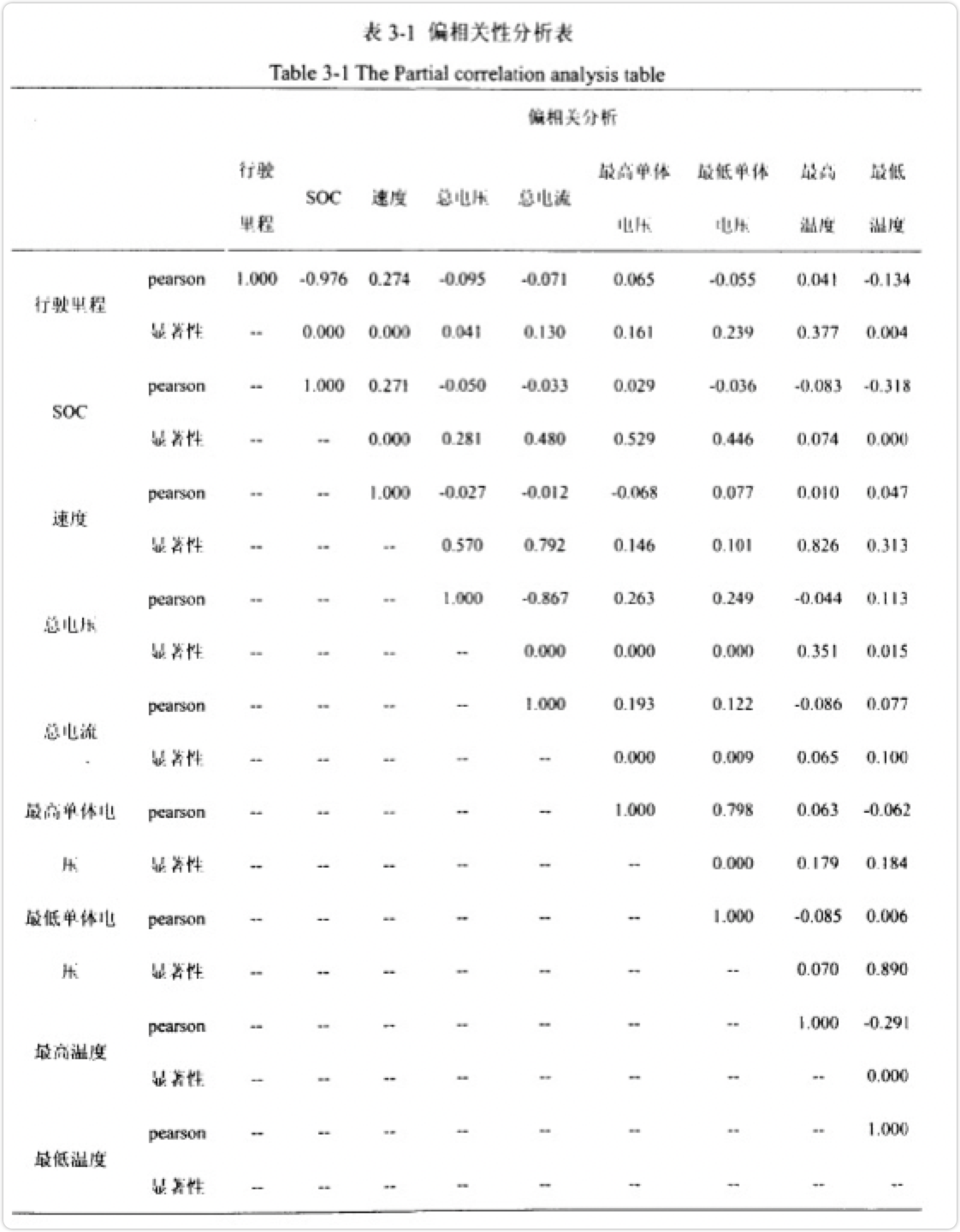
image.png
由上表3-1可知，行驶里程和电池SOC的Pearson相关系数为-0.976，相关系数检验的概率p值都近似为0，说明两者之间具有很强的负线性相关关系，而其他变量与行驶里程之间的Pearson相关系数都偏小，说明他们之间的线性相关性并不明显，说明这些影响因素可能是通过非线性关系来影响行驶里程的变化的。

3.1 速度

为了分析电动车行驶速度和里程之间的关系，将【车速、soc、行驶里程】绘制曲线图进行分析：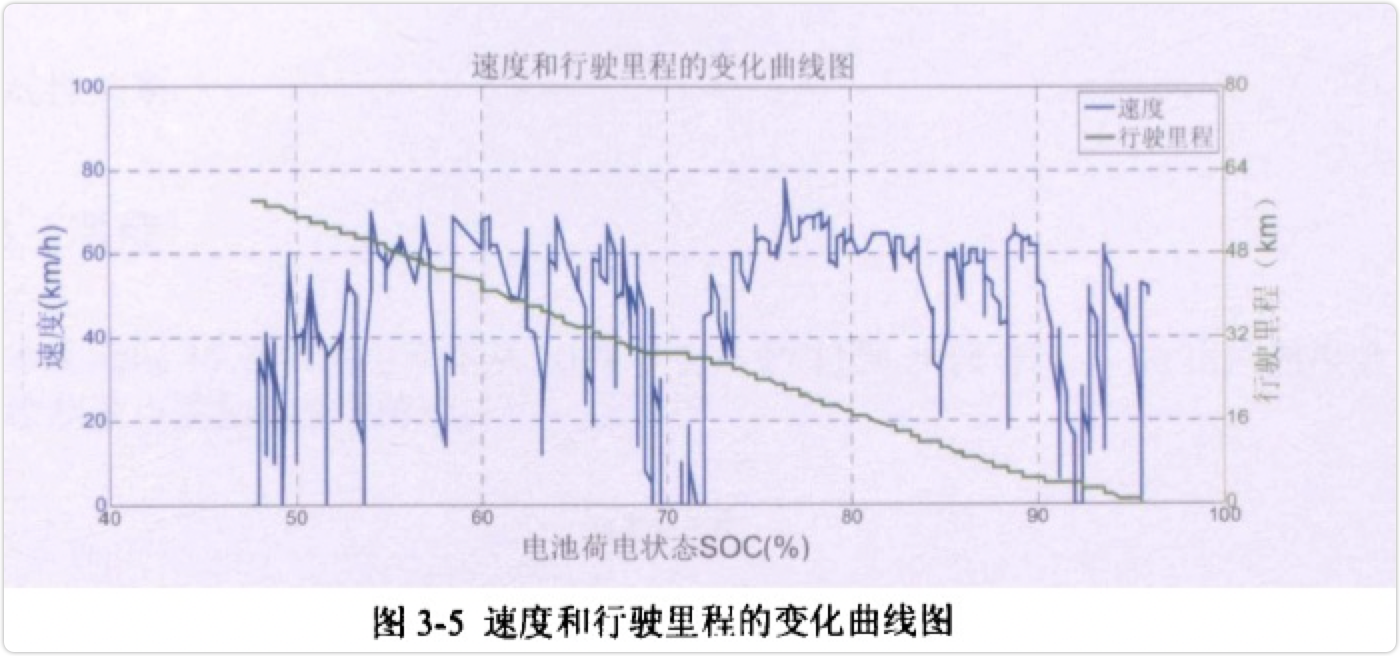
image.png
图3-5为速度和形式里程的变化曲线图，从图中可以看出，速度的曲线上下波动较大。电池SOC从96%下降到47%的过程中，当速度为0时，行驶里程曲线为水平走向，说明此刻车辆处在停止状态，当速度不为0时，行驶里程开始逐渐增加，说明速度对行驶里程有很大影响。但是由之前的偏相关分析表3-1可知，速度和里程之间不是线性关系，因此采用每公里电量消耗百分比来分析。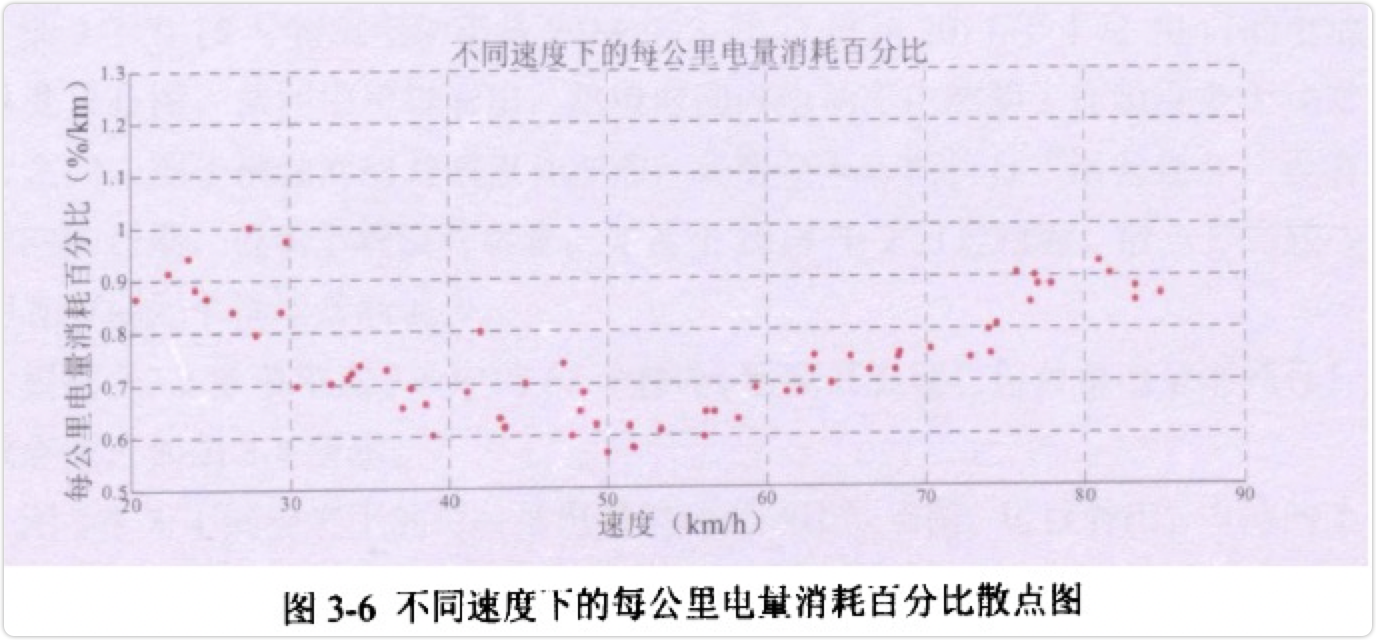
image.png
图3-6为不同速度下的每公里电量消耗百分比散点图，从图中可以看出，速度从20km/h变化到90km/h的过程中，每公里电量消耗百分比是由大变小再变大，当速度为50%左右的时候，每公里电量消耗百分比会达到最小值。由此可以看出，速度对每公里电量消耗百分比影响显著，并通过影响每公里电量消耗百分比的形式来影响行驶里程的。从图中可以看出速度对每公里电量消耗百分比的影响呈现非线性关系。

3.2 温度

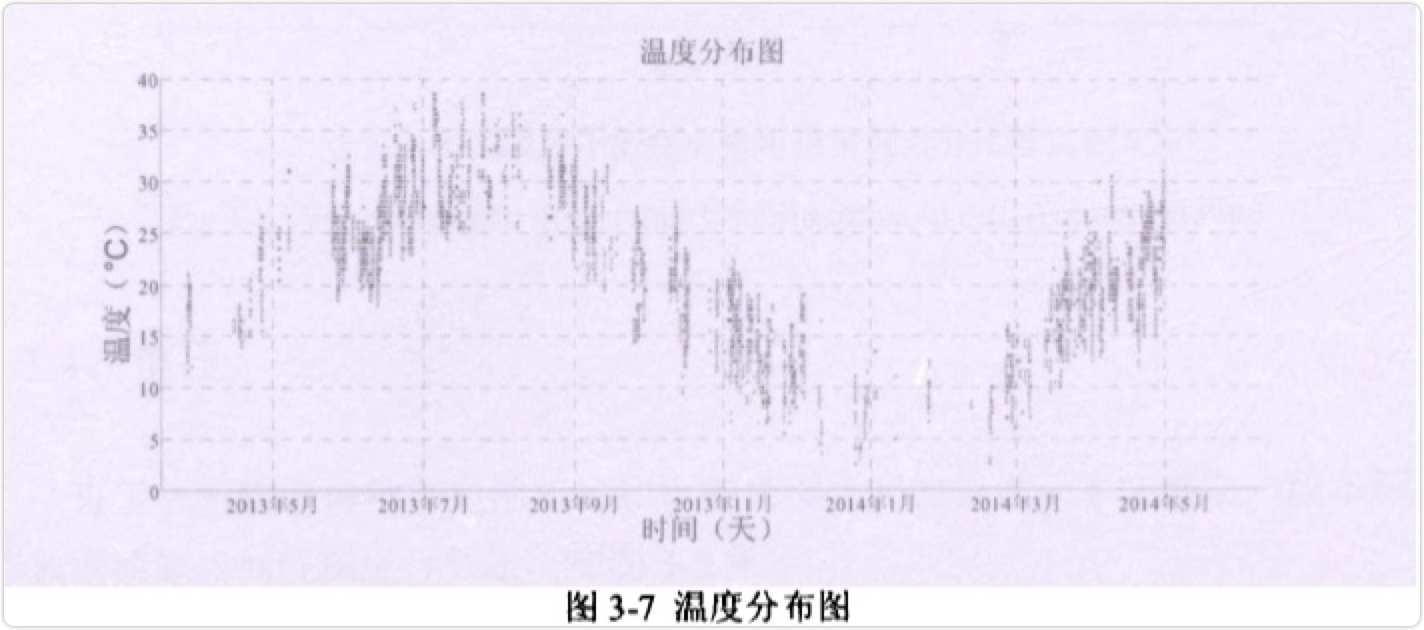
image.png
图3-7为电动车的电池放电温度分布图，从图中可以看出，这段时间内电动车电池的工作温度处于0℃到 40℃之间。图中横轴对应有散点存在的，说明今天车辆有出行；没有散点对应的日期，说明车辆没有出行。尤其在2014年2月份附近，散点分布较少， 说明春节期间车辆出行活动少。

与速度同理，绘制其温度与每公里电量消耗百分比的散点图，如图3-8所示。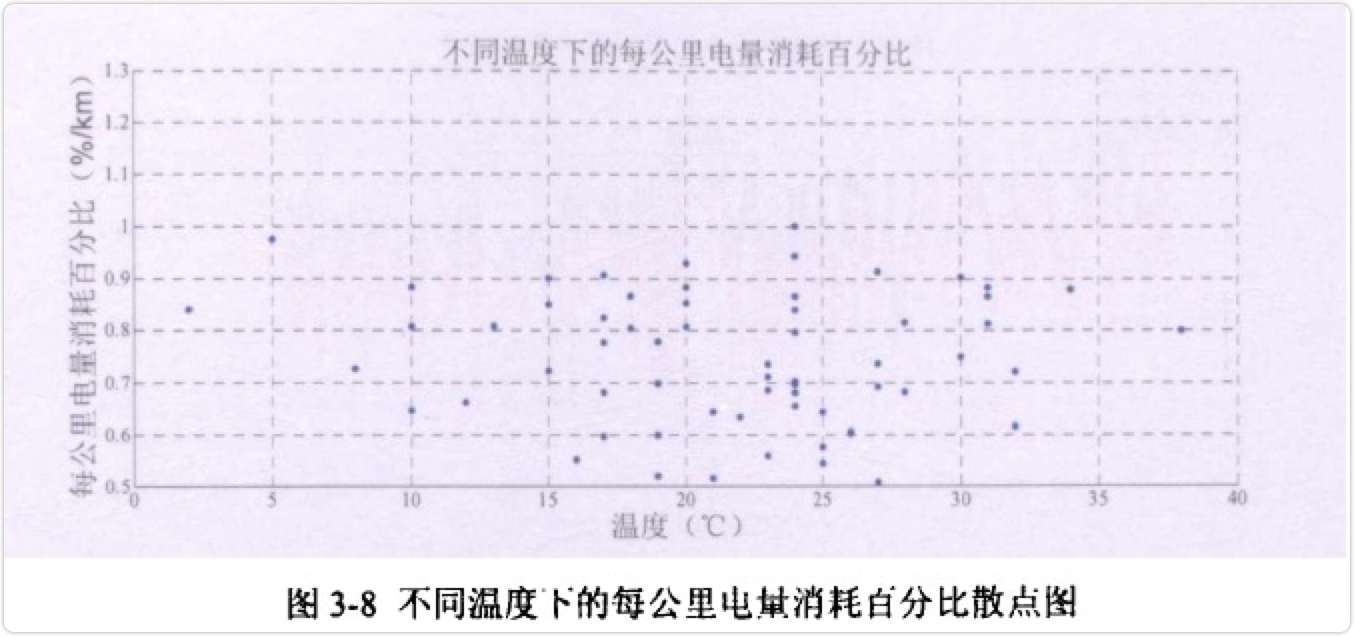
image.png
图3-8为不同温度下的每公里电量消耗百分比散点图，可以看出，电池的工作温度为20℃左右的情况比较多。并且不同温度下对应的每公里电量消耗百分比都位于0.5至1之间。从图中并未发现温度对每公里电量消耗百分比存在明显的影响。

3.3 电压

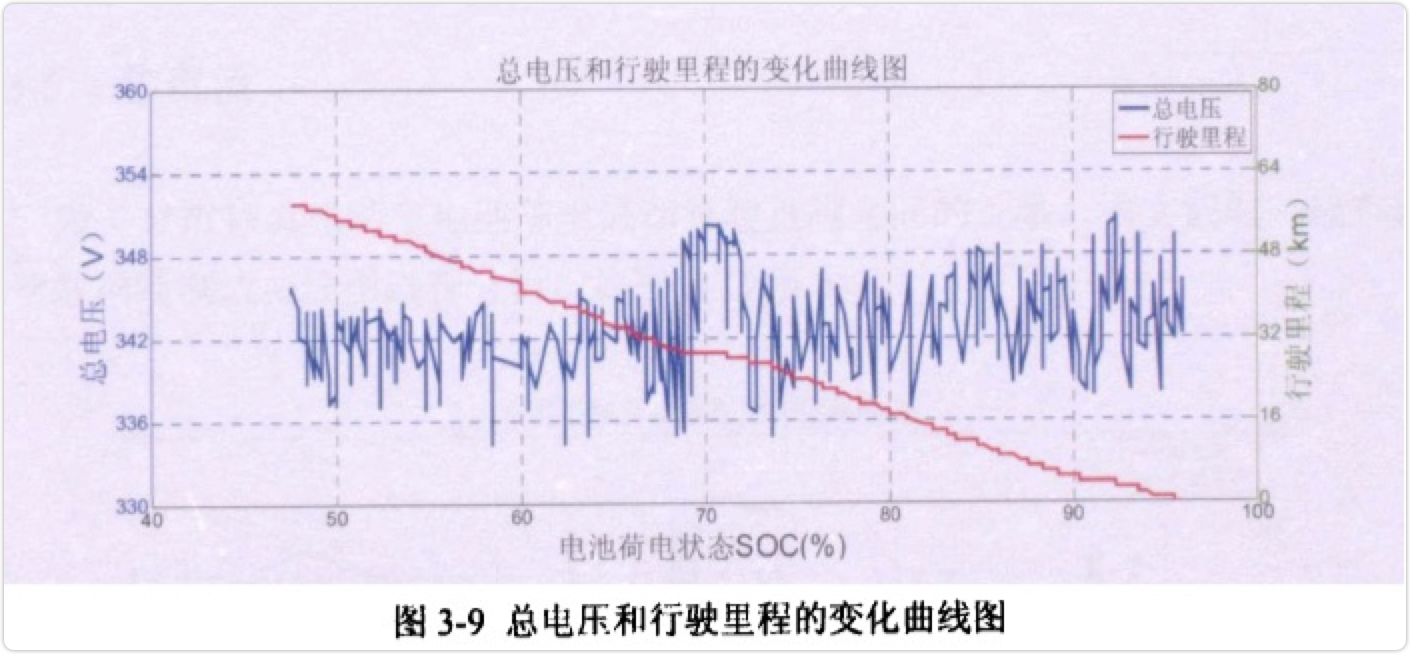
image.png
图3-9为电动车在一次放电过程中的行驶里程与总电压变化的曲线图。可以看出物理电动车在一次放电过程中，随着时间的推移总里程在增加，而总电压则是上下波动不定的，但是可以看出总电压值随着里程的增加略微有下降的趋势。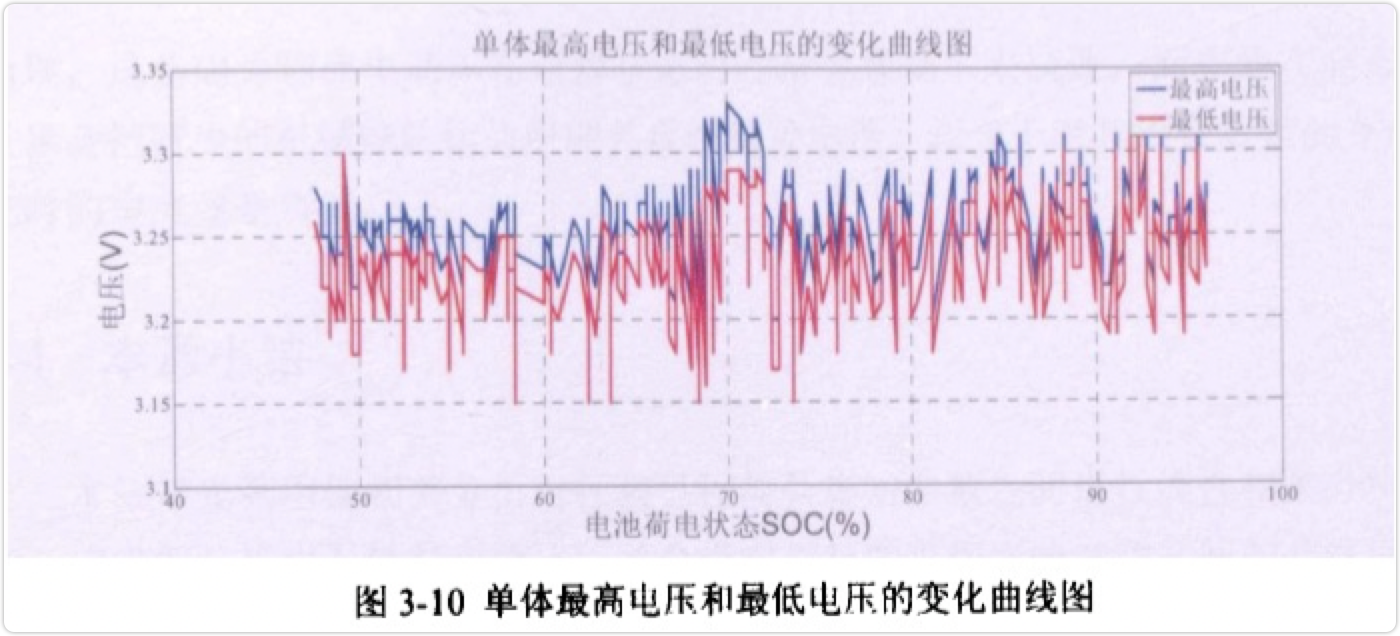
image.png
由图3-10可以看出，在一次放电过程中，单体电池的最高电压和最低电压也是上下波动的，波动的同时两条曲线的振动趋势具有很强的一致性，这应该是出于所有电池都串联在一起的缘故。另外，同总电压一样，随着电池SOC的减少里程数的增加，最高电压和最低电压也有略微下降的走势。

3.4 总电流

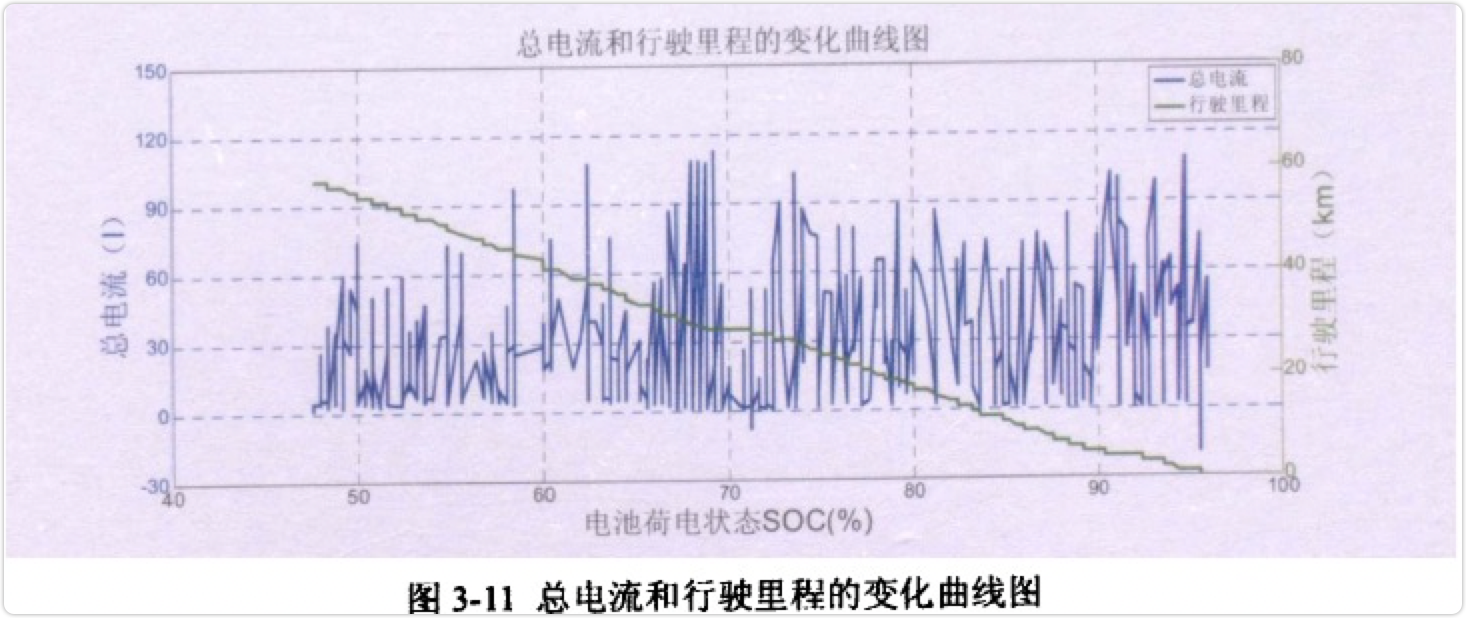
image.png
图3-11为电动车在出行过程中总电流和行驶里程的变化曲线图，从图中可以看出，车辆在放电过程中，电流并不是一直是正值，偶尔也会有负值的出现，这是因为电动车在出行状态时经常会踩刹车来减速，而车辆在刹车的时候会把减少的机械能转化为电能并反馈给蓄电池，相当于对其进行短暂的充电， 此时的电流就是负值。

3.5 小结

利用偏相关分析对行驶里程与其影响参数之间进行线性相关分析，然后定义每公里电量消耗百分比，并分析它与行驶里程影响参数之间的非线性关 系。目的是为后面的模型建立时选择影响因素做基础。

四、python偏相关分析

4.1 数据源

  1. x1=np.random.rand(10)
  2. x2=np.random.rand(10)
  3. x3=np.random.rand(10)
  4. print(x1)
  5. print(x2)
  6. print(x3)

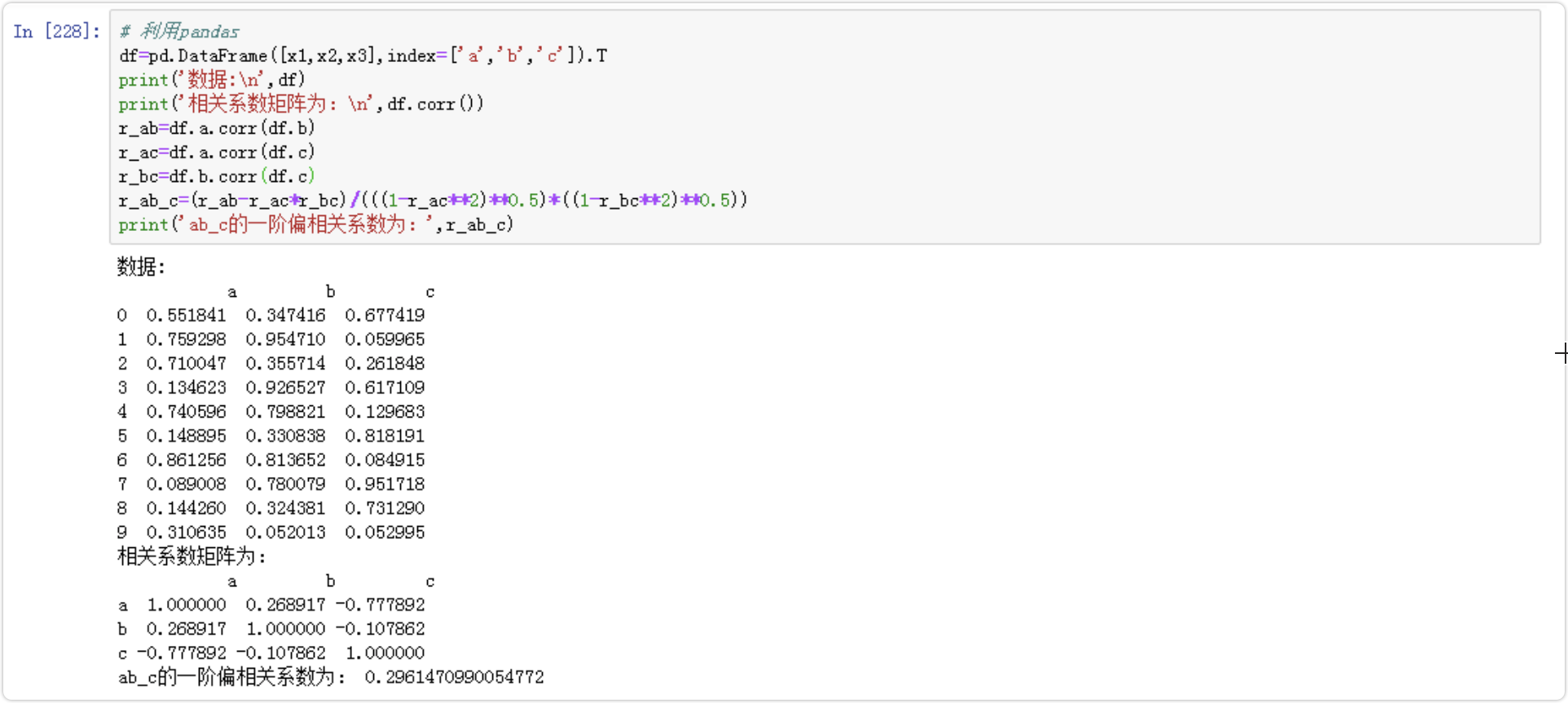
4.2 pandas

4.2.1 一阶相关系数

  1. # 利用pandas
  2. df=pd.DataFrame([x1,x2,x3],index=['a','b','c']).T
  3. print('数据:\n',df)
  4. print('相关系数矩阵为：\n',df.corr())
  5. r_ab=df.a.corr(df.b)
  6. r_ac=df.a.corr(df.c)
  7. r_bc=df.b.corr(df.c)
  8. r_ab_c=(r_ab-r_ac*r_bc)/(((1-r_ac**2)**0.5)*((1-r_bc**2)**0.5))
  9. print('ab_c的一阶偏相关系数为：',r_ab_c)

image.png

4.2.2 pcorr()

要一次性计算多个变量之间的部分相关性，可以使用.pcorr()函数:

  1. #calculate all pairwise partial correlations, rounded to three decimal places
  2. df.pcorr().round(3)
  4.          currentGrade    hours    examScore
  5. currentGrade        1.000      -0.311        0.736
  6. hours               -0.311    1.000        0.191
  7. examScore        0.736    0.191        1.000

4.3 numpy

  1. # 利用Numpy
  2. lst=[x1,x2,x3]
  3. res=np.corrcoef(lst)
  4. print('相关系数矩阵为：\n',res)
  5. label=['a','b','c']
  6. corr=dict()
  7. for row in range(res.shape[0]):
  8.     for col in range(res.shape[1]):
  9.         corr['r_{}{}'.format(label[row],label[col])]=res[row][col]
  10. r_ab=corr['r_ab']
  11. r_ac=corr['r_ac']
  12. r_bc=corr['r_bc']
  13. r_ab_c=(r_ab-r_ac*r_bc)/(((1-r_ac**2)**0.5)*((1-r_bc**2)**0.5))
  14. print('ab_c的一阶偏相关系数为：',r_ab_c)

image.png

4.4 sicpy

  1. # 利用sicpy
  2. from scipy import stats
  3. r_ab=stats.pearsonr(x1,x2)[0]
  4. r_ac=stats.pearsonr(x1,x3)[0]
  5. r_bc=stats.pearsonr(x2,x3)[0]
  6. r_ab_c=(r_ab-r_ac*r_bc)/(((1-r_ac**2)**0.5)*((1-r_bc**2)**0.5))
  7. print('ab_c的一阶偏相关系数为：',r_ab_c)

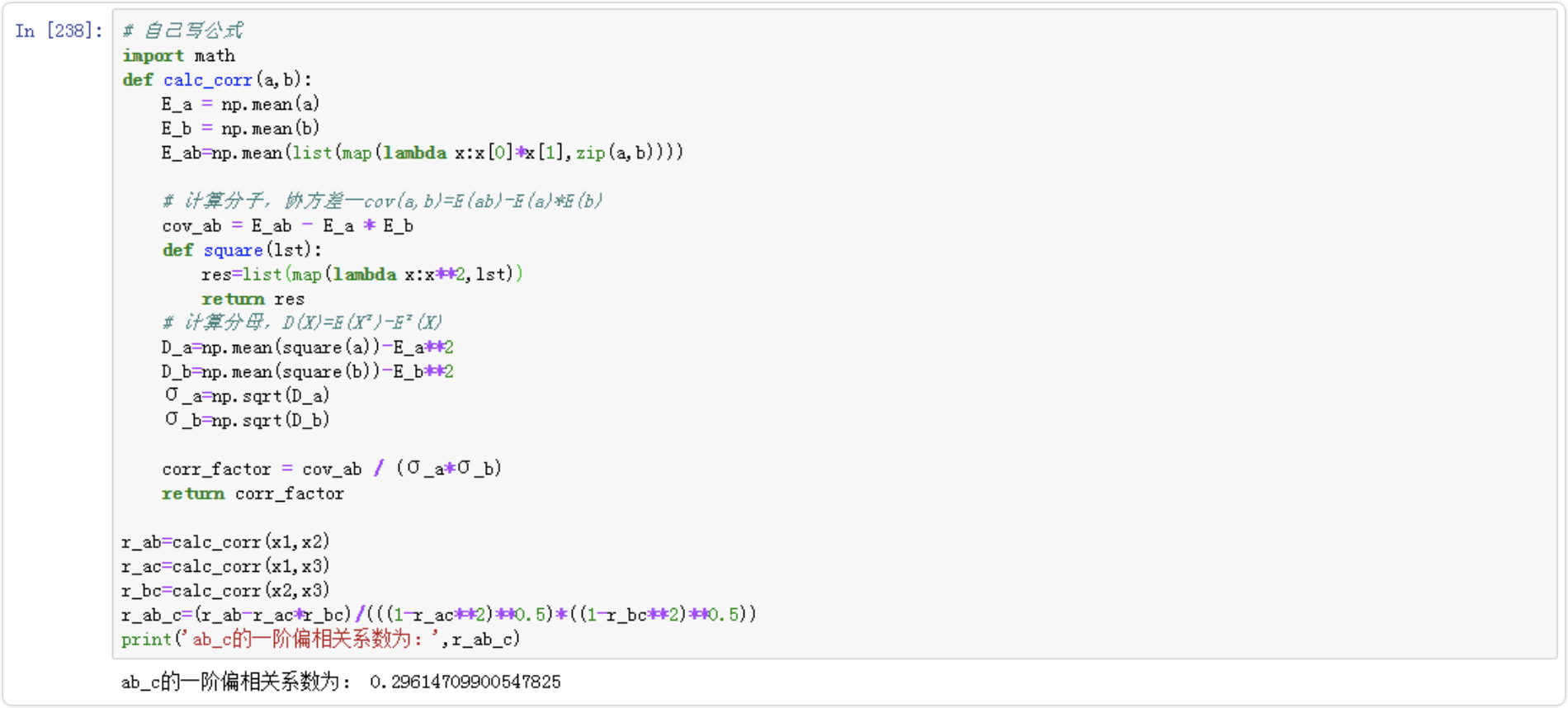
image.png

4.5 自己写公式

  1. # 自己写公式
  2. import math
  3. def calc_corr(a,b):
  4.     E_a = np.mean(a)
  5.     E_b = np.mean(b)
  6.     E_ab=np.mean(list(map(lambda x:x[0]*x[1],zip(a,b))))
  8.     # 计算分子，协方差—cov(a,b)=E(ab)-E(a)*E(b)
  9.     cov_ab = E_ab - E_a * E_b
  11.     def square(lst):
  12.         res=list(map(lambda x:x**2,lst))
  13.         return res
  15.     # 计算分母，D(X)=E(X²)-E²(X)
  16.     D_a=np.mean(square(a))-E_a**2
  17.     D_b=np.mean(square(b))-E_b**2
  19.     σ_a=np.sqrt(D_a)
  20.     σ_b=np.sqrt(D_b)
  22.     corr_factor = cov_ab / (σ_a*σ_b)
  23.     return corr_factor
  25. r_ab=calc_corr(x1,x2)
  26. r_ac=calc_corr(x1,x3)
  27. r_bc=calc_corr(x2,x3)
  28. r_ab_c=(r_ab-r_ac*r_bc)/(((1-r_ac**2)**0.5)*((1-r_bc**2)**0.5))
  29. print('ab_c的一阶偏相关系数为：',r_ab_c)

image.png