ICCV 2019 论文标题:DeepGCNs: Can GCNs Go as Deep as CNNs? 论文地址:https://arxiv.org/abs/1904.03751 代码地址:https://sites.google.com/view/deep-gcns

简介
CNN在视觉任务上取得的成功很大程度归功于网络的深度,但擅长处理非欧式空间数据的GCN却受限于训练过程中梯度消失和过渡平滑等问题,而无法成功训练出足够深的GCN网络。本文借鉴ResNet、DenseNet以及Dilated Convolution的思想,将其运用在GCN中,成功构建了深度达到56层的GCN网络。最后,作者在点云语义分割任务中测试了深度GCN的有效性。本文的主要贡献在于讨论了深度GCN的有效性并提供了一种深度GCN的设计思路,这种深度GCN在更多的视觉任务中都有很大的应用潜力。
Representation Learning on Graphs
作者首先介绍了GCN的一般形式,严格来讲应该算是GNN的范畴了,但这部分将其数学形式归纳的很不错,就再记录一下吧。GCN的一般形式归纳为下式: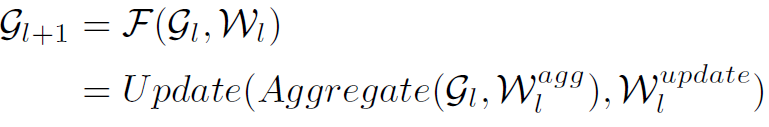
式中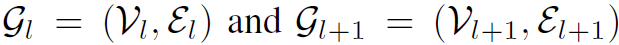 分别是第l层和第l+1层的graph。GCN的操作过程分为两步:aggregate和update,也就是式中的两个函数,参数分别是
分别是第l层和第l+1层的graph。GCN的操作过程分为两步:aggregate和update,也就是式中的两个函数,参数分别是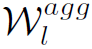 和
和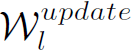 。aggregate函数的作用是将某个结点和其相邻结点的特征进行聚合,update函数的作用是根据聚合的特征对该结点的特征进行更新。常见的aggregate函数有mean aggregator、max-pooling aggregator、LSTM aggregator等。常见的update函数有MLP、GRU模型等。经典GCN的aggregate函数可以理解为mean aggregator,而update函数是MLP+Relu。
。aggregate函数的作用是将某个结点和其相邻结点的特征进行聚合,update函数的作用是根据聚合的特征对该结点的特征进行更新。常见的aggregate函数有mean aggregator、max-pooling aggregator、LSTM aggregator等。常见的update函数有MLP、GRU模型等。经典GCN的aggregate函数可以理解为mean aggregator,而update函数是MLP+Relu。
以结点形式表示GCN的一般形式如下: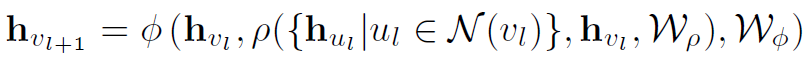
其中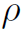 表示aggregate函数,
表示aggregate函数,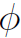 表示update函数,
表示update函数,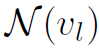 表示第l层结点v的邻接结点(可以是k阶邻接)。
表示第l层结点v的邻接结点(可以是k阶邻接)。
Residual Learning for GCNs
残差学习是训练深度CNN的关键,因此要训练深度GCN,肯定首先尝试将GCN与Residual Learning结合。作者给出了以下结合方式: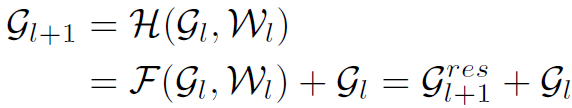
式子很好理解,就是在graph的每个结点层面上添加shortcut。这样一来,GCN学习的不再是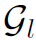 到
到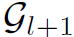 的映射,而是
的映射,而是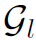 到
到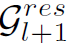 的映射,这是Residual Learning的核心思想。
的映射,这是Residual Learning的核心思想。
Dense Connections in GCNs
除了Residual Learning,DenseNet中的dense connectivity思想也是很好的训练深度网络的方式。作者同样将其与GCN结合: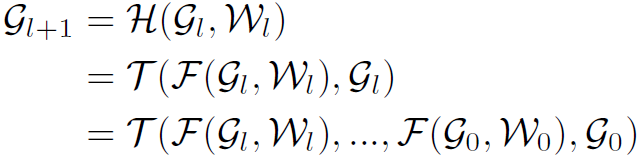
式中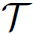 表示vertex-wise concatenation,也就是说层数越深,结点特征的维度越高。假设第0层结点特征维度为
表示vertex-wise concatenation,也就是说层数越深,结点特征的维度越高。假设第0层结点特征维度为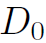 ,GCN每次输出的维度为
,GCN每次输出的维度为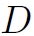 ,那么第l层结点特征的维度就达到了
,那么第l层结点特征的维度就达到了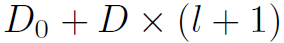 。
。
Dilated Aggregation in GCNs
Dilated Convolution可以在不进行pooling的情况下扩大卷积的感受野,作者也将这种思想引入了GCN中。要进行Dilated Aggregation首先要对结点的邻接结点进行排序,这里作者使用结点特征之间的L2距离衡量结点顺序。例如对于结点v,其有序邻接结点为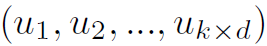 ,若以d为步长选择其邻接结点,则:
,若以d为步长选择其邻接结点,则: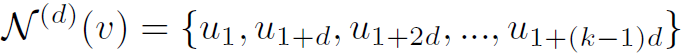
这些被筛选出来的邻接结点参与aggregate函数的聚合。上述过程如图3: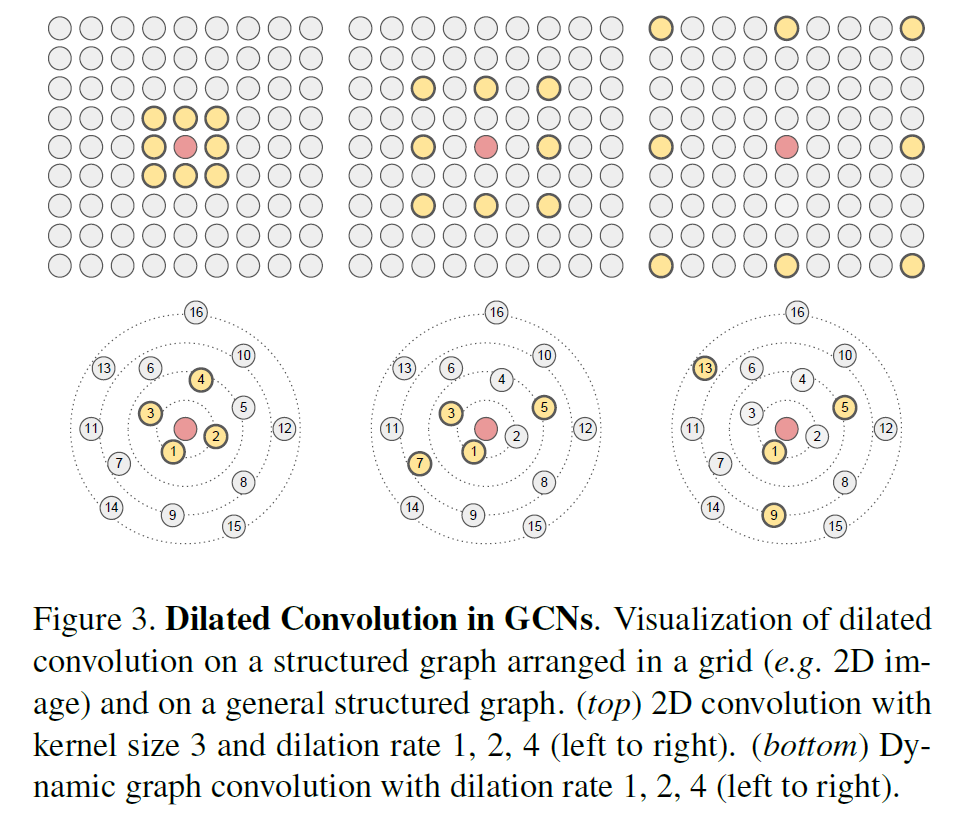
为了加强网络的泛化能力,作者还提出了一种随机采样的Dilated Aggregation方式用于网络的训练过程。
Network Architectures
以上就是作者构建深度GCN的模型基础。针对特定的点云分割任务,作者用上述模组分别构建了三种深度GCN: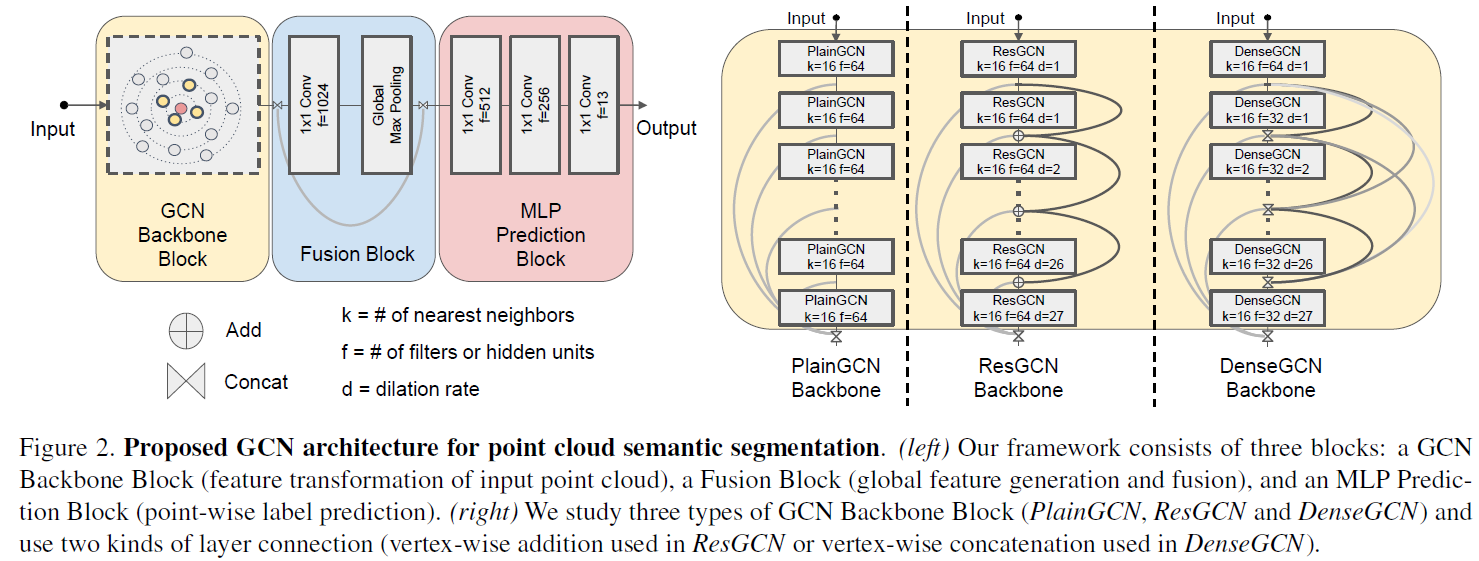
Results
表1展示了各种组件与深度对GCN模型表现的作用,可以看到ResGCN相对来讲表现最好,并且层数更多的GCN往往表现更好。表中#filters的含义我还不是很理解,有待以后在代码中查看细节。
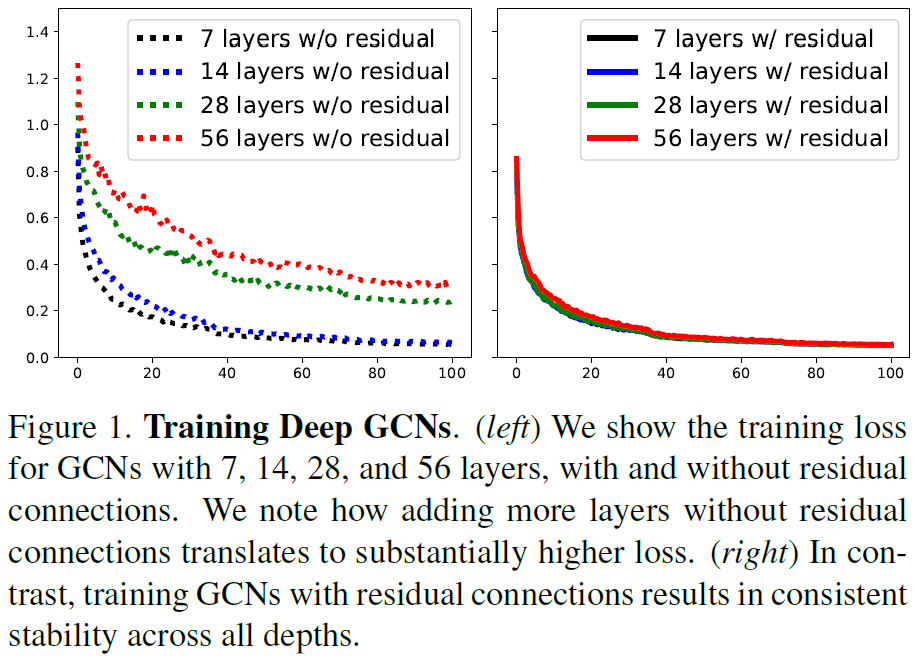
图1中可以看到,ResGCN可以在训练过程中表现出更好的稳定性,有效解决梯度消失和过渡平滑的问题。
图4和表2可以看到,深度GCN在实际应用中的表现也很好。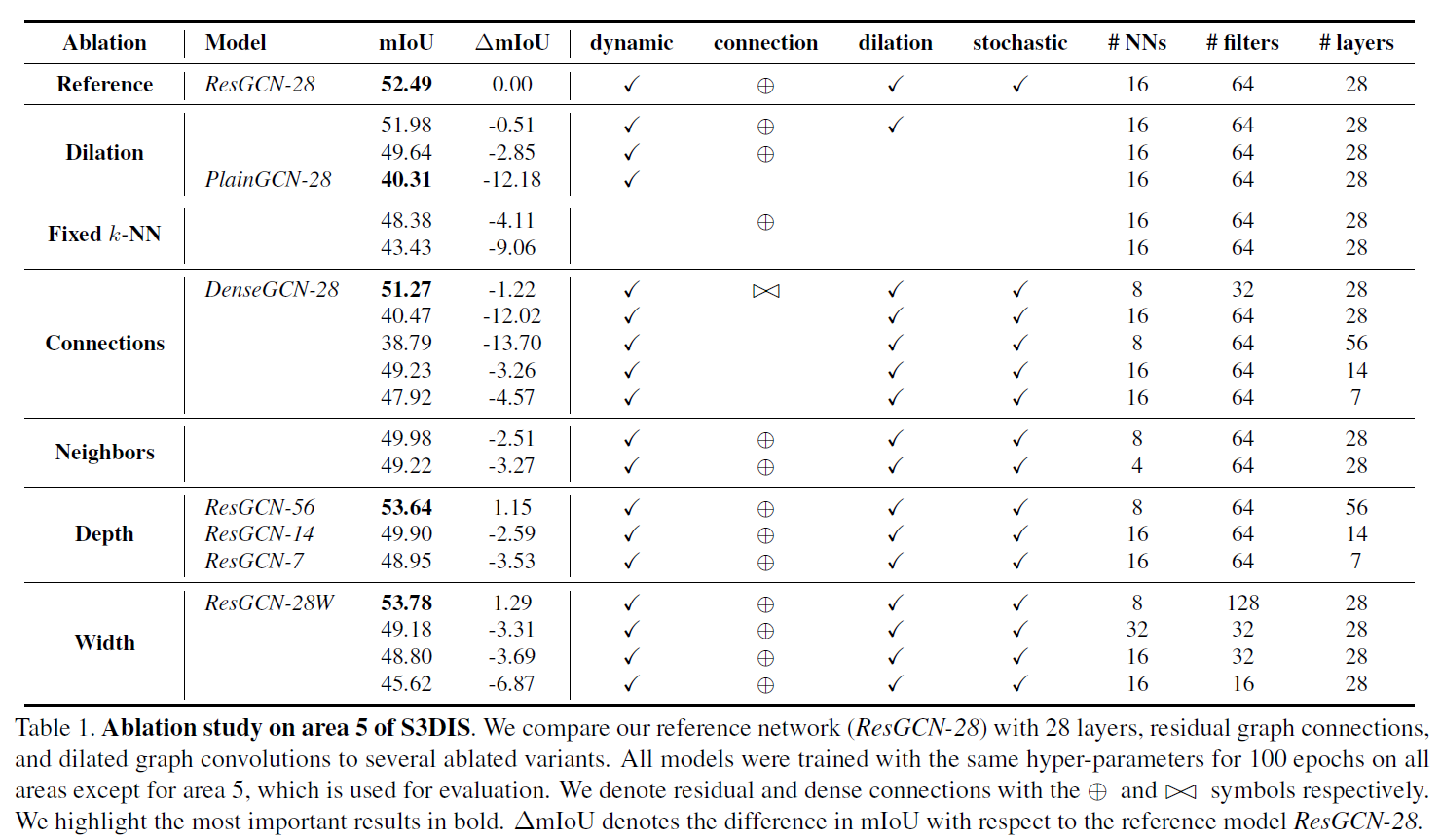

总结
挖坑的文章往往比填坑的文章更有意义。本文应该算是一个小小的挖坑文章吧,期待深度GCN在更多领域的表现。但目前来看,由于大多数RGB视觉任务中graph的规模都很小,深度GCN的应用场景还有待挖掘。

