1.1 自动控制系统概述1.1.1 自动控制的一般概念

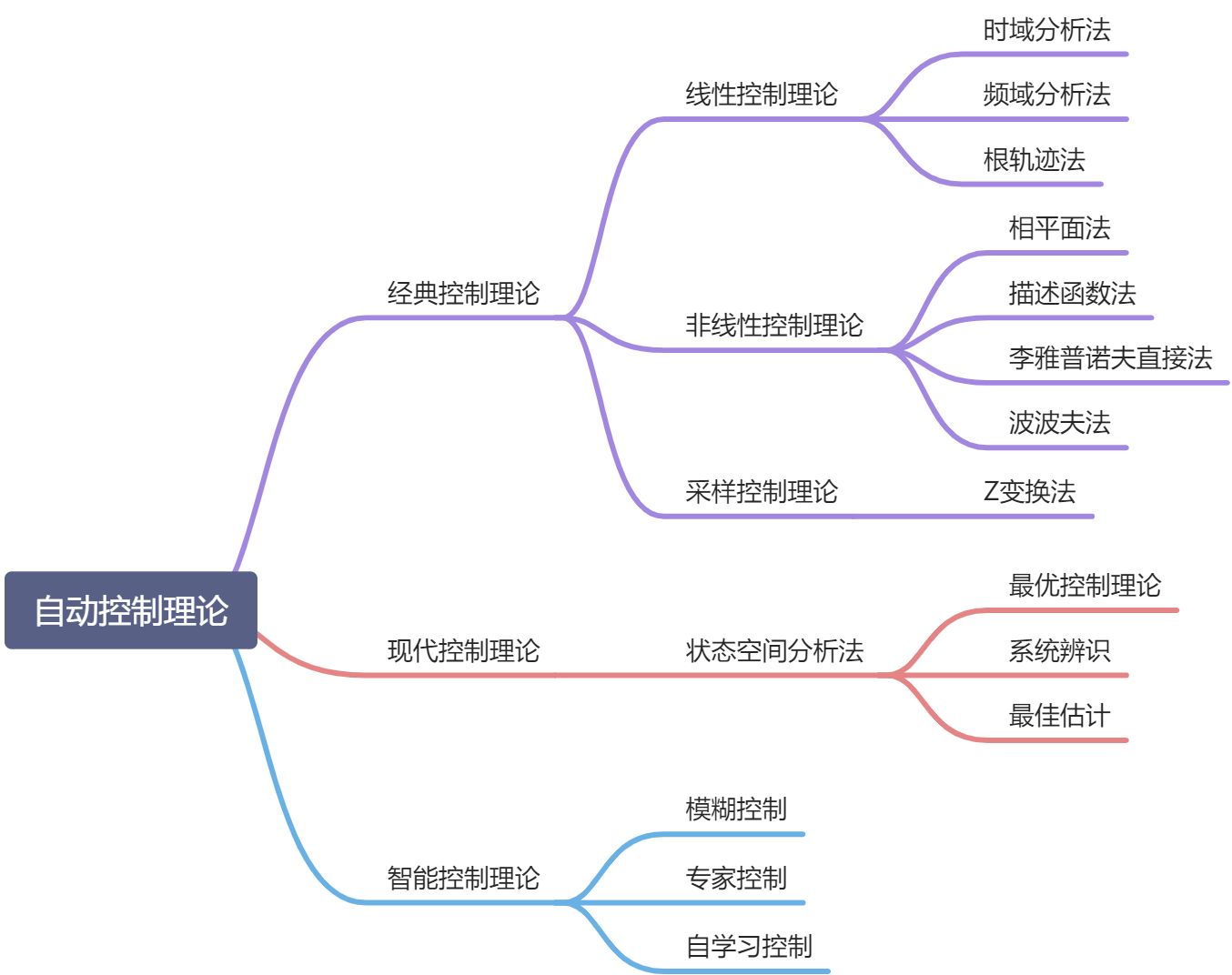
1.1.1 自动控制的一般概念

控制的含义

控制（CONTROL）——某个主体使某个客体按照一定的目的动作。
主体–人：人工控制； 机器：自动控制
客体–指一件物体，一套装置，一个物化过程，一个特定系统。

人工控制与自动控制

人在控制过程中起三个作用：
（1）观测：用眼睛去观测，如温度计、转速表等的指示值；
（2）比较与决策：人脑把观测得到的数据与要求的数据相比较，并进行判断，根据给定的控制规律给出控制量；
（3）执行：根据控制量用手具体调节，如调节阀门开度、改变触点位置。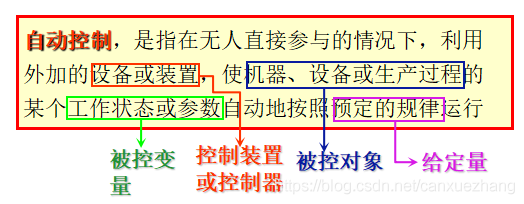

1.1.2 自动控制技术的发展

• 网上资料：自动控制技术发展史

1.1.3 自动控制系统组成

为了实现各种复杂的控制任务，首先要将被控对象和控制装置按照一定的方式连接起来，组成一个有机总体，这就是自动控制系统。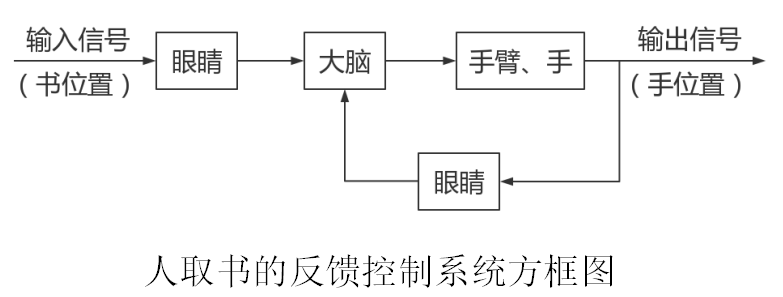


测量元件：其职能是检测被控制的物理量，如果这个物理量是非电量，一般要再转换为电量。例如，测速发电机用于检测电动机轴的速度并转换为电压；电位器、旋转变压器或自整角机用于检测角度并转换为电压；热电偶用于检测温度并转换为电压等。
给定元件：其职能是给出与期望的被控量相对应的系统输入量（即参据量）。
比较元件：其职能是把测量元件检测的被控量实际值与给定元件给出的参据量进行比较，求出它们之间的偏差。常用的比较元件有差动放大器、机械差动装置、电桥电路等。
放大元件：其职能是将比较元件给出的偏差信号进行放大，用来推动执行元件去控制被控对象。电压偏差信号可用集成电路、晶闸管等组成的电压放大级和功率放大级加以放大。
执行元件：其职能是直接推动被控对象，使其被控量发生变化。用来作为执行元件的有阀、电动机、液压马达等。
校正元件：也叫补偿元件，它是结构或参数便于调整的元部件，用串联或反馈的方式连接在系统中，以改善系统的性能。最简单的校正元件是由电阻、电容组成的无源或有源网络，复杂的则用电子计算机。
自动控制系统的组成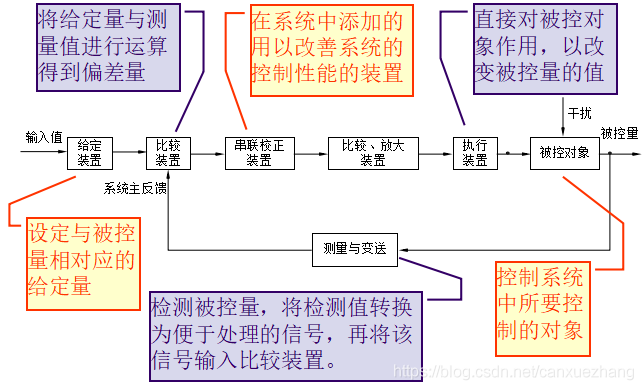

1.1.4 自动控制系统基本控制方式

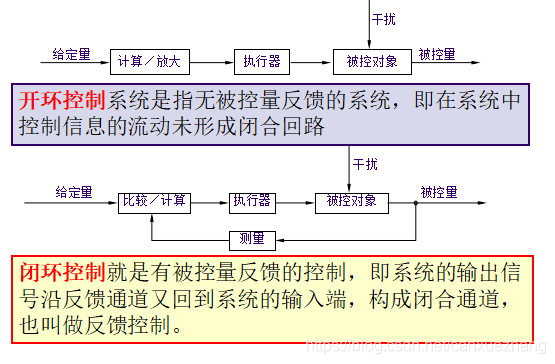
开环控制和闭环控制

典型开环系统

典型闭环系统

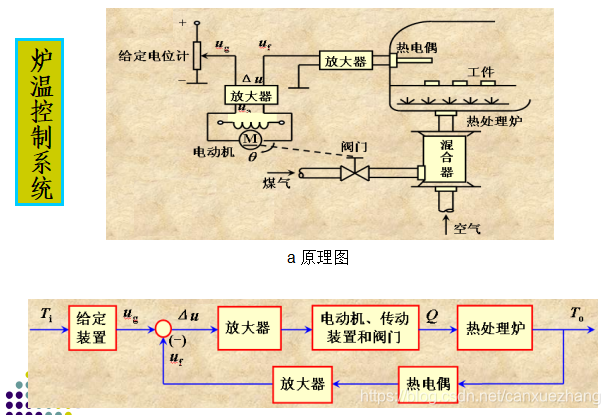
1.1.5 自动控制系统的分类

自动控制系统可以从不同的角度来进行分类，常见的有以下几种。
1.按输入量变化的规律分类
自动控制系统按输入量变化的规律可分为以下三类。
（1）恒值控制系统
恒值控制系统的特点系统的输入量是衡量，并且要求系统的输出量相应地保持恒定。恒值控制系统是最常见的一类自动控制系统，如自动调速系统、恒温控制系统、恒力控制系统等。
（2）随动控制系统
随动控制系统又称伺服控制系统，其特点是：输入量是随机变化着的，并且要求系统的输出量能跟随输入量的变化而作出相应的变化。随动控制系统在工业和国防上有着极为广泛的应用，例如机床刀架跟随系统、火炮跟踪控制系统、雷达导引系统和机器人控制系统等等。
（3）程序控制系统
程序控制系统的特点是：输入量按照一定的时间函数变化，并且要求输出量随之变化。例如数控伺服系统以及一些自动化生产线等。
2.按系统传输信号对时间的关系分类
自动控制系统按系统传输信号对时间的关系可分为两类。
（1）连续控制系统
连续控制系统的特点是：各元件的输入量与输出量都是连续量（模拟量），因此它又称为模拟控制系统。恒温控制系统就是连续控制系统。连续控制系统的运动规律通常可用微分方程来描述。
（2）离散控制系统
离散控制系统又称采样数据控制系统。它的特点是系统中有的信号是脉冲序列，或采样数据量、数字量。通常，采用数字计算机控制的系统都是离散控制系统。离散控制系统的运动规律通常可用差分方程来描述。
3.按系统的输出量和输入量间的关系分类
自动控制系统按系统的输出量和输入量间的关系可分为两类。
（1）线性系统
线性系统的特点是：系统全部由线性元件组成，它的输出量与输入量间的关系用线性微分方程来描述。线性系统最重要的特性，是可以应用叠加原理。
叠加原理：两个不同的作用量，同时作用于系统时的响应，等于两个作用量单独作用时响应的叠加。
（2）非线性系统
非线性系统的特点是：系统中存在有非线性元件，如具有死区、出现饱和、含有库仑摩擦等非线性特性的元件，它的输出量与输入量的关系要用非线性微分方程来描述。非线性系统不能应用叠加原理。
4.按系统中的参数对时间的变化情况分类
自动控制系统按系统中的参数对时间的变化情况可分为两类。
（1）定常系统
定常系统特点是：系统的全部参数不随时间变化，它的输出量与输入量间的关系用定常微分方程来描述。在实践中遇到的系统大多属于（或基本属于）这一类系统。
（2）时变系统
时变系统的特点是：系统中有的参数是时间t的函数，它随时间变化而改变。宇宙飞船控制系统就是时变控制系统的一个例子，宇宙飞船飞行过程中，飞船内燃料质量、飞船受的重力时刻都在发生变化。
当然，除了以上的分类方法外，还可以根据其他的条件对自动控制系统进行分类。本书根据课程教学大纲的要求，只讨论线性定常系统。

1.1.6 自动控制系统的任务

自动控制理论是研究自动控制共同规律的一门学科。尽管自动控制系统有不同的类型，对每个系统也都有不同的特殊要求，但对于各类系统来说，在已知系统的结构和参数时，我们感兴趣的都是系统在某种典型输入信号下，其被控量变化的全过程。例如，对恒值控制系统是研究扰动作用引起被控量变化的全过程；对随动系统是研究被控量如何克服扰动影响并跟随参据量的变化全过程。但是，对每一类系统被控量变化全过程提出的共同基本要求都是一样的，且可以归结为稳定性、快速性和准确性，即稳、准、快的要求。
1.稳定性
稳定性是保证控制系统正常工作的先决条件。一个稳定的控制系统，其被控量偏离期望值的初始偏差应随时间的增长逐渐减小并趋于零。具体来说，对于稳定的恒值控制系统，被控量因扰动而偏离期望值后，经过一个过渡过程时间，被控量应恢复到原来的期望值状态；对于稳定的随动系统，被控量应能始终跟踪参据量的变化。反之，不稳定的控制系统，其被控量偏离期望值的初始偏差将随时间的增长而发散，因此，不稳定的控制系统无法实现预定的控制任务。
线性自动控制系统的稳定性是由系统结构所决定的，与外界因素无关。这是因为控制系统中一般含有储能元件或惯性元件，如绕组的电感、电枢转动惯量、电炉热容量、物体质量等，储能元件的能量不可能突变，因此，当系统受到扰动或有输入量时，控制过程不会立即完成，而是有一定的延缓，这就使得被控量恢复期望值或跟踪参据量有一个时间过程，称为过渡过程。例如，在反馈控制系统中，由于被控对象的惯性，会使控制动作不能瞬时纠正被控量的偏差；控制装置的惯性使偏差信号不能及时完全转化为控制动作。这样，在控制过程中，当被控量已经回到期望值而使偏差为零时，执行机构本应立即停止工作，但由于控制装置的惯性，控制动作仍继续向原来方向进行，致使被控量超过期望值又产生符号相反的偏差，导致执行机构向相反方向动作，以减小这个新的偏差；另一方面，当控制动作已经到位时，又由于被控对象的惯性，偏差并未减小为零，因而执行机构继续向原来方向运动，使被控量又产生符号相反的偏差；如此反复进行，致使被控量在期望值附近来回摆动，过渡过程呈现振荡形式。如果这个振荡过程是逐渐减弱的，系统最后可以达到平衡状态，控制目的得以实现，我们称为稳定系统；反之，如果振荡过程逐步增强，系统被控量将失控，则称为不稳定系统。
2.快速性
为了很好完成控制任务，控制系统仅仅满足稳定性要求是不够的，还必须对其过渡过程的形式和快慢提出要求，一般称为动态性能。例如，对于稳定的高射炮射角随动系统，虽然炮身最终能跟踪目标，但如果目标变动迅速，而炮身跟踪目标所需过渡过程时间过长，就不可能击中目标；对用于稳定的自动驾驶仪系统，当飞机受阵风扰动而偏离预定航线时，具有自动使飞机恢复预定航线的能力，但在恢复过程中，如果机身摇晃幅度过大，或恢复速度过快，就会使乘员感到不适；函数记录仪记录输入电压时，如果记录笔移动很慢或摆动幅度过大，不仅使记录曲线失真，而且还会损坏记录笔，或使电器元件承受过电压。因此，对控制系统过渡过程的时间（即快速性）和最大振荡幅度（即超调量）一般都有具体要求。
3.准确性
理想情况下，当过渡过程结束后，被控量达到的稳态值（即平衡状态）应与期望值一致。但实际上，由于系统结构，外作用形式以及摩擦、间隙等非线性因素的影响，被控量的稳态值与期望值之间会有误差存在，称为稳态误差。稳态误差是衡量控制系统控制精度的重要标志，在技术指标中一般都有具体要求。

若有收获，就点个赞吧