题目

运用你所掌握的数据结构，设计和实现一个 LRU (最近最少使用) 缓存机制。它应该支持以下操作： 获取数据 get 和 写入数据 put 。

获取数据 get(key) - 如果密钥 (key) 存在于缓存中，则获取密钥的值（总是正数），否则返回 -1。

写入数据 put(key, value) - 如果密钥不存在，则写入其数据值。当缓存容量达到上限时，它应该在写入新数据之前删除最近最少使用的数据值，从而为新的数据值留出空间。

进阶:
你是否可以在 O(1) 时间复杂度内完成这两种操作？

示例:

  1. LRUCache cache = new LRUCache( 2 /* 缓存容量 */ );
  2. cache.put(1, 1);
  3. cache.put(2, 2);
  4. cache.get(1);       // 返回  1
  5. cache.put(3, 3);    // 该操作会使得密钥 2 作废
  6. cache.get(2);       // 返回 -1 (未找到)
  7. cache.put(4, 4);    // 该操作会使得密钥 1 作废
  8. cache.get(1);       // 返回 -1 (未找到)
  9. cache.get(3);       // 返回  3
  10. cache.get(4);       // 返回  4

来源：力扣（LeetCode）链接：https://leetcode-cn.com/problems/lru-cache

解析

LRU (最近最少使用) 缓存机制: Least Recently Used的缩写，即最近最少使用,选择最近最久未使用的页面予以淘汰。该算法赋予每个页面一个访问字段，用来记录一个页面自上次被访问以来所经历的时间 t，当须淘汰一个页面时，选择现有页面中其 t 值最大的，即最近最少使用的页面予以淘汰。

根据算法特点，第一快速，使用哈希；第二页面最久没被使用，表示数据要按照时间有序，使用链表结构。两者兼顾的数据结构—哈希链表。

方法1：Java的LinkHashMap实现LRU

  1. class LRUCache extends LinkedHashMap<Integer, Integer>{
  2.     private int capacity;
  4.     public LRUCache(int capacity) {
  5.         super(capacity, 0.75F, true);
  6.         this.capacity = capacity;
  7.     }
  9.     public int get(int key) {
  10.         return super.getOrDefault(key, -1);
  11.     }
  13.     public void put(int key, int value) {
  14.         super.put(key, value);
  15.     }
  17.     @Override
  18.     protected boolean removeEldestEntry(Map.Entry<Integer, Integer> eldest) {
  19.         return size() > capacity; 
  20.     }
  21. }
  23. /**
  24.  * LRUCache 对象会以如下语句构造和调用:
  25.  * LRUCache obj = new LRUCache(capacity);
  26.  * int param_1 = obj.get(key);
  27.  * obj.put(key,value);
  28.  */

复杂度分析
时间复杂度：对于 put 和 get 操作复杂度是 O(1)，因为有序字典中的所有操作： get/in/set/move_to_end/popitem（get/containsKey/put/remove） 都可以在常数时间内完成。
空间复杂度：O(capacity)，因为空间只用于有序字典存储最多 capacity + 1 个元素。

方法2：哈希表+双向链表

这个问题可以用哈希表，辅以双向链表记录键值对的信息。所以可以在 O(1) 时间内完成 put 和 get 操作，同时也支持 O(1) 删除第一个添加的节点。

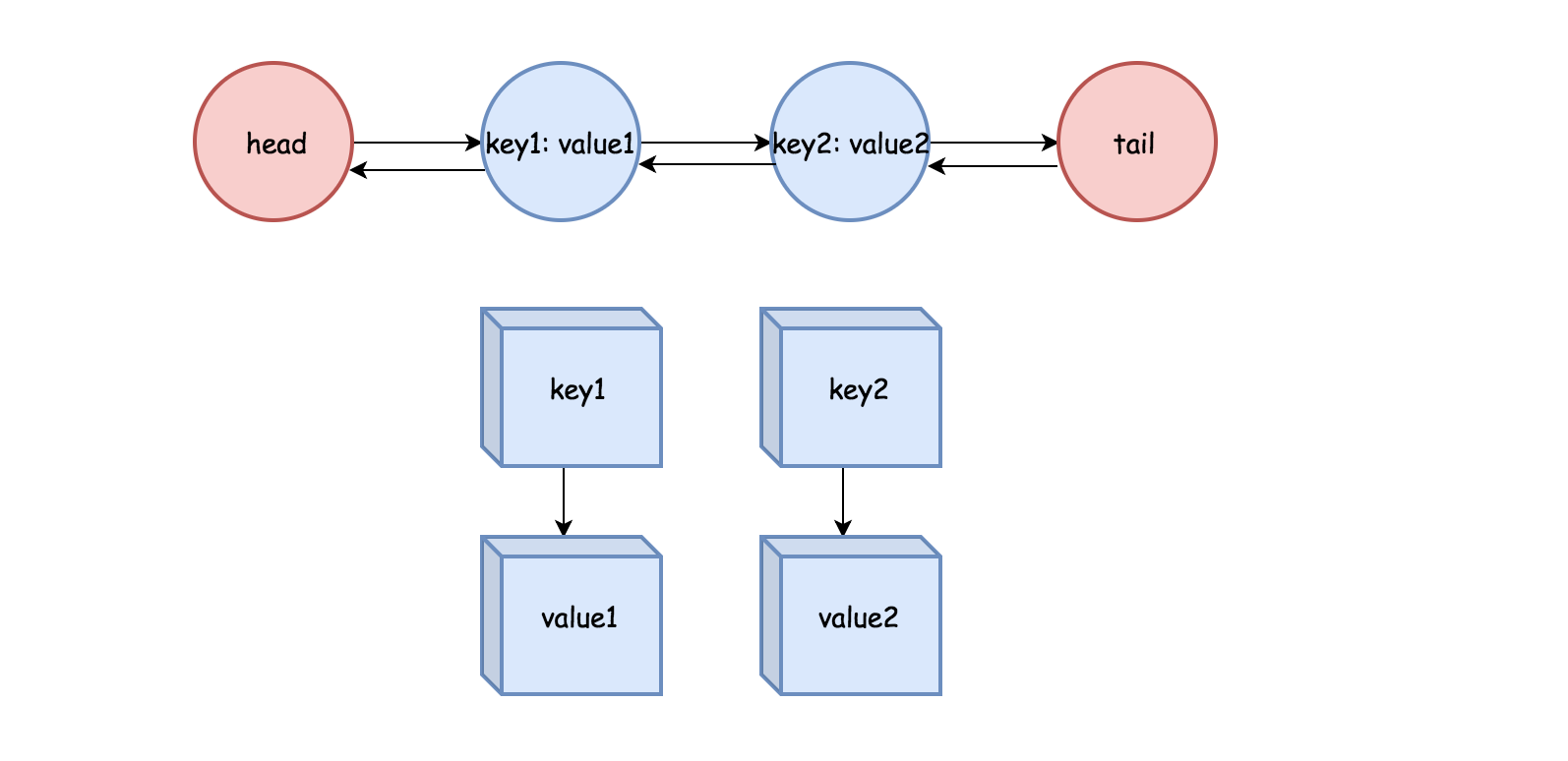
最近最少使用缓存机制 - 图1
为什么使用双向链表？
使用双向链表的一个好处是不需要额外信息删除一个节点，同时可以在常数时间内从头部或尾部插入删除节点。
一个需要注意的是，在双向链表实现中，这里使用一个伪头部和伪尾部标记界限，这样在更新的时候就不需要检查是否是 null 节点。

  1. import java.util.Hashtable;
  2. public class LRUCache {
  4.   class DLinkedNode {
  5.     int key;
  6.     int value;
  7.     DLinkedNode prev;
  8.     DLinkedNode next;
  9.   }
  11.   private void addNode(DLinkedNode node) {
  12.     /**
  13.      * Always add the new node right after head.
  14.      */
  15.     node.prev = head;
  16.     node.next = head.next;
  18.     head.next.prev = node;
  19.     head.next = node;
  20.   }
  22.   private void removeNode(DLinkedNode node){
  23.     /**
  24.      * Remove an existing node from the linked list.
  25.      */
  26.     DLinkedNode prev = node.prev;
  27.     DLinkedNode next = node.next;
  29.     prev.next = next;
  30.     next.prev = prev;
  31.   }
  33.   private void moveToHead(DLinkedNode node){
  34.     /**
  35.      * Move certain node in between to the head.
  36.      */
  37.     removeNode(node);
  38.     addNode(node);
  39.   }
  41.   private DLinkedNode popTail() {
  42.     /**
  43.      * Pop the current tail.
  44.      */
  45.     DLinkedNode res = tail.prev;
  46.     removeNode(res);
  47.     return res;
  48.   }
  50.   private Hashtable<Integer, DLinkedNode> cache =
  51.           new Hashtable<Integer, DLinkedNode>();
  52.   private int size;
  53.   private int capacity;
  54.   private DLinkedNode head, tail;
  56.   public LRUCache(int capacity) {
  57.     this.size = 0;
  58.     this.capacity = capacity;
  60.     head = new DLinkedNode();
  61.     // head.prev = null;
  63.     tail = new DLinkedNode();
  64.     // tail.next = null;
  66.     head.next = tail;
  67.     tail.prev = head;
  68.   }
  70.   public int get(int key) {
  71.     DLinkedNode node = cache.get(key);
  72.     if (node == null) return -1;
  74.     // move the accessed node to the head;
  75.     moveToHead(node);
  77.     return node.value;
  78.   }
  80.   public void put(int key, int value) {
  81.     DLinkedNode node = cache.get(key);
  83.     if(node == null) {
  84.       DLinkedNode newNode = new DLinkedNode();
  85.       newNode.key = key;
  86.       newNode.value = value;
  88.       cache.put(key, newNode);
  89.       addNode(newNode);
  91.       ++size;
  93.       if(size > capacity) {
  94.         // pop the tail
  95.         DLinkedNode tail = popTail();
  96.         cache.remove(tail.key);
  97.         --size;
  98.       }
  99.     } else {
  100.       // update the value.
  101.       node.value = value;
  102.       moveToHead(node);
  103.     }
  104.   }
  105. }
  107. /**
  108.  * LRUCache 对象会以如下语句构造和调用:
  109.  * LRUCache obj = new LRUCache(capacity);
  110.  * int param_1 = obj.get(key);
  111.  * obj.put(key,value);
  112.  */

复杂度分析
时间复杂度：对于 put 和 get 都是O(1)。
空间复杂度：O(capacity)，因为哈希表和双向链表最多存储 capacity + 1 个元素。

总结

学习使用哈希表和链表，明确双向链表的适用场景。