书籍推荐：数据挖掘导论(机械工业出版社)，机器学习(周志华)， 统计学习方法（李航）

决策树

是一种非参数的有监督学习方法，他能从一系列有特征和标签的数据中总结出决策规则，并用树状图的结构来呈现这些规则，以解决分类和回归问题。

决策树组成

根节点 —— 没有进边，只有出边。第一个节点。
中间节点 (内部节点)—— 既有进边也有出边。
叶子节点 —— 有进边没有出边，每一个叶子节点都是一个类别标签。
深度（depth）—— 有几层节点
子节点和父节点 —— 更接近根节点的是父节点

决策树的测评

数据集上的所有特征都可以拿来分枝，所以可以组合成很多种决策树，需要找到一颗全局最优树。可以使用“贪心策略”来达到次最优的决策树。也就是通过局部分枝最优化。

sklearn决策树(CART)

  1. import numpy as np
  2. import matplotlib.pyplot as plt
  3. from sklearn.datasets import load_iris
  4. from sklearn.tree import DecisionTreeClassifier
  6. iris = load_iris()
  7. X = iris.data[:, 2:]
  8. y = iris.target
  10. plt.scatter(X[y == 0,0], X[y == 0,1])
  11. plt.scatter(X[y == 1,0], X[y == 1,1])
  12. plt.scatter(X[y == 2,0], X[y == 2,1])
  13. plt.show()
  15. dt_clf = DecisionTreeClassifier(max_depth=2, criterion="entropy")
  16. dt_clf.fit(X,y)

我们应该在每个节点的用哪个维度做划分，维度上的哪个值上划分？
首先介绍信息熵，它是用来度量随机变量的不确定度，商越大，数据的不确定性越高，商越小，数据的不确定性越低。
Decision Tree - 图2
上述公式中P代表标记出现的概率。为什么要在公式前面加负号，因为P出现表示的概率必然是小于1的。对小于一的数求log，必然小于0，所以加负号。log以2为底计算出的信息熵，单位是比特，e是奈特，3是铁特，python的log不指定默认以e为底。

如何更直观的理解信息熵公式？
我们假设一组数据集中样本，只有两种标记（服从伯努利分布）。则上述公式可以转化为。
Decision Tree - 图3 x表示标记1出现的概率，（x-1）是标记二出现的概率。

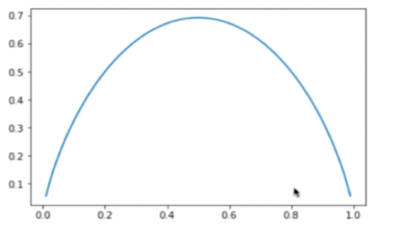
二分类信息熵模拟

  1. import numpy as np
  2. import matplotlib.pyplot as plt
  4. def entropy(p):
  5.     return -p * np.log(p) - (1-p) * np.log(1-p)
  7. x = np.linspace(0.01, 0.99, 300)
  8. plt.plot(x, entropy(x))
  9. plt.show()

image.png

当其中一种分类出现的概率x = 0.5的时候，信息熵最大，不确定性最大。

决策树自实现

  1. from collections import Counter
  2. from math import log
  3. import numpy as np
  5. def split(X, y, d, value):
  6.     index_a = (X[:,d]) <= value)
  7.     index_b = (X[:,d] > value)
  8.     return X[index_a], X[index_b], y[index_a], y[index_b]
  11. def entropy(y):
  12.     counter = Counter(y)
  13.     res = 0.0  # res = 1
  14.     for num in counter.values():
  15.         p = num / len(y)
  16.         res += -p * log(p)  # res -= p**2
  18. def try_split(X, y):
  20.     best_entropy = float('inf')
  21.     best_d,best_v = -1,-1
  22.     for d in range(X.shape[1]):
  23.         sorted_index = np.argsort(X[:,d])
  24.         for i in range(1, len(X)):
  25.             if X[sorted_index[i-1],d] != X[sorted_index[i], d]:
  26.                 v = (X[sorted_index[i-1],d] + X[sorted_index[i], d]) / 2
  27.                 X_1,X_r,y_1,y_r = split(X,y,d,v)
  29.     return best_entropy,best_v,best_d

基尼系数

Decision Tree - 图5
衡量数据不确定性的另一种指标，相较于信息熵，不用进行Decision Tree - 图6计算，可以提高计算效率。sklearn默认使用基尼系数（criterion = ‘jini’）

ID3

决策树的缺点

决策边界横平竖直，不一定可以进行非常好的划分，比如不能斜着切
对个别数据敏感，非参数模型都这样，删掉或加入一个样本本点，可能切分结果就会不一样

超参数

depth：深度
random_state：score会在某个值附近波动，导致画出来的每一棵树都不一样。但是当我们引入random_state参数，代码如下所示，最后得到的决策树就会一致。
criterion：划分依据，criterion = ‘jini’、’entropy’