三角函数

https://www.bilibili.com/video/BV1G7411A72i?p=3

任意角
平面内一条射线绕其端点从一个位置旋转到另一个位置所形成的图形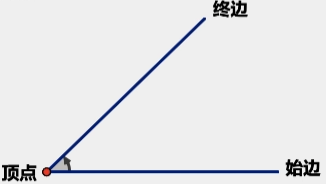

角的三要素
顶点、始边、终边

角的三种分类

1. 锐角：、直角：、钝角：、周角：、平角
2. 任意角：
   1. 正角：射线绕其端点逆时针旋转形成的角
   2. 负角：按顺时针方向旋转形成的角
   3. 零角：射线没有做任何旋转
3. 象限角和轴线角
   1. 象限角：
      1. 角的顶点在原点
      2. 始边与x轴正半轴重合
      3. 终边落在第几象限此角就是第几象限角
   2. 轴线角
      1. 终边落在坐标轴上的角

小练习

1. 锐角是第_象限角。 # 一
2. -215°是第__象限角。 # 二

3. 画出-180°角和1070°角。 #

   终边相同的角

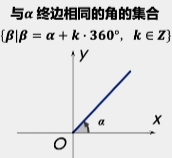
   所有与角终边相同的角，连同角在内，可以构成一个集合：
   
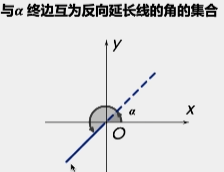
   所有与终边互为反向延长线的角的集合
   
   
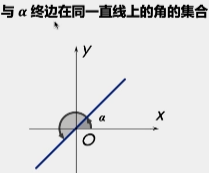
   与终边在同一条直线上的角的集合
   ：推理过程是将上述两个集合描述法变成 k180°
   
   终边与终边垂直的角的集合
   
   
   与终边关于x轴对称的角的集合
   
   
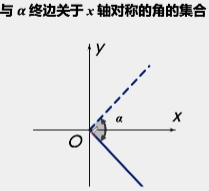
   与终边关于y轴对称的集合
   
   
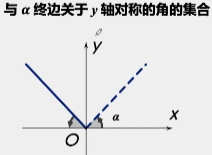
   *略：练习—终边相同的角 p3

   轴线角集合与象限角集合

   轴线角集合

4. 终边落在 x 轴 正半轴 上的所有角的集合。

5. 终边落在 y 轴 正半轴 上的所有角的集合。

1. 终边落在 x 轴 负半轴 上的所有角的集合。

1. 终边落在 y 轴 负半轴 上的所有角的集合。

1. 终边落在x轴正半轴上的所有角的集合。

1. 终边落在x轴正半轴上的所有角的集合。

1. 终边落在x轴正半轴上的所有角的集合。

象限角集合

1. 第一象限角的集合

1. 第二象限角的集合

1. 第三象限角的集合

1. 第四象限角的集合

略：练习—轴线角与象限角 p5

角度制与弧度制的换算

角度制

把圆周 360 等分，其中一份所对的圆心角就是1°

弧度制

长度等于 半径长 的圆弧所对的圆心角叫做1弧度（1 rad）的角。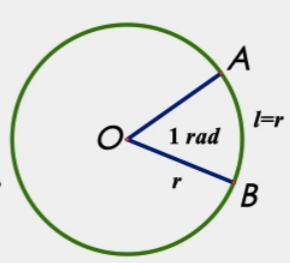

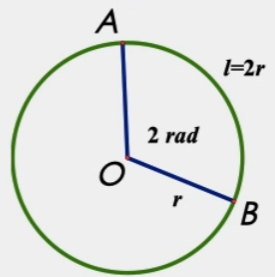
弧度计算公式：（l为弧度长，r为半径）
角度与弧度的互换关系：
圆的周长 l 的计算公式，当n=360°时，化简为。
将n=360, 180代入弧度计算公式，。
通常我们省略尾部的rad，

注意

• 正角的弧度制是一个正数，负角的弧度制时一个负数，零角的弧度制是0.
• 角的弧度数的绝对值（l为弧度长，r为半径）
• 用角度制和弧度制来度量零角，单位不同，但数量相同（都是0）；用角度制和弧度制来度量任一非零角，单位不同，度量也不同。
• 在同一式子中角度、弧度不可以混用

  常用弧度数

  
  

  弧长公式和扇形面积

  弧长公式

  初中：，高中：

  扇形面积公式

  初中：，高中：
  略：练习—弧长公式和扇形面积

  任意角的三角函数定义

  初中复习：对于一个直角三角形，

设是一个任意角，，它的终边与单位圆（半径为单位长度：1）交于点p（x，y）
正弦 ：y 叫做 的正弦函数，记作，即，
余弦 ：x 叫做 的正弦函数，记作，即，
正切 ： 叫做 的正弦函数，记作，即，
总结 ：正弦、余弦、正切都是以 角 为自变量，以单位圆上的点的 坐标或坐标的比值 为函数值的函数，将它们统称为三角函数。

正弦余弦正切值在各象限的符号

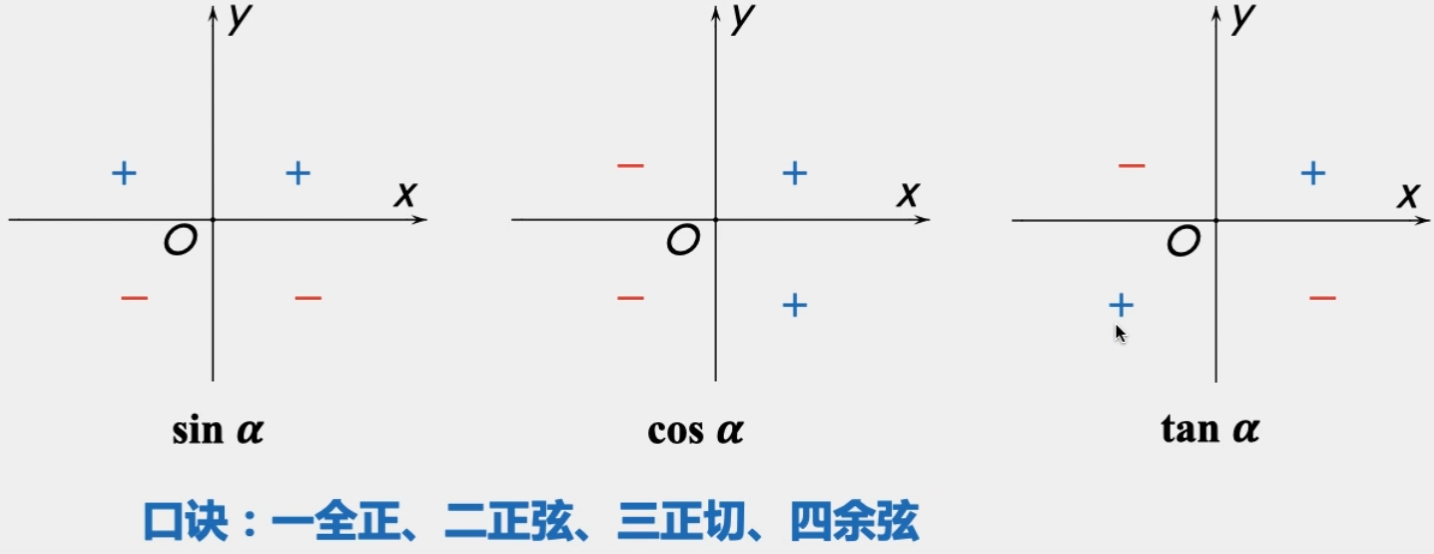
暂停p15