特征选择

我们将样本的属性称之为特征，对当前学习任务有用的特征称之为相关特征，无用的称之为无关特征。从给定的特征集合中选取相关特征子集的过程，称之为特征选择。与之相反的有个叫做特征扩增的东西。
特征选择可以减少冗余和噪音，提高计算效率，但是可能会降低模型的预测能力。

过滤法（Filter）

按照发散性或相关性对各个特征，进行评分，设定阈值或者待选择阈值的个数，选择特征

去掉取值变化小的特征（Removing features with low variance）

也叫 方差选择法 这是通过特征本身的方差来筛选特征的类。比如一个特征本身的方差很小，就表示样本在这个特征上基本没有差异，可能特征中的大多数值都一样，甚至整个特征的取值都相同，那这个特征对于样本区分没有什么作用。所以无论接下来的特征工程要做什么，都要优先消除方差为0的特征。VarianceThreshold有重要参数threshold，表示方差的阈值，表示舍弃所有方差小于threshold的特征，不填默认为0，即删除所有的记录都相同的特征。

import numpy as np
from sklearn.datasets import load_boston
from sklearn.feature_selection import VarianceThreshold
boston = load_boston()
X = boston.data
y = boston.target
filter = VarianceThreshold(threshold=0.2)  # 默认为0,此处表示方差小于0.2的特征列将被剔除
new_X = filter.fit_transform(X)
print(filter.variance_)
print(X.shape[1])
print(new_X.shape[1])

伯努利分布是假设随机变量x取值要么为0，要么为1，取1发生的概率为p，那么取0的概率是1-p

单变量特征选择 (Univariate feature selection)

对于分类问题 可采用：

卡方检验

只能用于二分类，经典的卡方检验是检验定性自变量对定性因变量的相关性。假设自变量有 N 种取值，因变量有 M 种取值，考虑自变量等于 i 且因变量等于 j 的样本频数的观察值与期望的差距，构建统计量：
https://zhuanlan.zhihu.com/p/69888032（简易版）
统计学之卡方检验（原文出处）

Ai为实际出现的频次，T_i为理论出现的频次。卡方检验就是用来反应理论频数和实际频数差异的大小，差异越大，卡方值越大，差异越小，卡方值越小。怎么评判卡方值的大小？引入卡方分布并以及查表。
print(model.score)

from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
from sklearn.datasets import load_iris
#导入IRIS数据集
iris = load_iris()
model1 = SelectKBest(chi2, k=2)#选择k个最佳特征
model1.fit_transform(iris.data, iris.target)
print(model1.score_,pvalues_)  # 输出p值和得分

对于回归问题可采用：

相关系数法

• 皮尔森相关系数

只能处理俩个特征的线性关系，倾向于1的时候是正相关倾向于-1的时候是负相关倾向于0的时候是没有线性关系。
正相关的时候要删除，举例税收和收入高度正相关，说明收入可以由税收倒推，该列可删除。当特征列与标签列正相关的时候则相反，正相关则说明该特征对结果的正面影响相应较大。

https://www.zhihu.com/question/26235175/answer/761828836 # 协方差是啥
https://www.zhihu.com/question/20099757 # 样本方差为毛要除以n-1

要理解Pearson相关系数，首先要理解协方差（Covariance），协方差是一个反映两个随机变量相关程度的指标，如果一个变量跟随着另一个变量同时变大或者变小，那么这两个变量的协方差就是正值，反之相反，公式如下：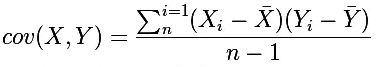

Pearson相关系数公式如下：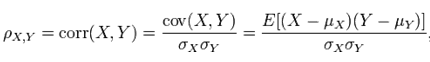

由公式可知，Pearson相关系数是用协方差除以两个变量的标准差得到的，虽然协方差能反映两个随机变量的相关程度（协方差大于0的时候表示两者正相关，小于0的时候表示两者负相关），但是协方差值的大小并不能很好地度量两个随机变量的关联程度，例如，现在二维空间中分布着一些数据，我们想知道数据点坐标X轴和Y轴的相关程度，如果X与Y的相关程度较小但是数据分布的比较离散，这样会导致求出的协方差值较大，用这个值来度量相关程度是不合理的，如下图：

为了更好的度量两个随机变量的相关程度，引入了Pearson相关系数，其在协方差的基础上除以了两个随机变量的标准差，容易得出，pearson是一个介于-1和1之间的值，当两个变量的线性关系增强时，相关系数趋于1或-1；当一个变量增大，另一个变量也增大时，表明它们之间是正相关的，相关系数大于0；如果一个变量增大，另一个变量却减小，表明它们之间是负相关的，相关系数小于0；如果相关系数等于0，表明它们之间不存在线性相关关系。《数据挖掘导论》给出了一个很好的图来说明：

import pandas as pd
from sklearn.datasets import load_iris
iris = load_iris()
data = iris.data
target = iris.target
df = pd.DataFrame(data=data, columns=target)
metric = df.corr(method='pearson') # spearman

结合热力图绘制相关系数

import seaborn as sns
import matplotlib.pyplot as plt
sns.heatmap(metric, annot=True，cmap='Blues')  # annot,绘图的同时标记数字
plt.show()

• 斯皮尔曼相关系数

• 肯德尔相关系数

  互信息( mutual_info_classif/regression) - 捕捉每个特征与标签之间的任意关系

  互信息法 返回”每个特征与目标之间的互信息量的估计”，估计量∈[0, 1]
  0 - 两个变量独立
  1 - 两个变量完全相关
  互信息系数能够很好地度量各种相关性，但是计算相对复杂一些，互信息计算公式如下：

%20%3D%5Csum%20%7B%20x%5Cin%20X%20%7D%7B%20%5Csum%20%7B%20y%5Cin%20Y%20%7D%7B%20P%5Cleft(%20x%2Cy%20%5Cright)%20log%5Cfrac%20%7B%20P%5Cleft(%20x%2Cy%20%5Cright)%20%20%7D%7B%20P%5Cleft(%20x%20%5Cright)%20P%5Cleft(%20Y%20%5Cright)%20%20%7D%20%20%7D%20%20%7D%20%0A#card=math&code=I%5Cleft%28%20X%3BY%20%5Cright%29%20%3D%5Csum%20%7B%20x%5Cin%20X%20%7D%7B%20%5Csum%20%7B%20y%5Cin%20Y%20%7D%7B%20P%5Cleft%28%20x%2Cy%20%5Cright%29%20log%5Cfrac%20%7B%20P%5Cleft%28%20x%2Cy%20%5Cright%29%20%20%7D%7B%20P%5Cleft%28%20x%20%5Cright%29%20P%5Cleft%28%20Y%20%5Cright%29%20%20%7D%20%20%7D%20%20%7D%20%0A&height=41&id=uAESO)

使用 feature_selection 库的 SelectKBest 类结合最大信息系数法来选择特征的代码如下

#互信息法
#互信息系数能够很好地度量各种相关性，但是计算相对复杂一些，互信息计算公式如下：
#使用 feature_selection 库的 SelectKBest 类结合最大信息系数法来选择特征的代码如下
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import mutual_info_classif
#选择K个最好的特征，返回选择特征后的数据
SelectKBest(mutual_info_classif, k=2).fit_transform(iris.data, iris.target)

基于独立假设
这种方法比较简单，易于运行，易于理解，通常对于理解数据有较好的效果（但对特征优化、提高泛化能力来说不一定有效）。这种方法有许多改进的版本、变种。单变量特征选择基于单变量的统计测试来选择最佳特征。它可以看作预测模型的一项预处理。

包装法（Wrapper）

递归消除法

只支持逻辑回归和数型算法

嵌入法（Embedding）

套索回归