线性回归中只能处理线性关系，处理非线性关系的数据时可以使用多元线性回归。

把变成，也就是用一元线性回归的式子处理非线性的问题。也就是所谓的升维（增加特征列，但图像还是二维）。

调包使用

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
x = np.random.uniform(-3,3,size=100)
X = x.reshape(-1, 1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0,1,size=100)   # 生成正态分布的数据集，正太分布指的是大部分数据落在一块区间
''' # 添加多项式特征，最高为2次幂'''
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(degree=2)  # 添加多项式特征，最高为2次幂
poly.fit(X)
X2 = poly.transform(X)
X2.shape  # 第一列是x的0次方，第二列是原列，第三列是二次方列
'''out: (100, 3)'''
'''建立模型并用模型的参数预测标签'''
lin_reg = LinearRegression()
lin_reg.fit(X2, y)
y_predict2 = lin_reg.predict(X2)
'''绘制源数据散点图和预测标签曲线图'''
plt.scatter(x, y)
plt.plot(np.sort(x),y_predict2[np.argsort(x)],color='r')
plt.show()

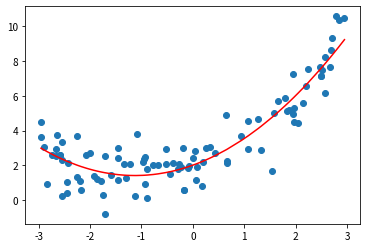
'''输出系数和截距'''
print(lin_reg.coef_)
print(lin_reg.intercept_)

pipline使用多项式回归

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
poly_reg = Pipeline({
    ("poly",PolynomialFeatures(degree=2)),
    ("std_scaler", StandardScaler()),  # 归一化是为了让梯度下降时效率更高
    ("lin_reg", LinearRegression())
})
poly_reg.fit(X,y)
y_predict = poly_reg.predict(X)