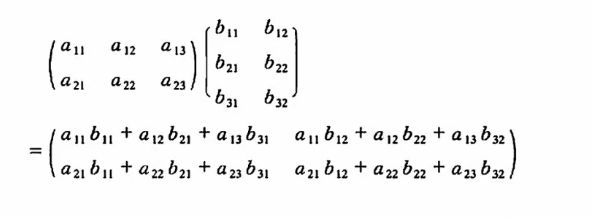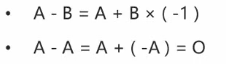什么是矩阵

  • 矩阵（Matrix）是一个按照长方阵列排列的复数或实数集合
  • 矩阵最早来自于方程组的系数及常数所构成的方阵，最初是用来解决线性方程求解的工具
  • 矩阵是高等代数中常见的工具，也常见于统计分析等应用数学学科中；矩阵在物理学和计算机科学中都有应用

  • 矩阵的运算是数值分析领域的重要问题

    矩阵的基本概念

  • 由m n个数a（i = 1,2,……m; j = 1, 2,……,n）排成的m行n列的数表A就称为m行n列的*矩阵

  • 这m n个数称作矩阵A的*元素，元素a位于矩阵A的第i行第j列
  • m * n 矩阵A可以记作A，其中m为行数，n为列数，m，n > 0
  • 对于A，如果m = n，即矩阵的行数与列数相等，那么称A为方阵，也可以叫n阶方阵，记作A
  • 只有一行的矩阵称为行向量，只有一列矩阵的称为竖向量
  • 对于方阵，从左上角到右下角的直线，叫做主对角线，主对角线上的元素称为主对角线元素
  • 矩阵的元素全部为0，称为零矩阵，用O表示
  • 对于方阵，如果只有对角线元素为1，其余元素都为0，那么称为单位矩阵，一般用 I 或者E表示

  • 对于方阵，不在对角线上的元素都为0，称为对角矩阵

    矩阵的加法

  • 把矩阵的对应位元素相加

  • 矩阵的形状必须一致，即必须是同型矩阵

    矩阵的乘法

    数与矩阵相乘

    • 数值与矩阵每一个元素相乘

      矩阵与矩阵相乘

    • 左矩阵的每一行与右矩阵的每一列，对应每一个元素相乘；A B，那么有A矩阵m n，B矩阵n k，要求左侧矩阵的列数n，必须等于右侧矩阵的行数n，结果矩阵C为m k

    • 乘法规则：一行乘一列，行定列移动，列尽下一行

      image.png

      矩阵的转置

  • 行列转换(行变列，列变行)

image.png

  • 把矩阵A的行换成同样序数的列，得到一个新矩阵，叫做A的转置矩阵，记作A
  • 当A为m n 矩阵时，转置后为n m矩阵

矩阵的运算法则

加法

  • A + B = B + A
  • (A + B) + C = A + (B + C)

乘法
image.png
减法
image.png
转置
image.png
这块没看，p5 30分左右

矩阵的逆

image.png

  • 除以一个矩阵等价于乘以一个矩阵的逆