引用书籍：高等数学（上下册）（李忠）数学分析（第1，2，3册）（伍胜建）数学分析中的典型问题与方法（第二版）（裴礼文）简明线性代数（丘维声）最优化理论与方法（袁亚湘）（Stephen Boyed and Lieven Vandenberghe.Convex optimization。Cam university press，2009）BBC数学的故事（纪录片）数学大师 从芝诺到庞加莱（徐源译），天才引导的历程（苗锋译）：：数学历史读物演示网站和软件：Wolfram AlphaMatlabPython
集合以及集合的概念
- 集合：“一堆东西”放在一起，称为 集合 (set)，通常用大写字母表示，A
- 元素：“一堆东西”里面的一个称之为 元素 (element)，通常用小写字母表示，a
- a属于A
； a不属于A 
。
- a属于A
- 描述方式:列举和描述
- 列举法：A= {1, 2, 3}
- 描述法：B= {x : x是有理数} # 前边是变量名，后面是描述。冒号是集合建构式符号，冒号和竖线是一样的，意思是“使得（such that，简写为s.t.）”
- 子集：A的每一个元素都在B中，记为
- 相等，记为A=B
- 真子集
且
，记为
- 空集
- 集合运算
- 交：
- 并：
- 补：
- 交：
- 任意
- 存在
- 基数：集合中元素的个数称为集合的基数（又称为势），记作
，例子：
。 - 常见的集合：自然数
，整数
，有理数
，实数
，复数
。 # 空心字母代表印刷体
实数集
- 区间
开区间与闭区间，
前开后闭与前闭后开
- 邻域
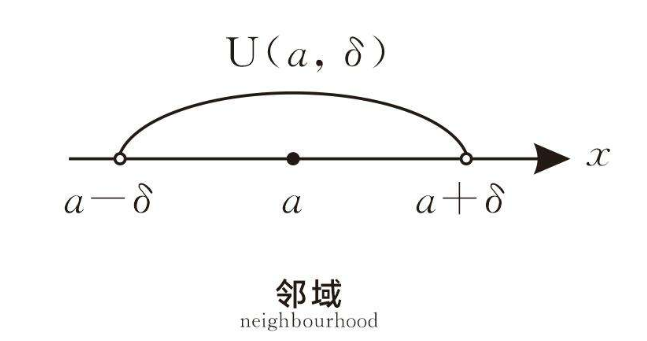
# 空心邻域，不包含a- 数轴
- 实数集上的数和数轴上的点一一对应
- 由直线，正方向，原点，单位长度组成
- 无理数和有理数在数轴上都以稠密
的状态存在。
比如a，b的定义域是[0,1]，列式子
表示a，b之间的有理数，则k的定义域是[0,10]，n的定义域是
。然后有理数加无理数还是无理数，所以无理数在数轴上也是稠密状态存在。
所以实数集在数轴上是连续的，那么怎么描述“连续性”？
- 完备性刻画- 在实数域中，任意一个单调有界序列必然有极限- 单调指的是单调递增或者单调递减- 有界指的是有最大值或者最小值- 确界存在定理- 上界：集合，并且，如果存在，使得对于，有，则称有上界，并且说是的一个上界。- 下界：同理，换成- 上确界：设是一个非空数集，如果满足- 是的一个上界- 对，存在使得，则称为的上确界，确界在有限域中必须取到，记为- 下确界：- 确界存在定理即：非空有上界的实数集必然有上确界，非空有下界的实数集必然有下确界
实数集的基数（势）怎么描述
三角不等式
，即两边之和大于等于第三边。
- 伯努利 （Bernoulli）不等式
- 对于任意的
和任意的正整数n，有
，假设n=2即可证明。
- 对于任意的
算术-几何平均值不等式
- 对于任意n个非负实数
有
- 左边代表的是算数均值，右边代表的是几何均值。
- 取等号的充要条件是所有元素相等时。
- 充分条件：p是条件，q是结论，p能推出q，p是q的充分条件 视频
- 必要条件：p是条件，q是结论，q能推出p，则p是q的必要条件。
映射
- 对于任意n个非负实数
映射：设A、B是两个非空集合，如果存在一个法则f，使得对A中的每个元素a，按法则f，在B中有唯一确定的元素b与之对应，则称f为从A到B的映射，记作：
。
到集合
存在双射，称
与
等势，记为
。特别的，称与自然数集
等势的集合为可列集
# 整数集被自然数集labelencode
# 使用二维坐标轴构造可列有理数
# 
在
对应的图像可以表示
，然后（0, 1）对应到
（康托定理）
其中，b 称为元素 a 在映射 f 下的象，记作
；a 称为 b 关于映射 f 的原象。也称 A 为原象集，B 为象集。
- 单射（嵌入映射） # 少的萝卜多的坑
- 双射（一一映射） # 一个萝卜一个坑
- 满射（到上映射） # 多的萝卜少的坑
函数
对于给定的集合
，如果存在一个对应法则 f，使得对于X中的每一个数x，在
中存在唯一的数 y 与之对应，则称对应法则 f 为从 X 到 R 的一个函数，记作：
ps是：是元素映射的话就要变成竖杠加箭头
其中 y 称为 f 在 x 的值，X 称为函数 f 的定义域，数集
称为函数 f 的值域，记作
；x 称为自变量，y 称为因变量
六类基本初等函数
- 常值函数
- 幂函数
- 指数函数
- 对数函数
- 指数函数的反函数（大学叫 逆函数 ），对数公式是数学中的一种常见公式，如果 a^x=N(a>0,且a≠1)，则 x 叫做以 a 为底 N 的对数,记做 x=log(a)(N)，其中 a 要写于 log 右下。其中 a 叫做对数的底，N 叫做真数 [1] 。通常我们将以 10 为底的对数叫做常用对数，以 e 为底的对数称为自然对数
- 三角函数
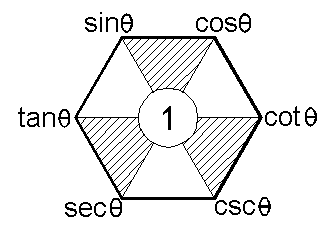
- 如上：三角函数六边形记忆法
- 三角形上边俩个数的平方等于下边那个数，例子：
- 在对角线上，俩个边上的点相乘等于中间的点，例子：
- 一个角上的数等于顺时针旋转后的俩个角上的数相除，例子：
- 三角形上边俩个数的平方等于下边那个数，例子：
反三角函数
四则运算
- 复合运算
- 反函数
- 如果 f 是双射，那么 f 可逆，记作
- 如果 f 是双射，那么 f 可逆，记作
基本初等函数经过有限次四则运算和复合所得到的函数称为初等函数。
几个特殊的函数
符号函数
ps：可视化见下图
- 高斯（Gauss）取整函数
- 当
时，有
，如下图 
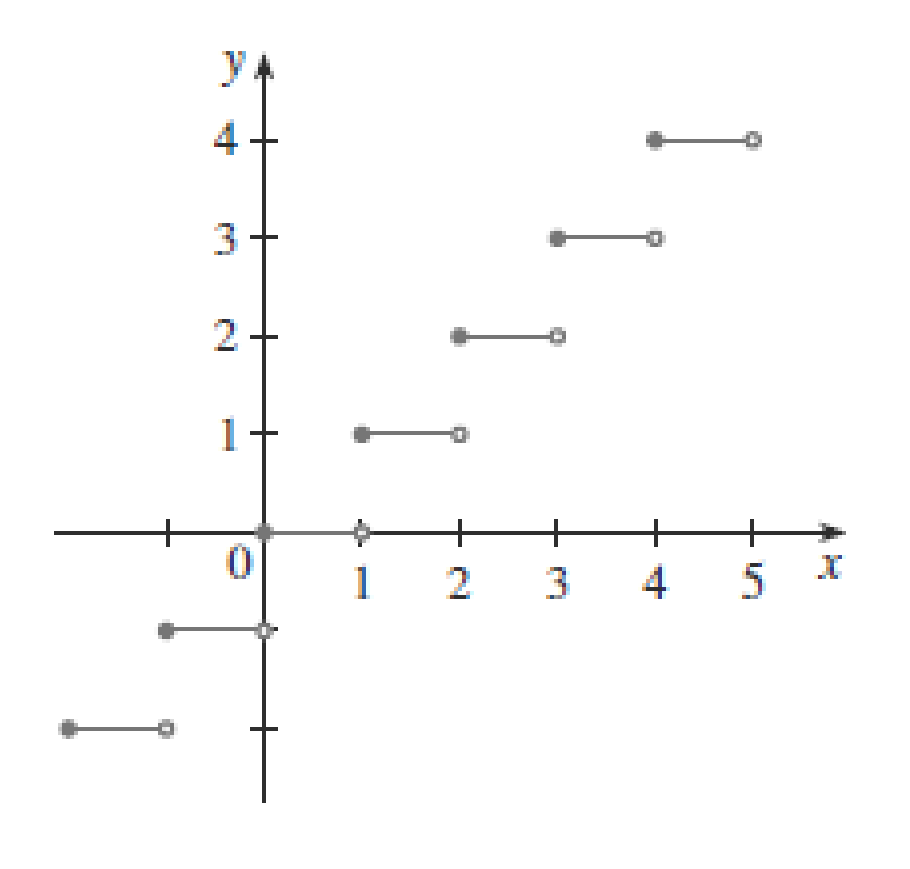
- 又叫阶梯函数，原因是长得像楼梯
- 当
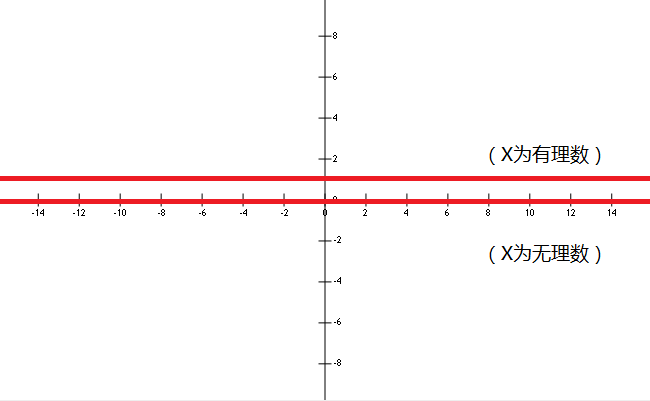
- 狄利克雷（Dirichlet）函数
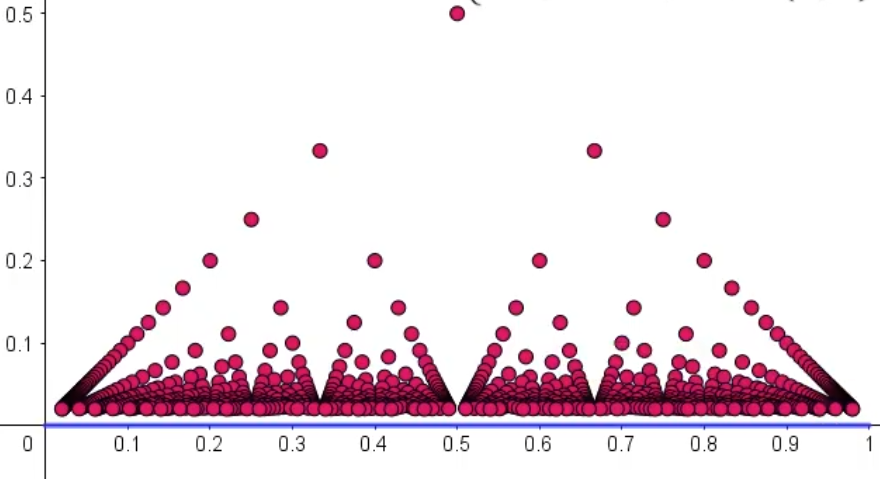
黎曼（Riemann）函数
有界性
- 存在常数M，使得对
，都有
，则称 
在 
有上界 - 存在常数M，使得对
，都有
，则称 
在 
有下界 
在 X 上有上界且有下界称
在 X 上有界- 例子：
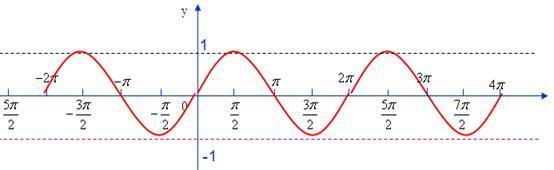
- sinx 有界
在正实数上有下界面，在负实数上有上界
- sinx 有界
- 存在常数M，使得对
- 单调性
- 对于任意
，只要
，就有
，称
在 X 上单调递增，如果把
换成
，则称严格单调递增。 - 例子： 等会写
- 对于任意
周期性
- 存在
，使得对于
，有
，则称 T 是是周期，
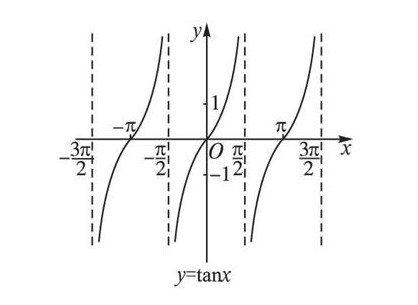
是以 T 为周期的函数。 - 例子：tanx
- 存在
奇偶性
- 描述的是函数关于 y 轴或者原点的对称性，所以 X 的定义域必须关于原点对称
- 奇函数
，例子：sinx，图像关于原点对称 - 偶函数
，例子：cosx，图像关于 y 轴对称 - 证明奇函数的反函数还是奇函数
- 等会写
定义在 
上
若有收获，就点个赞吧
0 人点赞
