序列 极限定义
- 序列实际上是从
到
的一个函数
- 也就是说自然数列中的每一个元素对应因变量。
- 但是我们也通常把序列看成按照一定顺序排列的数
例子:
举例三个序列
,画图可知当
,即 n 趋向于正无穷的时候,
趋向于0。
,画图可知当
,即 n 趋向于正无穷的时候,
趋向于0。
- 前者代表偶数项,后者代表奇数项。画图可知当
,即 n 趋向于正无穷的时候,
趋向于0。

- 前者代表偶数项,后者代表奇数项。画图可知当
由上述三个式子可知,当 n 在 趋于无穷 的时候,
可以 任意接近 一个数 l 。
- 那么应该如何描述“趋于无穷”和“任意接近”
- 由上引出极限的定义:设
是一个序列,如果存在常数 l ,使得
,有
: N的描述
- 则称该序列是收敛的,并且称 l 为该序列的极限(或者说序列收敛于 l ),记为
- 如果不存在这样的 l ,那么称
是发散序列。
- 上述描述语言叫做
语言
- 用该语言描述发散序列时只需要把任意和存在调换就可以。
- 则称该序列是收敛的,并且称 l 为该序列的极限(或者说序列收敛于 l ),记为
,
可以改写为
唯一性:收敛序列的极限是唯一的。
- 有界性:收敛序列是有界的。
- 保序性:
,存在
使得
,只要
,则
。
- 四则运算:设
,则
- 子序列收敛:
,则
的任意一个子序列
- 单调收敛原理:单调有界的实数序列一定会有极限。
序列极限性质的证明
略 。。。。。。。。。。。。。。。。。
序列极限的计算,略略略夹逼收敛原理
设序列,满足存在
使得
。
若,则
。
使用了保序性的原理。
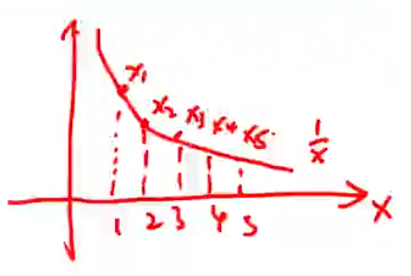
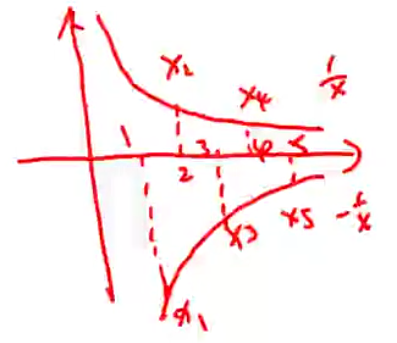
 图示,用邻域的角度阐述极限
图示,用邻域的角度阐述极限
