八种样本抽样方法介绍

介绍

你肯定很熟悉以下情况：你下载了一个比较大的数据集，并开始分析并建立你的机器学习模型。当加载数据集时，你的计算机会爆出”内存不足”错误。

即使是最优秀的人也会遇到这种事。这是我们在数据科学中面临的最大障碍之一，在受计算限制的计算机上处理大量数据(并非所有人都拥有Google的资源实力!)。

那么我们如何克服这个问题呢?是否有一种方法可以选择数据的子集并进行分析，并且该子集可以很好地表示整个数据集?

这种方法称为抽样。我相信你在学校期间，甚至在你的职业生涯中，都会遇到这个名词很多次。抽样是合成数据子集并进行分析的好方法。但是，那我们只是随机取一个子集呢?

我们将在本文中进行讨论。我们将讨论八种不同类型的抽样技术，以及每种方法的使用场景。这是一篇适合初学者的文章，会介绍一些统计的知识

什么是抽样?

让我们从正式定义什么是抽样开始。

抽样是一种方法，它使我们能够基于子集(样本)的统计信息来获取总体信息，而无需调查所有样本。

上图完美地说明了什么是抽样。让我们通过一个例子更直观的进行理解。

我们想要找到Delhi这个城市所有成年男性的平均身高。Delhi的人口大约为3千万，男性大约为1500万(这些都是假想数据，不要当成实际情况了)。你可以想象，要找到Delhi所有男性的身高来计算平均身高几乎是不可能的。
我们不可能接触到所有男性，因此我们无法真正分析整个人口。那么，什么可以我们做的呢?我们可以提取多个样本，并计算所选样本中个体的平均身高。

但是，接下来我们又提出了一个问题，我们如何取样?我们应该随机抽样吗?还是我们必须问专家?

假设我们去篮球场，以所有职业篮球运动员的平均身高作为样本。这将不是一个很好的样本，因为一般来说，篮球运动员的身高比普通男性高，这将使我们对普通男性的身高没有正确的估计。

这里有一个解决方案，我们在随机的情况下随机找一些人，这样我们的样本就不会因为身高的不同而产生偏差。

为什么我们需要抽样?

我确定你在这一点上已经有了直觉的答案。

抽样是为了从样本中得出关于群体的结论，它使我们能够通过直接观察群体的一部分(样本)来确定群体的特征。

选择一个样本比选择一个总体中的所有个体所需的时间更少
样本选择是一种经济有效的方法
对样本的分析比对整个群体的分析更方便、更实用

抽样步骤

将概念形象化是在记忆的好方法。因此，这是一个以流程图形式逐步进行抽样的流程图!

让我们以一个有趣的案例研究为例，将这些步骤应用于执行抽样。几个月前，我们在印度举行了大选。你一定看过当时每个新闻频道的民意调查:

这些结果是根据全国9亿选民的意见得出的还是根据这些选民的一小部分得出的?让我们看看是怎么做的。

第一步

抽样过程的第一步是明确定义目标群体。

因此，为了进行民意调查，投票机构仅考虑18岁以上且有资格在人口中投票的人。

第二步

抽样框架(Sampling Frame) –这是构成样本总体的个体列表。
因此，这个例子的抽样框架将是名字出现在一个选区的所有投票人列表。

第三步

一般来说，使用概率抽样方法是因为每一张选票都有相等的价值。不考虑种姓、社区或宗教，任何人都可以被包括在样本中。不同的样品取自全国各地不同的地区。

第四步

样本量(Sample Size) -是指样本中所包含的个体的数量，这些个体的数量需要足量以对期望的准确度和精度进行推断。

样本量越大，我们对总体的推断就越准确。

在民意调查中，各机构试图让尽可能多的不同背景的人参与抽样调查，因为这有助于预测一个政党可能赢得的席位数量。

第五步

一旦确定了目标人群，抽样框架，抽样技术和样本数量，下一步就是从样本中收集数据。

在民意测验中，机构通常会向人民提出问题，例如他们要投票给哪个政党或前政党做了什么工作，等等。

根据答案，各机构试图解释选民投票给谁，以及一个政党要赢得多少席位。

不同类型的抽样技术

这里是另一个图解!这一个是关于我们可以使用的不同类型的采样技术: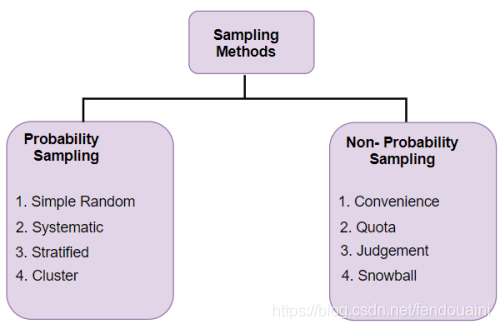

• 概率抽样（随机抽样）： 在概率抽样中，总体中的每个个体都有相等的被选中的机会。概率抽样给了我们最好的机会去创造一个真正代表总体的样本

• 非概率抽样（非随机抽样）：在非概率抽样中，所有元素被选中的机会都不相等。因此，有一个显著的风险，即最终得到一个不具代表性的样本，它不会产生可推广的结果。多用于质性研究：

  • 质性研究是以研究者本人作为研究工具，在自然情境下，采用多种资料收集方法（访谈、观察、实物分析），对研究现象进行深入的整体性探究，从原始资料中形成结论和理论，通过与研究对象互动，对其行为和意义建构获得解释性理解的一种活动。”

例如，假设我们的人口由20个人组成。每个个体的编号从1到20，并由特定的颜色(红色、蓝色、绿色或黄色)表示。在概率抽样中，每个人被选中的概率是1/20。

对于非概率抽样，这些概率是不相等的。一个人被选中的机会可能比别人大。现在我们对这两种抽样类型有了一定的了解，让我们分别深入了解每种抽样类型，并理解每种抽样的不同类型。

概率抽样的类型

简单随机抽样

这是你一定要遇到的一种抽样技术。在这里，每个人都是完全由随机选择的，人口中的每个成员都有被选择的机会。

简单的随机抽样可减少选择偏差。

这种技术的一大优点是它是最直接的概率抽样方法。但它有一个缺点，它可能不会选择特别多我们真正感兴趣的个体元素。蒙特卡罗方法采用重复随机抽样的方法对未知参数进行估计。

系统抽样

在这种类型的抽样中，第一个个体是随机选择的，其他个体是使用固定的“抽样间隔”选择的。让我们举一个简单的例子来理解这一点。

假设我们的总体大小是x，我们必须选择一个样本大小为n的样本，然后，我们要选择的下一个个体将是距离第一个个体的x/n个间隔。我们可以用同样的方法选择其余的。

假设，我们从第3个人开始，样本容量是5。因此，我们要选择的下一个个体将是(20/5)= 4，从第3个人开始，即7(3 4)，依此类推。
3、3 4=7、7 4=11、11 4=15、15 4=19 . 3、7、11、15、19
系统抽样比简单随机抽样更方便。然而，如果我们在人群中选择项目时存在一种潜在的模式，这也可能导致偏差(尽管这种情况发生的几率非常低)。

分层抽样

在这种类型的抽样中，我们根据不同的特征，如性别、类别等，把人口分成子组(称为层)。然后我们从这些子组中选择样本: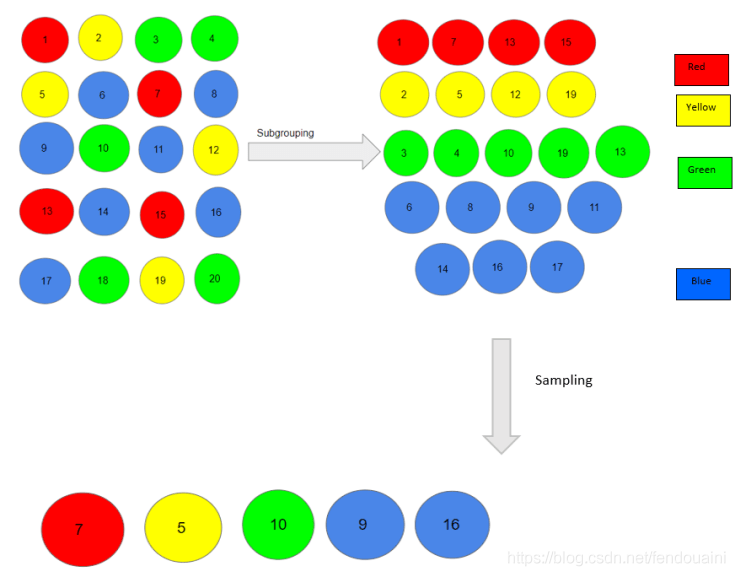

在这里，我们首先根据红、黄、绿、蓝等不同的颜色将我们的种群分成不同的子组。然后，从每一种颜色中，我们根据它们在人口中的比例选择一个个体。

当我们想要从总体的所有子组中得到表示时，我们使用这种类型的抽样。然而，分层抽样需要适当的人口特征的知识。

整群抽样

在整群抽样中，我们使用总体的子组作为抽样单位，而不是个体。全体样本被分为子组，称为群，并随机选择一个完整的群作为抽样样本。

在上面的例子中，我们将人口分为5个群。每个群由4个个体组成，我们在样本中选取了第4个群。我们可以根据样本大小包含更多的群。

当我们集中在一个特定领域或区域时，就会使用这种类型的抽样。

上述摘自 磐创AI csdn blog

非概率抽样的类型

1、任意抽样：也可以叫做便利抽样、方便抽样或者偶遇抽样，这个抽样方法是以便利为原则的，所以带有很大的偶然性和随意性。

任意抽样是所有抽样技术中花费最少经费和时间的，常见的街头随访或拦截式访问、邮寄式调查、杂志内问卷调查等都属于便利抽样的方式。这种方法能及时获得信息数据，省时省力，能为非正式的探索性研究提供很好的数据源。

但任意抽样容易产生显著的偏见，因为抽样可能不能代表诸如宗教或人口的性别等具体特征。同时，许多可能的选择偏差都会存在，如被调查者的自我选择、抽样的主观性偏差等。这种抽样不能直接代表总体和推断总体。
比如下图，假设编号为4、7、12、15和20的个体想要成为样本的一部分，因此，我们将把它们包含在样本中。

2、配额抽样：配额抽样是非随机抽样中最为普遍运用的一种方式。我们根据预先确定的总体特征来选择样本。跟随机抽样里的分层抽样类似，它也需要先将总体按照一定的特性分成不同类别，然后在每个类别里选取样本。

例如根据人口的性别、年龄构成来给调查员规定不同性别、年龄的调查人数（即配额）。配额保证了在这些特征上 样本的组成与总体 的组成是一致的。一旦配额分配好了，选择样本元素的自由度就很大了，唯一的要求就是所选的元素要适合所控制的特性。
这种抽样方法的目的是使样本对总体具有更好的代表性，但仍不一定能保证样本就是有代表性的。如果与问题相关联的某个特征未被考虑进配额，配额样本可能就不具有代表性，但在实施中包括太多的控制特征是十分困难的。
比如，考虑到我们必须为我们的样本选择一个倍数为4的个体，因此，编号为4、8、12、16和20的个人已经为我们的样本保留。

配额抽样和分层随机抽样既有相似之处，也有很大区别。配额抽样和分层随机抽样有相似的地方，都是事先对总体中所有单位按其属性、特征分类，这些属性、特征我们称之为“控制特性。”例如市场调查中消费者的性别、年龄、收入、职业、文化程度等等。然后，按各个控制特性，分配样本数额。但它与分层抽样又有区别，分层抽样是按随机原则在层内抽选样本，而配额抽样则是由调查人员在配额内主观判断选定样本（ 即必须拥有与研究问题相关联的特征 ）。

3、判断抽样：判断抽样是指基于调查人员的主观意愿、经验知识，依据对总体相关特征的了解，从目标总体中抽取有代表性的典型样本的做法，也称为选择性抽样。

比如，从全体企业中选择若干先进的、居中的、落后的企业作为样本，来考察全体企业经营状况。如果判断准确，这个方法可能取得代表性较好的样本，但这种方法受到主观因素的影响较大。适用于总体规模不大，样本量小，以及样本不易分门别类挑选的情况，较多用于探索性研究。
假设，我们的专家认为，应该将编号为1、7、10、15和19的人作为我们的样本，因为它们可以帮助我们更好地推断人口。你可以想象，配额抽样同样也容易受到专家的偏见，不一定具有代表性。

4、滚雪球抽样：这种方式，指的是以“滚雪球”似的方法，通过接触少量样本，再逐步通过这些少量样本获取大量样本。

它要求总体的样本之间有一定的关联性，才会产生这样滚雪球的可能。比如要做宝妈样本，调查人员先找到自己认识的几个宝妈，然后通过这些宝妈，继续寻找他们认识的宝妈。当抽样框架难以识别时，这种采样方法是有效的。
比如，我们随机选择了1个人作为样本，然后他推荐了6个人，6个人推荐了11个人，依此类推：

滚雪球抽样也有比较大的选择偏见风险，因为被引用的个体将与推荐他们的个体具有比较共同的特征。

上述摘自 调研工厂 知乎 blog https://www.bilibili.com/video/BV1KE411F7BK 视频参考