主成分分析法

• 一个非监督学习的算法
• 主要用于数据的降维
• 通过降维，可以发现更便于人类理解的特征
• 其他应用：可视化（ 多维变成2维）；去噪音(我们降维后丢失的信息可能很大一部分是噪音)

尽量使点与点之间距离最大，也就是最还原原来点与点之间状态距离
如何定义样本间的距离？使用方差，方差是用来描述样本整体分布疏密的指标，方差越大说明样本间越稀疏，越小说明越紧密，所以我们需要找一根线，样本点映射到这根线时，方差最大。

方差公式：

第一步，需要将样本的均值归零(demean)，也就是所有样本减去样本均值。

此时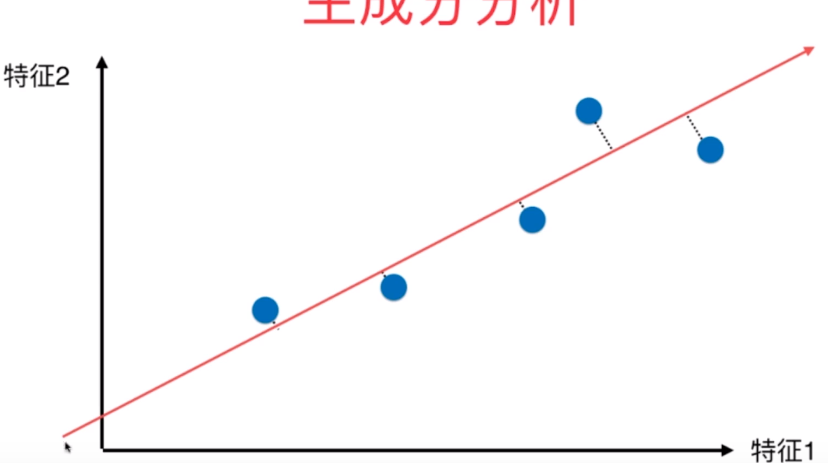因为均值归零，公式简化成图中所示

主成分分析法主要使用梯度上升法来（sklearn使用数学的方法），使得样本保留的方差（目标函数）最大。

p7.9 人脸识别，太困了，先不看了

sklearn使用PCA

import numpy as np
import matplotlib.pyplot as plt
from numpy.testing._private.utils import KnownFailureException
from sklearn import datasets
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.decomposition import PCA
digits = load_digits()
X = digits.data
y = digits.target
X_train, X_test, y_train,y_test = train_test_split(X, y, random_state=666)
print(X_train.shape)
'''使用原始数据分类并测试'''
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train, y_train)
print(knn_clf.score(X_test,y_test))  # out:0.98
'''降维到2维'''
pca = PCA(n_components=2)
pca.fit(X_train)
X_train_reduction = pca.transform(X_train)
X_test_reduction = pca.transform(X_test)
'''使用降维后的数据分类并测试'''
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train_reduction,y_train)
print(knn_clf.score(X_test_reduction, y_test))  # out:0.60
'''explained_variance_ratio_ 指标，会输出pac指定主成分个数后，每个主成分可以解释多少原数据的方差，\
（并从大到小排列），因为PCA寻找主成分就是找使得原来的数据方差维持的最大'''
pca.explained_variance_ratio_
pca = PCA(n_components=X_train.shape[1])  # 有多少列就输出多少主成分
pca.fit(X_train)
pca.explained_variance_ratio_  # 这样就可以看到每一个主成分可以解释的原来的数据的方差
'''绘制按大小排列的主成分代表的最大方差和与主成分数量的关系'''
plt.plot([i for i in range(X_train.shape[1])], 
        [np.sum(pca.explained_variance_ratio_[:i+1]) for i in range(X_train.shape[1])])  # 从0开始，所以要加1
plt.show()
'''保持解释原数据集95%方差'''
pca = PCA(0.95)
pca.fit(X_train)
pca.n_components_  # 输出pca后有多少维度数据
'''使用0.95 pca后的数据集测试分数'''
X_train_reduction = pca.transform(X_train)
X_test_reduction = pca.transform(X_test)
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train_reduction)
print(knn_clf.score(X_test_reduction, y_test))  # out: 0.9799