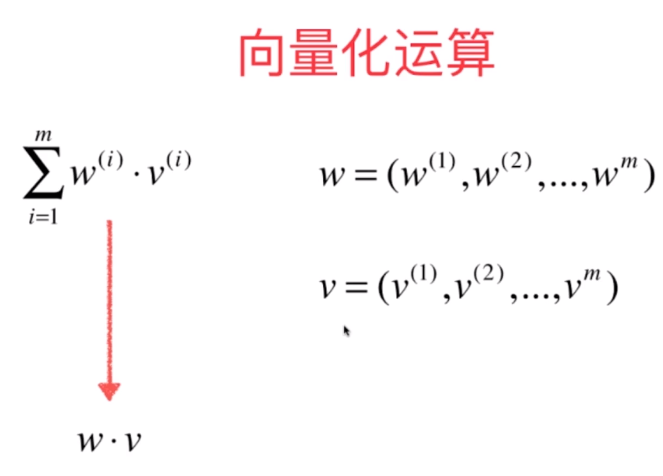
即Linear Regression

介绍

只能用来解决回归问题，也就是预测连续的数值值。前提是假设数据具有线性关系。

回归问题与分类问题在二维坐标轴上的表示方法是不一样的。分类问题可以展现两个特征，而回归问题只能展现一个特征，另一个坐标轴被标记占用了。这是因为在回归问题中，要预测的是具体的数值，这个具体的数值是在一个连续的空间里的，不是简单的可以用不同的颜色代表不同的类别。

如下：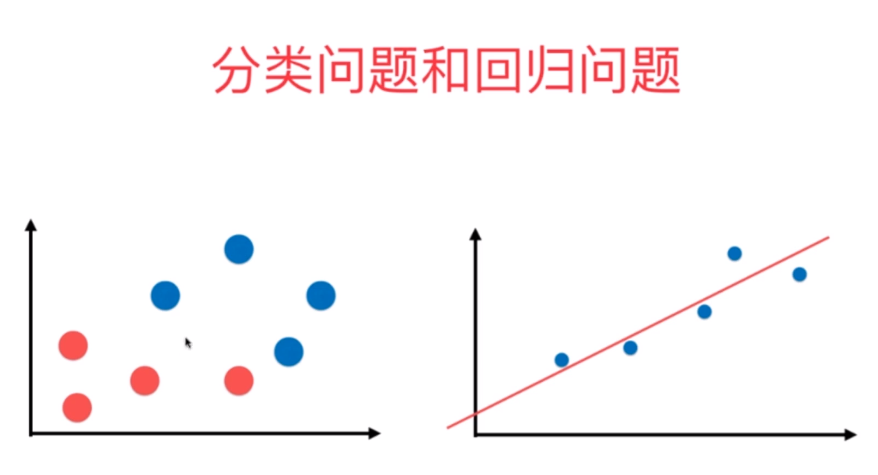

而特征只有一个的线性回归，我们称之为简单线性回归(一元线性回归)。如果特征有两个，就需要在三维的空间中可视化了，有两个或多个特征时叫做多元线性回归。
在简单线性回归中，我们需要寻找一条直线来最大程度的拟合样本特征和样本输出标记之间的关系。

如下：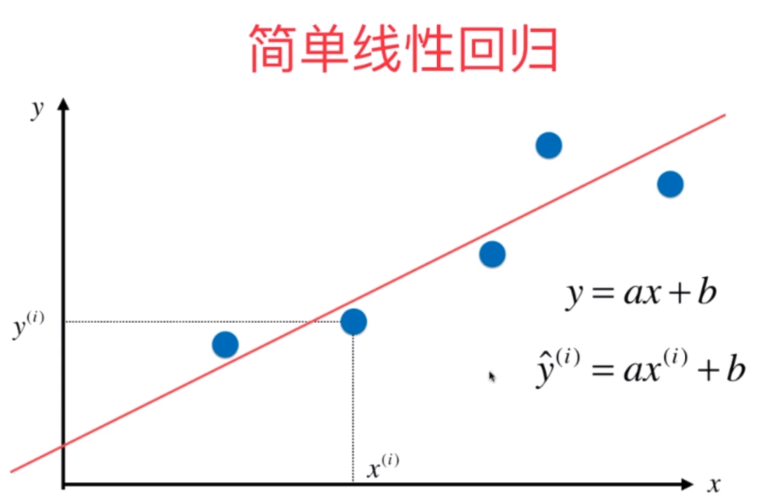

上图：是当样本的特征值带入方程后得出的预测值。此时每一个样本点的真实值可以用表示。

注：读作y hat i，或y小帽子i

线性回归优点

• 思想简单，容易实现
• 是很多非线性模型的基础，例如svm，逻辑回归，多项式回归
• 具有很好的可解释性（白盒子算法）
  • 怎么理解：求出的系数coef的绝对值大小代表了该特征对样本标记的影响程度，coef为正则是正相关，为负是负相关。

假设我们要预测的是boston的房价 boston.feature_names[np.argsort(lin_reg.coeg_)] ，就能得到影响从小到大的排序的特征列

• 蕴含机器学习中的很多重要思想

pass

如何实现线性回归

预测值与真实值之间的误差可以直接由得出，但是向量直接相减求和有弊端，即相减得出的值有正有负，会相互抵消。

于是我们想到求绝对值：

但是这个方法不行，因为绝对值不是一个处处可导的函数：
见下方a，b系数的推导

所以可以采用如下方式：

我们的目标就是使得上述公式最终结果尽可能的小，对其进行演变：

因为 所以

目标函数

也就是当坐标轴上所有的点到拟合直线的距离的平方加起来最短时，即预测误差加起来为最小值时，该直线就是简单线性回归最优解。这是一个典型的 损失函数 (loss function)，也就是用来度量出该模型没有拟合到样本标记的数值，越小越好， 效用函数 (utility function)则相反。有的问题需要用损失函数，有的问题需要用效用函数，而求最小值或最大值的过程称之为，目标函数的最优化。通过最优化目标函数来获得机器学习的模型，有参数学习基本上都是这个套路。

求上述损失函数最小值的问题 是一个典型的最小二乘法的思路可以解决的问题(即求最小化 误差的平方这样的问题)。

PS：最小二乘法思路即对每一个变量求导最终让导数为0，求得极值（划掉，看不懂

公式及其推导过程（待补充）

过程：

损失函数可以用来表示
数学上常用大表示损失函数，而求损失函数的最小值就是求函数的极值

==========================================

简单线性回归！类实现

import numpy as np 
class SimpleLinerRegression1:
    def __init__(self):
        """初始化 Simple  Linear Regression 模型"""
        self.a_ = None
        self.b_ = None
    def fit(self,x_train,y_train):
        """根据训练数据集x_train,y_train训练Simple Linear Regression模型"""
        assert x_train.ndim == 1,\
            "Simple Linear Regression can only solve single feature training data"
        assert len(x_train == len(y_train)),\
            "The size of x_train must be eqal to the size of y_train"
        x_mean = np,mean(x_train)
        y_mean = np.mean(y_train)
        num = 0.0  # 代表分子numerator 
        d = 0.0  # 代表分母denominator
        for x, y in zip(x_train, y_train):
            num += (x - x_mean) * (y - y_mean)
            d += (x - x_mean) ** 2
        self.a_ = num / d
        self.b_ = y_mean - self.a_ * x_mean
        return self
    def predict(self,x_predict):
        """给定待预测数据集x_predict，返回表示x_predict的结果向量"""
        assert x_predict.ndim == 1,\
            "Simple Linear Regression can only solve single feature training data"
        assert self.a_ is not None and self.b_ is not None,\
            "must fit before predict!"
        return np.array([self._predict(x) for x in x_predict])
    def _predict(self,x_single):  # single是单个的意思
        """给定单个待预测数据x_single，返回x_single的预测结果集"""
        return self.a_ * x_single + self.b
    def __repr__(self):
        return "SimpleLinearRgression1()"

调用上述类

from MLplay.SimpleLinearRegression import SimpleLinearRegression1
from sklearn import pyplot as plt
x = np.array([1., 2., 3., 4., 5])
y = np.array([1., 3., 2., 3., 5.])
reg1 = SimpleLinearRegression1()
reg1.fit(x, y)
x_predict = 6
print(reg1.predict(np.array([x_predict])))  # 输出预测值
print(reg.a_, reg.b_)  # 输出参数模型的a和参数b
"""绘制图片"""
y_hat1 = reg.predict(x)
plt.scatter(x, y)
plt.plot(x, y_hat1, color='r')
plt.axis([0,6,0,6])  # 限制x轴和y轴的范围在0~6之间
plt.show()

简单线性回归随机生成样本标签和样本特征

m = 1000000
x = np.random.random(size=m)
y = x * 2.0 + 3.0 + np.random.normal(size=m)

类实现_向量化运算版

在“简单线性回归！类实现”中我们使用了循环的方式求 a 的值，但是这样性能效率比较低，转化成向量运算性能效率会大大提高。

import numpy as np 
from sklearn.metrics import r2_score
class SimpleLinerRegression2:   #==================================改动
    def __init__(self):
        """初始化 Simple  Linear Regression 模型"""
        self.a_ = None
        self.b_ = None
    def fit(self,x_train,y_train):
        """根据训练数据集x_train,y_train训练Simple Linear Regression模型"""
        assert x_train.ndim == 1,\
            "Simple Linear Regression can only solve single feature training data"
        assert len(x_train == len(y_train)),\
            "The size of x_train must be eqal to the size of y_train"
        x_mean = np,mean(x_train)
        y_mean = np.mean(y_train)
#===================================================================================================改动
        num = (x_train - x_mean).dot(y_train -y_mean)   # dot用于向量相乘求内积，直接相乘的话还是返回一个向量
        d = (x_train - x_mean).dot(x_train - x_mean)
# =========================================================================================================改动
        self.a_ = num / d
        self.b_ = y_mean - self.a_ * x_mean
        return self
    def predict(self,x_predict):
        """给定待预测数据集x_predict，返回表示x_predict的结果向量"""
        assert x_predict.ndim == 1,\
            "Simple Linear Regression can only solve single feature training data"
        assert self.a_ is not None and self.b_ is not None,\
            "must fit before predict!"
        return np.array([self._predict(x) for x in x_predict])
    def _predict(self,x_single):  # single是单个的意思
        """给定单个待预测数据x_single，返回x_single的预测结果集"""
        return self.a_ * x_single + self.b
    def score(self, x_test,y_test):
        """根据测试集数据 x_test 和 y_test 确定当前模型准确度"""
        y_predict = self.predict(x_test)
        return r2_score(y_test,y_predict)
    def __repr__(self):
        return "SimpleLinearRgression2()" # =================================改动

多元线性回归(可以先看下面的内容)

在我们上述的描述中，简单线性回归是一个只有单个特征的样本。所拟合的直线如下：
，此时若把看作一个向量，则：

即数据集的第行的第一个特征到最后一个特征

推导得出：

即某一数据集矩阵中的每一列特征被映射为，截距则变成相应的，系数为什么变成不同的 ，很好解释，不同的特征对于模型的影响不同，系数自然也不一样。

由上可知： 表示只有一个特征列的情况。

想要多元线性回归的准确度最高，我们同样使用简单线性回归模型的损失函数来求最最小值：

为什么是大而不是原来的小，因为我们需要取数据集的第行样本的每一个特征分别带入已经求出参数的模型（公式）中去，得出预测的标签值（y）。也就是说表示的是遍历每一个样本的 特征向量 。又是怎么出现的？答：是虚构的特征，恒等于1。

所代表的系数向量和所代表的遍历每个样本的特征向量则可以这么表示：

# 转置成列向量

# 第i个样本的特征向量

得出：
# 向量相乘（点乘，求内积）

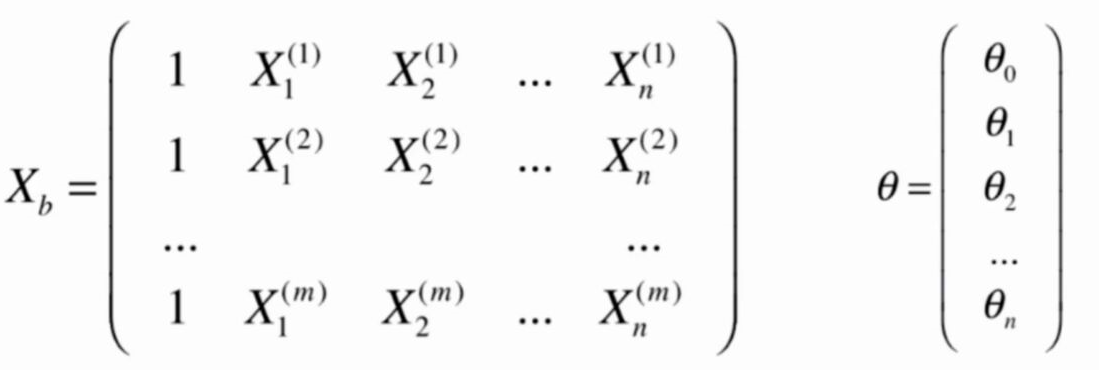
上述矩阵就是所代表的含义，那为什么要叫，为了区分：
代表原矩阵，代表加了虚构特征列（恒为1）的矩阵。

，结合上图，矩阵和向量乘法，同序号行列中的每一项分别相乘最后相加（所以列要=行），然后行定列动，列尽行动，图中是列是向量，只有一列，所以直接行动。

则损失函数可以进行矩阵运算的演化：

最后我们同样使用简单线性回归的最小二乘法的思路，求出

公式及其推导过程（待补充）:
是一个对矩阵求导的推导过程，超出本科线性代数范围，不学了

公式结果：

这个式子称为多元线性回归的正规方程解（Normal Equation）

但是这个求解的时间复杂度非常高

线性回归没有量纲问题，不需要进行数据的归一化

多元线性回归类实现

import numpy as np
from sklearn.metrics import r2_score
class LineargRression:
    def __init__(self):
        """初始化Linear Regression模型"""
        self.coef_ = None  # coefficient系数，是一个theta向量
        self.interception_ = None  # 截距
        self._theta = None  # 私有化属性theta，包括截距的系数
    def fit_normal(self, X_train, y_train):
        """根据训练数据集X_train, y_train训练Linear Regression 模型"""
        assert X_train.shape[0] == y_train.shape[0],\
            "the len of X_train must be equal to the lne of y_train"
        X_b = np.hstack([np.ones(len(X_train), 1),X_train])
        self._theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)
        self.interception_ = self._theta[0]
        self.coef_ = self._theta[1:]
        return self
    def predict(self, X_predict):
        """给定待预测的X_predict，返回表示X_predict预测值的结果向量"""
        assert self.coef_ is not None and self.interception_ is not None,\
        "must fit before predict!"
        assert X_predict.shape[1] == len(self.core_),\
            "the feature number of X_predict must be equal to X_train"
        X_b = np.hstack([np.ones(len(X_predict),1), X_predict])
        return X_b.dot(self._theta)
    def score(self, X_test, y_test):
        """根据测试数据集 X_test 和 y_test 确定当前模型的准确度"""
        y_predict = self.predict(X_test)
        return r2_score(y_test, y_predict)
    def __repr__(self):
        return "Linear Regression()"

线性回归算法的评测

KNN可以用accuracy_score度量分类的准确度，简单线性回归则任然采用求损失函数最小值的方式对算法进行评测。简单线性回归的损失函数公式其实是基于训练集的，因此我们要求基于测试集的损失函数最小值。如下

但是这个衡量标准是和m相关的，所以：

是为了排除测试数据集样本数量的干扰，方便比较最终的数值。

MSE(Mean Squared Error)

即均方误差，如上的公式，怎么理解？答：误差的平方和的平均值

RMSE(Root Mean Squared Error)

即均方根误差，为了解决量纲上的问题，假设标记y为房价，单位是万元，则y的量纲是万元，而MSE得出的量纲是万元的平方。所以我们把MSE开根号，使均方误差和样本标记在同一量纲上，可以更好的解释与真实值的平均误差。公式如下：

均方根误差和均方误差本质上一样的，只不过前者所能体现的误差背后的意义更加明显，即可以更好的解释与真实值的平均误差。

MAE(Mean Absolute Error)

平均绝对误差

通常RMSE会比MAE更大，这是由该式子的数学性质决定的，举例如下

假设有一组向量数据的值 ： [ [1,1,2,100] ]
则MAE = （1+1+2+100）/ 4 = 26
RMSE = (1+1+4+10000) / 4 = 2501.5 再开根号，差距一目了然，结论如下：

因为RMSE求解的方式含有平方，单个误差呈二次增长，会放大错误的样本特征。所以当MAE与RMSE的值越接近时，说明样本中没有偏离拟合直线较远的点，这是选取目标函数时使用带平方的式子表现出的另一重优势。

在定义损失函数时没有采用这种形式，是因为它不是一个处处可导的函数，而评价算法时使用这种形式是因为系数a，b已经被求出来了，不再需要处处可导的条件？

函数上实现三种测评方法

import numpy as np 
from math import sqrt
def mean_squared_error(y_true, y_predict):
    """计算y_true和y_predict之间的MSE"""
    assert len(y_true) ==len(y_predict),\
        """The size of y_true must be eqal to the size of y_predict"""
    return np.sum((y_predict - y_true) ** 2) / len(y_true)
def root_mean_suqared_error(y_true,y_predict):
    """计算y_true和y_predict之间的RMSE"""
    return sqrt(mean_squared_error(y_true, y_predict))
def mean_abslute_error(y_true,y_predict):
    """计算y_true和y_predict之间的MAE"""
    assert len(y_true) == len(y_predict),\
        """The size of y_true must be eqal to the size of y_predict"""
    return np.sum(np.abs(y_true - y_predict)) / len(y_true)

sklearn实现MSE和MAE

模型评估

R Squared(最重要)

即R方：
当我们用RMSE或MAE求出误差最小值以后，会难以比较线性回归作用在哪种问题的预测上比较准确。分类问题可以简单的比较准确度分数，但是回归问题则无法度量，举个例子，房价预测的平均误差在5w，学生成绩预测的平均误差在10分，这是两种不同的东西，你不能用来比较预测的准确度。

所以用R方公式：

Residual Sum of Squares Total Sum of Squares

演化如下：

上述式子的分子是预测值与真实值的误差，分母是平均值与真实值的误差，这个平均值可以看成一个简单的模型，即不论你放什么样本去预测，得到的标记数值都是测试数据集样本标记数值的平均值，在机器学习或统计学领域把这种模型叫做Baseline Model。那么我们的由目标函数最优化得到参数a，b，然后构建的模型预测出的数值必然是比Baseline Modle预测的准确率要高。也就是分子式子求出的误差小于分母式子求出的误差，分子需要小于分母，如果分子大于分母，说明你训练得出的模型烂透了。

由上述描述可知：

• R^2 <= 1
• R^2越大越好，当我们的模型不凡任何错误，也就是误差为0时，R^2可以得到最大值1
• 当我们的模型和基准模型（Baseline Model）一样烂的时候，R^2等于0
• 如果R^2小于0，说明我们学到的模型不如基准模型。此时，可能说明我们的数据不具有线性关系
  

由式子推演可得上述的结果。

函数上实现R squared

from sklearn.mertrics import mean_squared_error
def r2_score(y_true,y_predict):
    """计算y_test和y_predict之间的 R squared"""
    return 1 - mean_squared_error(y_true,y_predict) / np.var(y_true)

sklean实现R squared

模型评估