K-means
首先,我们需要确定簇的个数,作为模型的参数,
但这样效果不好,可以用遍历来指定一个范围的簇的个数,比较轮廓系数或者绘图观察,得出结论。当然直接用肉眼观察图表的方式也可以选定簇的个数,仅限二维和三维的数据。
当我们选定簇的个数后,需要为这些假定的簇(即假定了几个簇)随机初始化一个各自的聚类质心点(cluster centroids),你不知道这些簇的初始聚类中心点会被放在哪,在下图中被表示为X,然后我们分别计算每一个数据点到质心的距离,比较每一个数据样本到每一个质心的距离,样本离哪个聚类的质心更近,该样本就被划分到该聚类。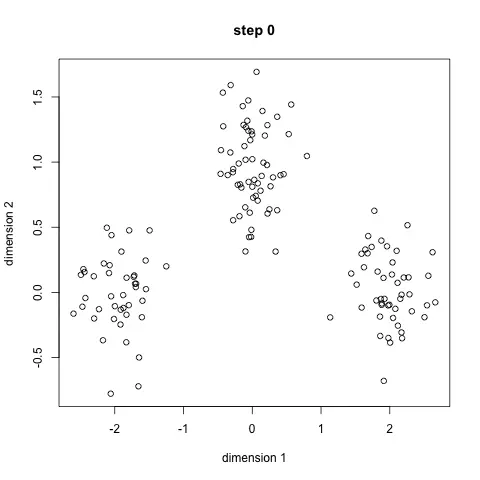
当然了,初始质心并不是真正的质心,质心应该满足簇中的每个点到它的欧式距离平方和最小这个条件,因此,根据这些被初步分类完毕的数据点,我们再重新计算每一聚类中所有向量的平均值,并确定出新的质心。该向量指的是特征向量。
最后,重复上述步骤,进行一定次数的迭代,直到质心的位置不再发生太大变化。
sklearn使用K-means
https://blog.csdn.net/lynn_001/article/details/86679270(sklearn K-Means使用小结,非常详细)
https://zhuanlan.zhihu.com/p/96729670(参考,感觉用处不大,本文档摘取第一段传统k-means的使用)
K均值
K值的评估
有轮廓系数(Silhouette Coefficient)和Calinski-Harabasz Index以及用绘图展现的手肘法
手肘法
- 核心指标:SSE(sum of the squared errors,误差平方和)
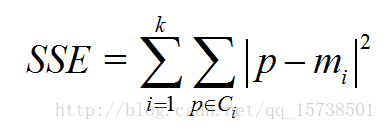
- Ci是第i个簇
- p是Ci中的样本点
- mi是Ci的质心(Ci中所有样本的均值)
-
-手肘法核心思想
随着聚类数k的增大,样本划分会更加精细,每个簇的聚合程度会逐渐提高,那么误差平方和SSE自然会逐渐变小。
- 当k小于真实聚类数时,由于k的增大会大幅增加每个簇的聚合程度,故SSE的下降幅度会很大,而当k到达真实聚类数时,再增加k所得到的聚合程度回报会迅速变小,所以SSE的下降幅度会骤减,然后随着k值的继续增大而趋于平缓,也就是说SSE和k的关系图是一个手肘的形状,而这个肘部对应的k值就是数据的真实聚类数。 ```python import pandas as pd from sklearn.cluster import KMeans import matplotlib.pyplot as plt
dffeatures = pd.read_csv(r’C:\预处理后数据.csv’,encoding=’gbk’) # 读入数据 ‘利用SSE选择k’ SSE = [] # 存放每次结果的误差平方和 for k in range(1,9): estimator = KMeans(n_clusters=k) # 构造聚类器(estimator:估计器) estimator.fit(df_features[[‘R’,’F’,’M’]]) SSE.append(estimator.inertia) # estimator.inertia_获取聚类准则的总和. X = range(1,9) plt.xlabel(‘k’) plt.ylabel(‘SSE’) plt.plot(X,SSE,’o-‘) plt.show()
<a name="ZwGhM"></a>## 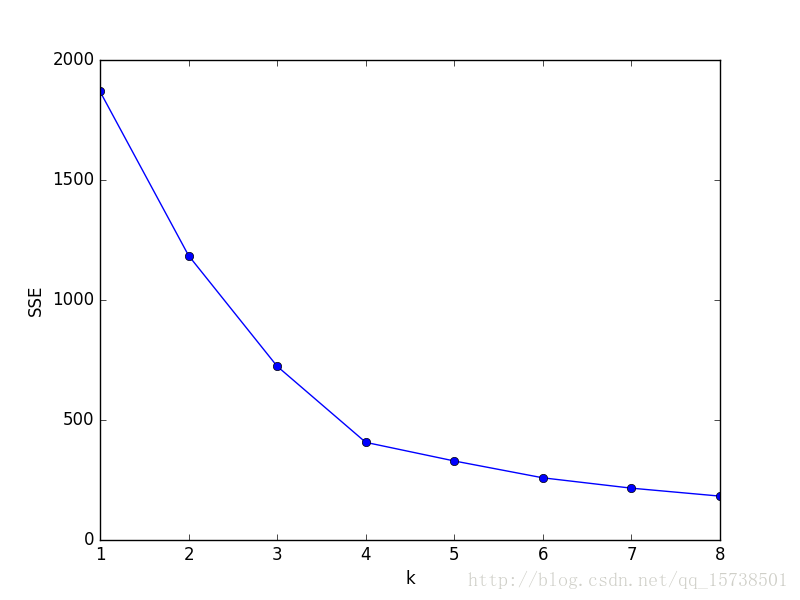<a name="a1ldA"></a>## 轮廓系数法[b站轮廓系数法](https://www.bilibili.com/video/BV1B7411R7NA?from=search&seid=11564573819655101677)<br />使用轮廓系数(silhouette coefficient)来确定,**选择使系数较大所对应的k值**<br />方法:- 计算样本i到同簇其他样本的平均距离,定义为为样本i的**簇内不相似度**。ai 越小,说明样本i越应该被聚类到该簇。<br />簇C中所有样本的均值称为簇C的簇不相似度。- 计算样本i到其他某簇 的所有样本的平均距离,分别和所有的簇进行计算,取最小的,称为样本i的**簇间不相似度**。<br />bi越大,说明样本i越不属于其他簇。- 根据样本i的簇内不相似度a i 和簇间不相似度b i ,定义样本i的轮廓系数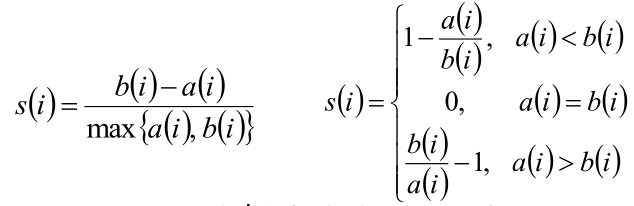<br />公式解读:簇间不相似度-簇内不相似度,然后除以簇间不相似度和簇内不相似度中比较大的那个值。最后再把所有s求均值就是轮廓系数了。- 判断:<br />轮廓系数范围在[-1,1]之间。该值越大,越合理。<br />si接近1,则说明样本i聚类合理;<br />si接近-1,则说明样本i更应该分类到另外的簇;<br />若si 近似为0,则说明样本i在两个簇的边界上。- 所有样本的s i 的均值称为聚类结果的轮廓系数,是该聚类是否合理、有效的度量。- 使用轮廓系数(silhouette coefficient)来确定,选择使系数较大所对应的k值- [sklearn.metrics.silhouette_score](http://scikit-learn.org/stable/modules/generated/sklearn.metrics.silhouette_score.html) sklearn中有对应的求轮廓系数的API```pythonimport numpy as npfrom sklearn.cluster import KMeanskmeans_model = KMeans(n_clusters=3, random_state=1).fit(X)labels = kmeans_model.labels_metrics.silhouette_score(X, labels, metric='euclidean')# out:0.55...

