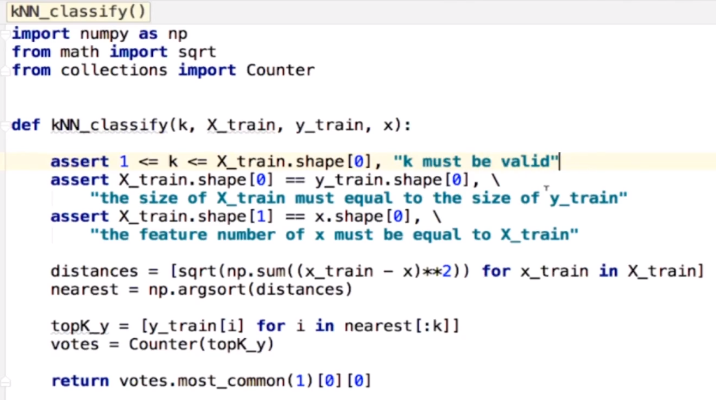
介绍

K-Nearest Neighbors，简称 KNN ，是一种无参模型。主要解决分类问题，不建议解决回归问题。
假设在一个特征空间中分布着很多由特征组成的带有标记的样本，此时新来了一个拥有同样特征数量但没有标记的样本，该如何确定他的标记？取离这个样本最近的k个点，其中这个k是一个变量，这k个点进行投票，种类最多的样本获胜，然后新样本被归类到该标记中。

案例

如如下图所示，在这个特征空间中有绿色样本和红色样本,此时我们要预测这个蓝色样本属于哪个样本类别。需要计算蓝色样本与每一个样本的距离，并得出最近的几个样本是什么类别。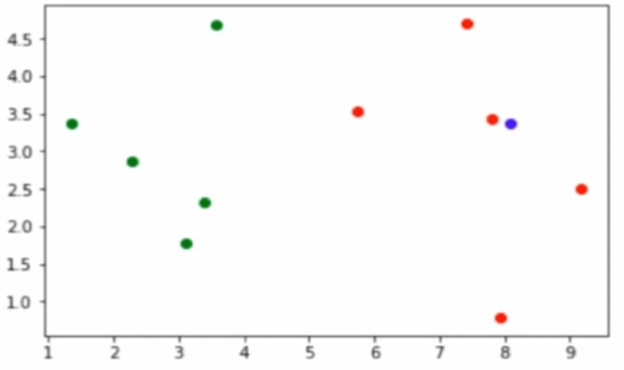
image.png

缺点

最大的缺点是效率低下，因为 模型就是数据本身 ，所以每次预测样本分类时需要计算每个样本与新来点的距离。而每个样本又要用n个特征去计算。可以使用树结构进行优化：KD-Tree，Ball-Tree

缺点2：得到的结果高度数据相关，对异常值高度敏感，比如k取3时，最近的样本有俩个是异常的，就分类错误了。

缺点3：预测结果不具有解释性，你只是知道这些样本之间距离近，就把他们归为一类，却不知道具体是什么原因

缺点4：维数灾难，随着维度的增加，“看似相近”的俩个点之间的距离会越来越大
例子：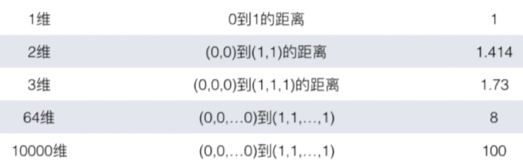
image.png

KNN三要素

k值
距离度量
超参数algorithm：ball_tree，kd_tree(基于欧氏距离，低于二十维度时优化不错)，暴力搜索，auto
分类规则

超参数

超参数的的具体概念请移步 ./其他/超参数

K：也就是设定最近邻居的个数，sklearn封装算法中K超参数对应“n_neighbors= ”必须填入一个具体的数值

距离加权：可以用来解决平票的问题，即k个样本投票后，每个种类的票数一致的情况，当然也可以单纯在调参时使用。距离加权通常是以直接选取距离的倒数的方法作为计算权重的方式，比如距离是1，加权后还是1；距离是5时，加权后就是1/5。在sklearn封装算法中距离加权超参数对应“weights=” 默认是“weights=uniform”，uniform是统一的，一致的意思，即平权，每个样本的票权重一样的意思。当“weights=distance”就是距离加权。

距离计算方式：对应sklearn算法中的“p=”，默认是2

距离计算的具体公式移步 ./前置内容/距离计算/高中数学及其拓展/距离计算

KNN的调库表达

K近邻算法

KNN自建类（仿sklean接口设计）

  1. import numpy as np
  2. from math import sqrt
  3. from collections import Counter
  4. from .metrics import accuracy_score
  6. class KNNClassifier:
  7.     def __init__(self, k):
  8.         """初始化KNN分类器"""
  9.         assert k >= 1,"k must be valid"  # k必须是合法的
  10.         self.k = k
  11.         self._X_train = None
  12.         self._y_train = None
  14.     def fit(self, X_train, y_train):
  15.         """根据训练数据集X_train和y_train训练KNN分类器"""
  16.         assert X_train.shape[0] == y_train.shape[0],\
  17.             "the size of X_train must be eqal to the size of y_train"
  18.         assert self.k <= X_train.shape[0],\
  19.             "the size of X_train must be at leask k."
  21.         self._X_train = X_train
  22.         self._y_train = y_train
  23.         return self
  25.     def predict(self, X_predict):
  26.         """给定待预测数据集X_predict，返回表示X_predict的结果向量"""
  27.         assert self._X_train is not None and self._y_train is not None,\
  28.             "must fit before predict!"
  29.         assert X_predict.shape[1] == self.X_train.shape[1],\
  30.             "the fearure number of X_predict"
  32.         y_predict = [self._predict(x) for x in X_predict]
  33.         return np.array(y_predict)
  35.     def _predict(self, x):
  36.         """给定单个待预测数据x，返回x的预测结果值"""
  37.         assert x.shape[0] == self._X_train[1],\
  38.             "the feature number of x must be eqal to X_train"
  40.         distances = [sqrt(np.sum((x_train - x) ** 2))
  41.                     for x_train in self._X_train]
  42.         nearest = np.argsort(distances)
  44.         topK_y = [self._y_train[i] for i in nearest[:self.k]]
  45.         votes = Counter(topK_y)  # 返回一个counter字典，键是每一个种类，值是该种类的个数
  47.         return votes.most_common(1)[0][0]  """参数1表示取前1个最多出现的标记，most_common返回的是一个元组列表，\
  48.                                     第一个元素代表出现最多的标记，元组里有俩个数据，第一个数据是种类，第二个数据代表出现了几次"""
  49.     def score(self, X_test, y_test):
  50.         """根据测试集 X_test 和 y_test 确定当前模型的准确度"""
  51.         y_predic = self.predict(X_test)
  52.         return accuracy_score(y_test, y_predict)
  54.     def __repr__(self):  """自定义输出实例化对象时展示的信息，而不是<__main__.XXX object at 0x000001A7275221D0>,\
  55.                                 类名+object at+内存地址"""
  56.         return "KNN(k=%d)" % self.k

KNN的算术表达（面条版本）

  1. # KNN的算术表达
  3. from matplotlib import pyplot as plt 
  4. import numpy as np 
  5. from math import sqrt 
  6. from collections import Counter
  8. np.random.seed(1)
  9. feature1 = np.random.randint(0,20,size=10)
  10. np.random.seed(2)
  11. feature2 = np.random.randint(0,20,size=10)
  13. label = np.array([0,0,0,0,0,1,1,1,1,1])
  15. # 新传入的点
  16. x = np.array([15,6])
  18. plt.scatter(feature1[label==0], feature2[label==0])
  19. plt.scatter(feature1[label==1], feature2[label==1])
  20. plt.scatter(x[0],x[1])
  21. #plt.show()
  23. distance= []
  24. # 计算欧拉距离,下面是帮助你理解的简易式子：
  26. # ts = np.array([2,3])
  27. # ts1 = np.array([5,6])
  28. # print(sum((ts - ts1)**2))  # 即sum(9,9) 
  30. for i,j in zip(feature1,feature2):
  31.     '''
  32.     也可以不用for直接使用列表生成式的方式
  33.     distance = [sqrt((i - x[0])**2 + (j - x[1])**2) for i,j in zip(feature1,feature2)]
  34.     '''
  35.     d = sqrt((i - x[0])**2 + (j - x[1])**2)
  36.     distance.append(d)
  38. distance = np.array(distance)
  39. d_sort = distance.argsort()
  41. #设置邻居的个数
  42. k = 6
  44. near_n = [label[i] for i in d_sort[:k]]
  45. votes = Counter(near_n)
  46. '''
  47. votes的输出值为 Counter({0: 4, 1: 2}) ，表示0有4个，1有两个
  48. '''
  50. most_common = votes.most_common(1) # 参数用来指定最频繁出现的几个数，当前参数值为1
  51. '''
  52. most_common 的输出值为[(0, 4)]
  53. 表示最常出现的一个数是0，出现了四次
  54. '''
  56. x_kind = most_common[0][0]
  58. print(f'x用KNN预测归属于第{x_kind}种类')

KNN分类函数模拟

image.png
PS：看类实现和sklearn实现即可

KNC调库实现