层次聚类博文
博文+1
又被称为hierarchical agglomerative clustering（HAC，层次凝聚聚类），是一个自下而上的层次化聚类算法。首先会将每个数据点视为单个聚类，然后连续合并（或聚合）成对的聚类，直到所有聚类合并成包含所有数据点的单个聚类。该算法的聚类可以被表示为一幅树状图，树根是最后收纳所有数据点的单个聚类，而树叶则是只包含一个样本的聚类。

直接看GIF理解：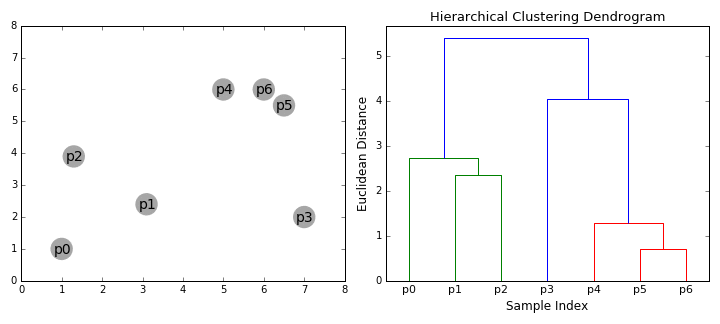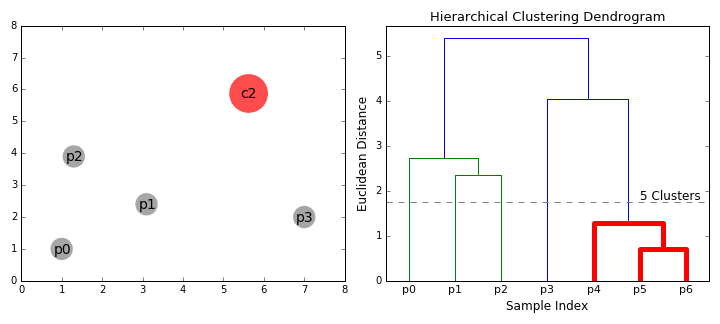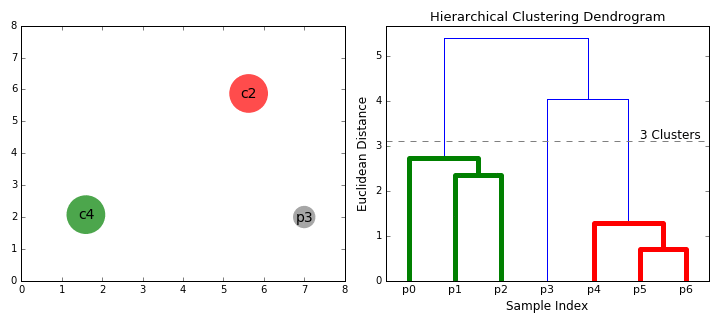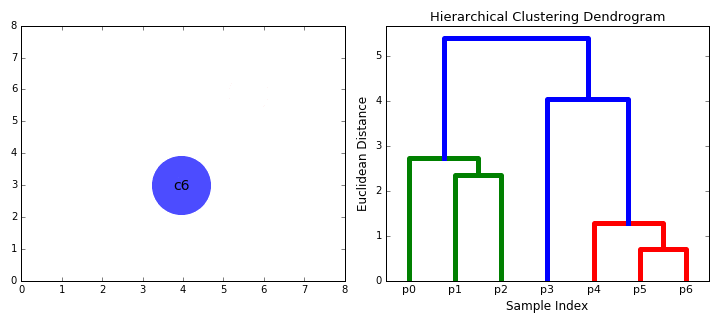

1. 首先，我们把每个数据点看作是一个聚类，即如果数据集中有X个数据点，它就有X个聚类。然后我们设置一个阈值作为衡量两个聚类间距离的指标：如果距离小于阈值，则合并；如果距离大于阈值，迭代终止。
2. 在每轮迭代中，我们会把两个聚类合并成一个聚类。这里我们可以用到average linkage（平均连接，计算簇间距离的方法之一，超参数），它的思路是计算所有分属于两个目标聚类的数据点之间距离，然后求一个平均值。每次我们会根据设定的阈值选取平均距离最小的两个聚类，然后把它们合并起来，因为按照我们的标准，它们是最相似的。
3. 重复步骤2，直到我们到达树根，即最后只有一个包含所有数据点的聚类。通过这种方式，我们可以选择要几个聚类，以及什么时候停止聚类。

层次聚类不要求我们指定聚类的数量，由于这是一个构建树的过程，我们甚至可以选择那种聚类看起来更合适。另外，该算法对距离阈值的选择不敏感，无论怎么定，算法始终会倾向于给出更好地聚类结果，而不像其他算法很依赖参数。根据层次聚类的特点，我们可以看出它非常适合具有层次结构的数据，尤其是当你的目标是为数据恢复层次时。这一点是其他算法无法做到的。与K-Means和GMM的线性复杂性不同，层次聚类的优势是以较低的效率为代价，因为它具有O(n3)的时间复杂度。

sklearn使用HAC

计算聚类簇间距离的方法，也就是超参数Linkage，距离合适就会合并成一个簇：
未完成簇：尚未变成一整个大簇的簇叫做未完成簇。
Single Linkage：方法是将每个未完成簇中距离最近的两个数据点间的距离作为未完成簇的距离。这种方法容易受到极端值的影响。两个不相似的未完成簇可能由于其中的某个极端的数据点距离较近而组合在一起。
Complete Linkage：Complete Linkage的计算方法与Single Linkage相反，将两个未完成簇中距离最远的两个数据点间的距离作为这两个未完成簇簇的距离。Complete Linkage的问题也与Single Linkage相反，两个相似的未完成簇可能由于其中的极端值距离较远而无法组合在一起。
Average Linkage：Average Linkage的计算方法是计算每个未完成簇的每个数据点与其他所有数据点的距离。将所有距离的均值作为两个组合数据点间的距离。这种方法计算量比较大，但结果比前两种方法更合理。
语雀内容