逻辑回归，用回归的模型（预测的值是连续的概率）解决二分类问题。ps：可以用特殊方法解决多分类问题

，放入数据，求出该数据出现的概率，概率大于0.5划分到一类，小于0.5划分到另一类

首先我们引入线性回归的公式，theta是系数，表示在测试样本x中加一个1，用来和theta0相乘。
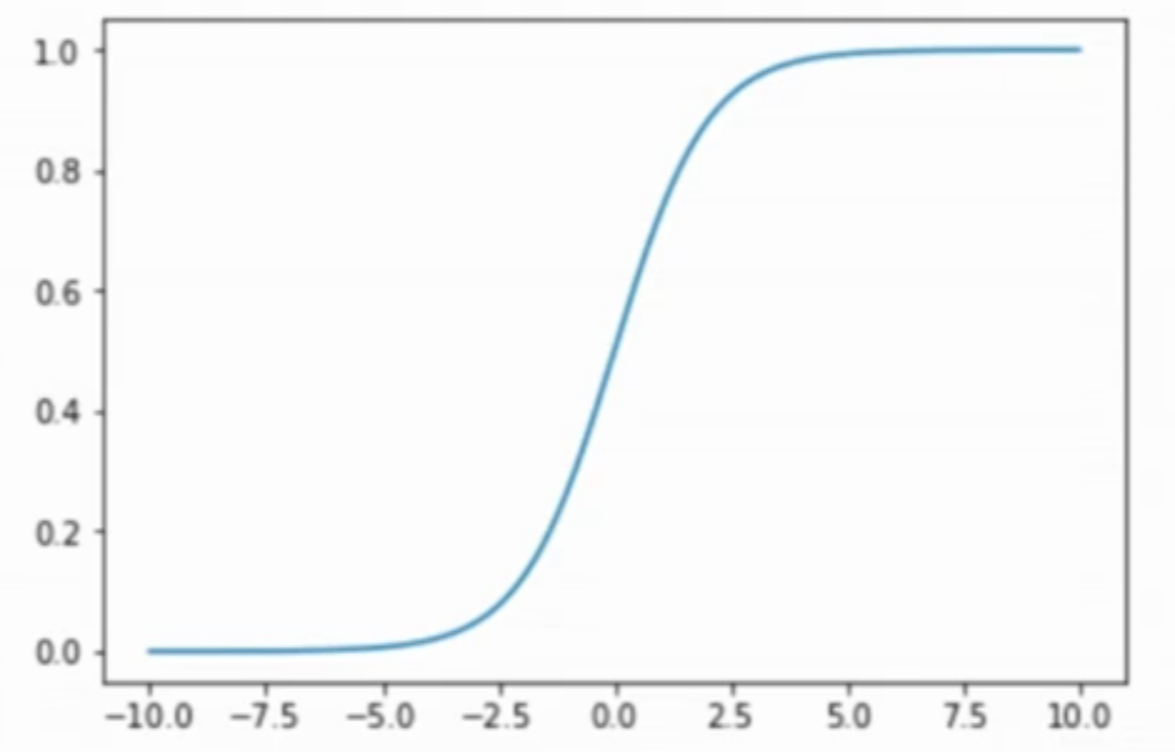
此时y的值域是-inf到+inf，但是概率的值域是[0，1]，所以要用一个函数（sigmoid）把y的值域限定在[0，1]。如下：
，这个，这里的t就是，也就是说当趋向于正无穷的时候，分母趋向于1+0，因为负次方幂的值为正次方幂的倒数。反之趋向于负无穷的时候，分母趋向于1+（+inf）。
下面我们用绘图的形式来直观感受一下。

sigmoid绘图

import numpy as np
import matplotlib.pyplot as plt
def sigmoid(t):
return 1/(1+ np.exp(-t))
x = np.linspace(-10, 10, 500)
y = sigmoid(x)
plt.plot(x, y)
plt.show()

逻辑回归损失函数的定义

当真实样本的分类为1的时候，如果预测出来的概率p越小，说明损失越大，p越大，说明损失越小。

根据，我们衍生出损失函数以及图表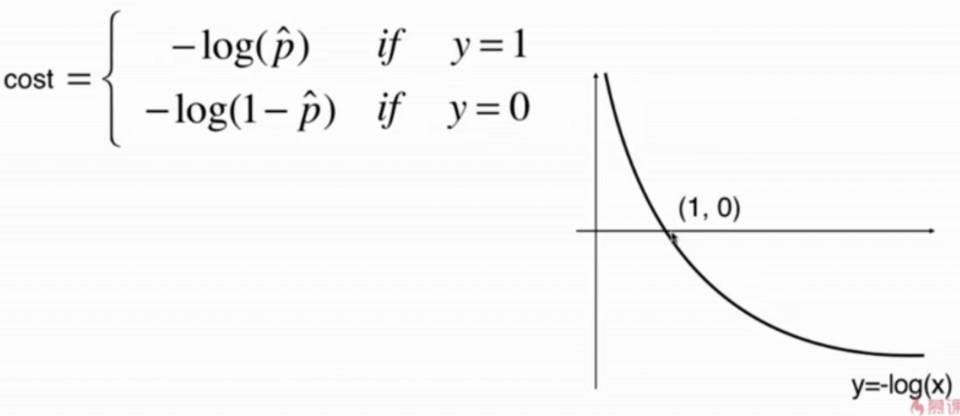

因为我们的概率值域是[0，1]，所以只需要看图表第一象限的函数部分即可。假设真实值是1的时候，x(p值)越小，相应的，损失函数y就越大。

使用两个损失函数太麻烦，所以把这俩个损失函数合并一下：

当真实值y=0时，前面就没了，当y=1时，后半部分就没了
最后损失函数的终极形态就是

其中

然后使用梯度下降法来求theta的损失函数最优化，这是个凸函数，没有局部最优解。
所以我就跳过了求损失函数梯度的步骤

逻辑回归正则化

使逻辑回归也可以处理非线性问题


大相当于线性回归中的，只不过常数加到了原损失函数前面。

sklearn使用逻辑回归

自带正则项，默认是 penalty=’l2’，常数C默认C=’1’

生成并绘制数据

import numpy as np
import matplotlib.pyplot as plt
np.random.seed(666)
X = np.random.normal(0, 1, size=(200, 2))
y = np.array((X[:,0]**2+X[:,1])<1.5, dtype='int')  # 小于1.5的分类为1，大于的分类为0
'''随机取20点变成分类1，也就是噪音'''
for _ in range(20):
    y[np.random.randint(200)] = 1
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.show()
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)

解决线性问题

from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression()
log_reg.fit(X_train, y_train)
log_reg.score(X_test, y_test)

解决非线性问题

from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
def PolynomialLogisticRegression(degree, C, penalty='l2'):
    return Pipeline([
        ('poly', PolynomialFeatures(degree=degree)),
        ('std_scaler', StandardScaler()),
        ('log_reg', LogisticRegression(C=C, penalty=penalty))
    ])
poly_log_reg4 = PolynomialLogisticRegression(degree=20, C=0.1, penalty='l1')
poly_log_reg4.fit(X_train, y_train)
poly_log_reg4.score(X_test, y_test)

逻辑回归解决多分类问题

OVO

每次只挑出俩个类别，看新来一个样本分到哪个分类，如有有四个类别，就能形成6种不同的组合，然后投票，看在哪个类别中出现的次数最多。

，套用组合计算公式。
，叹号表示阶乘。

还有排列计算公式
n个类别就需要C(n,2)次分类。但是相对的预测准确度也更高。

OVR

把一个种作为一类，其余的作为另一类，就变成了二分类问题。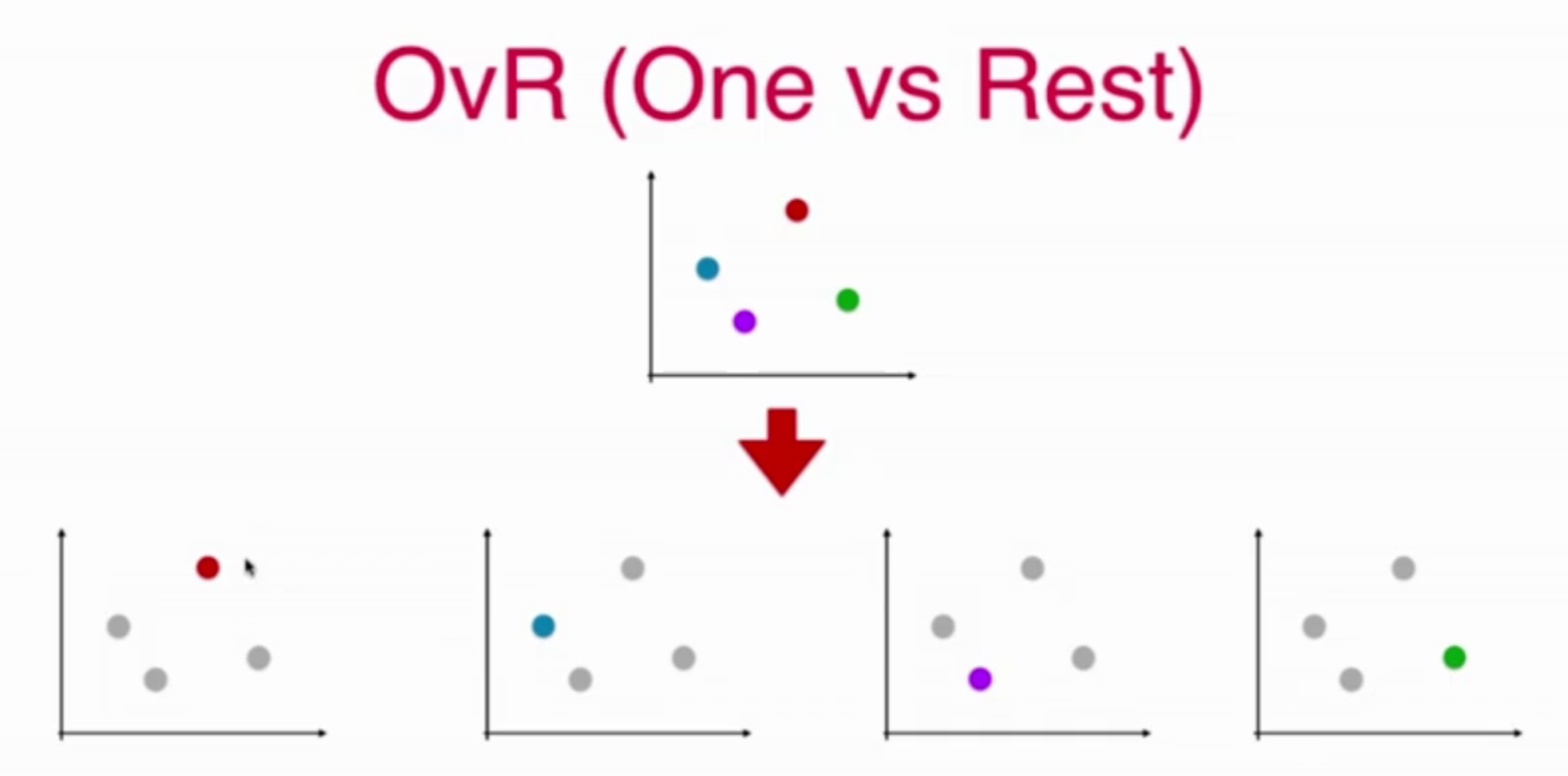

依次把每种分类作为一个类别，其余点作为另一个类别，最后就的到了每个分类出现的概率
n个类别就需要n次分类。

sklearn.LogisticRegression中的ovo和ovr

multi_class参数决定了我们分类方式的选择，有 ovr和multinomial两个值可以选择，默认是 ovr。
ovr即前面提到的one-vs-rest(OvR)，而multinomial即前面提到的many-vs-many(MvM)。如果是二元逻辑回归，ovr和multinomial并没有任何区别，区别主要在多元逻辑回归上。
OvR的思想很简单，无论你是多少元逻辑回归，我们都可以看做二元逻辑回归。具体做法是，对于第K类的分类决策，我们把所有第K类的样本作为正例，除了第K类样本以外的所有样本都作为负例，然后在上面做二元逻辑回归，得到第K类的分类模型。其他类的分类模型获得以此类推。
而MvM则相对复杂，这里举MvM的特例one-vs-one(OvO)作讲解。如果模型有T类，我们每次在所有的T类样本里面选择两类样本出来，不妨记为T1类和T2类，把所有的输出为T1和T2的样本放在一起，把T1作为正例，T2作为负例，进行二元逻辑回归，得到模型参数。我们一共需要T(T-1)/2次分类。
从上面的描述可以看出OvR相对简单，但分类效果相对略差（这里指大多数样本分布情况，某些样本分布下OvR可能更好）。而MvM分类相对精确，但是分类速度没有OvR快。
如果选择了ovr，则4种损失函数的优化方法liblinear，newton-cg, lbfgs和sag都可以选择。但是如果选择了multinomial,则只能选择newton-cg, lbfgs和sag了。

sklearn中的ovo和ova拓展

对于任意二分类算法都可以拓展成多分类算法