常见的统计变量
常见的概率分布
重要概率公式
协方差与相关系数
可以控制测量的自变量，叫做变量也叫做因子。与自变量有关，但数值不可以控制，随机变化的较做因变量（响应）。
https://www.bilibili.com/video/BV18E411L74e
https://www.bilibili.com/video/BV1eC4y1H77r?from=search&seid=10844867807796617662
偏差：偏差又称为表观误差，是指个别测定值与测定的平均值之差，它可以用来衡量测定结果的精密度高低[1]。在统计学中，偏差可以用于两个不同的概念，即有偏采样与有偏估计。一个有偏采样是对总样本集非平等采样，而一个有偏估计则是指高估或低估要估计的量
‘’’
概率介绍
概率论是统计学的基础，统计学冲锋在应用第一线，概率论为统计学提供武器。
统计学可以分为描述统计学和推断统计学，前者用特定数字或图表来描述数据总体的离散或集中趋势，后者用小样本数据推断总体数据。
集中趋势的描述有：中位数，众数，平均值
- 中位数对数据变化不够敏感，众数不一定具有唯一性，平均值受极端值影响大
离散趋势的描述有：极差，方差，标准差
- 极差的描述比较粗糙
- 总体方差公式
，方差是用来描述数据的离散程度的 - 样本方差公式
，研究整体中的一部分的方差
图表描述：
- 频数直方图：频数（数据出现的次数）作为纵坐标，组距（等距分组）作为纵坐标
- 频率直方图：频率（数据出现的次数）作为纵坐标，组距（等距分组）作为纵坐标。
频数/总数/组距为纵坐标， - 箱形图：
- 下四分位数：Q1，将所有数据按照从小到大的顺序排序排在第25%位置的数字
- 上四分位数：Q3，将所有数据按照从小到大的顺序排序排在第75%位置的数字
- 四分位距：IQR，等于Q3-Q1，衡量数据离散程度的一个统计量
- 异常点：小于Q1 - 1.5IQR或大于Q3 + 1.5IQR的值
- 上边缘：除异常点以外的数据中的最大值
- 下边缘：除异常点以外的数据中的最大值
- 折线图
- 柱状图：显示一段时间内数据的变化或显示各项之间的比较情况，不同于直方图，柱状图的横坐标通常是离散的
- 饼图
古典概率介绍
随机实验
- 可以在相同的条件下重复进行
- 实验结果不止一个，但是在实验前就知道所有的可能性
- 实验前不知道会出现什么结果
-
事件
一般的，我们称试验 E 的样本空间 S 的某个子集为E的随机事件，简称 事件 。一般用大写字母A,B,C,D……表示。比如掷骰子“所得点数为偶数”“所的点数为1”
- 由一个样本点组成的单点集称为 基本事件 。例子“所得点数为3”
- 某个样本点出现叫做 事件发生 ，例子“掷出6”，称为事件A发生
- 必然事件：每个实验中一定会发生的事件。例子“点数小于7”
不可能事件：每个实验中一定不会发生的事件。例子“点数大于7”
事件之间的关系
包含（
）- 和事件)（
） - 积事件（
） - 差事件（
） - 互斥事件（
） -
事件之间的运算定律
交换律：
；
- 结合律：
；
- 分配律：
；
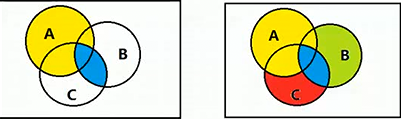
- 德摩根率：
； 
频率和频数
在相同的条件下，重复n次实验，事件A发生的次数称为A发生的频数，
称为事件A发生的频率
终于进入概率
大量的实验证明，当试验的重复次数n逐渐增大时，事件A发生的频率会逐渐稳定于某个常数p。这个P就是事件A发生的概率，用于表示再一次实验中，事件A发生的可能性大小。记事件A的概率为
。
概率需要满足的条件
，有
，即
，有
不可能事件发生的概率为0
，即
，有
俩个事件，若
，则
；
俩个事件，有
（加法公式） # AB表示集合取交集，去掉了交集符号。
若有收获，就点个赞吧
0 人点赞
