Gradient Descent介绍

他不是一个机器学习算法，而是一种基于搜索的最优化方法，是用来最小化一个损失函数，与之相反，梯度上升法是用来最大化一个效用函数的。他俩都是用来最优化目标函数的。在多元线性回归中我们可以用正规方程解，但是很多机器学习的模型是求不到数学解的，所以需要梯度下降法。

下面的平面图表示theta向量中只有一个系数（只有一个特征），即简单线性回归的梯度下降法可视化，每取一个该特征的系数的数值，会得到的损失函数J的不同值。

我们要找到J的最小值，只有当theta所在的点导数为0时，此时该点上这个曲线方程切线的斜率为0，所以这个点在极值点上，就有可能是一个最小值。因为不是所有的函数都有唯一的极值点（导数为0），他可能是当前范围内的局部最优解，所以需要随机化初始点，这个初始点是一个超参数。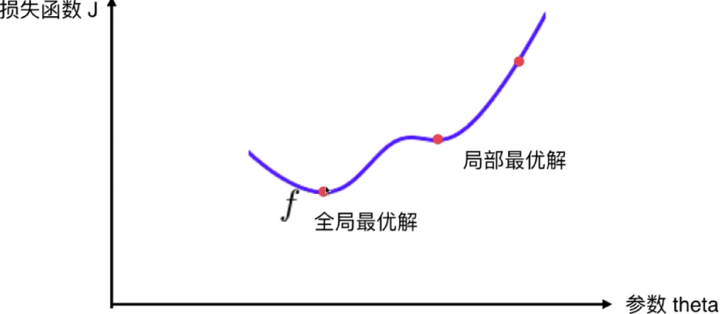，不过线性回归法里的损失函数都具有唯一最优解，因为函数都是规则的，比如上图表示的一元线性回归可视化。

在上图中，导数代表theta单位变化时，J相应的变化，列如theta向左或向右移动都会带来J的变化，或增大或减小。上图的切线斜率为负值，也就是导数为负，theta增加时J减少，theta减小时J增加，说明导数可以代表方向，对应J增大的方向，上图导数为负，所以J增大的方向是X轴的负方向.

对应在上图中，无论随机下降点出现在中轴的左边还是右边
theta值的方程都是theta +（- eta（dJ/dtheta））
左边的时候斜率为负数，J增大的方向为x轴负方向，所以用-eta表示J减小的方向；右边的时候斜率是正数，J增大的方向为x轴的正反向，所以还是用-eta表示J减小方向。

(eta)是什么

称为学习率(learning rate)
的取值影响获得最优解的速度，也就是收敛的速度
收敛就是到达梯度最低点的过程
取值不合适，甚至得不到最优解

是梯度下降法的一个超参数

简单线性回归梯度下降法实现

import numpy as np
import matplotlib.pyplot as plt
plot_x = np.linspace(-1, 6, 141)  # 加上-1,6一共141个点
plot_y = (plot_x - 2.5)**2-1 
plt.plot(plot_x, plot_y)  # 绘制二次曲线
plt.show()  
def dJ(theta):  # 计算当前theta值下损失函数对应的导数
    return 2*(theta-2.5)
def J(theta):
    try:
        return (theta-2.5)**2-1
    """ 防止学习率过大导致theta无限增大，导致J大到计算机无法计算"""
    except:
        return float('inf') 
eta = 0.4
epsilon = 1e-8  # epsilon小的正数
theta = 0.0
theta_history = [theta]
while True:
    gradient = dJ(theta)
    last_theta = theta
    theta = theta - eta * gradient 
    theta_history.append(theta)
    if(abs(J(theta) - J(last_theta))) < epsilon:
        break
print(theta)
print(J(theta))
print(theta_history)
plt.plot(plot_x, J(plot_x))
plt.plot(np.array(theta_history), J(np.array(theta_history)), color='r',marker='+')
plt.show()

为什么下降的长度越来越小？应为虽然eta不变，但是梯度变得越来越小。所以theta向前进的步长也越来越小。导致theta取值上对应的J也下降的慢了。

学习率的设置

当学习率设置成0.8时，
当学习率设置成1.1时，
因为新theta的位置超过了比原来theta的对称轴的点位，导致梯度变得更大了，所以下一次theta的位置梯度更加大，越升越高。

skleran实现随机梯度下降法

from operator import ipow
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import SGDRegressor
boston = load_boston()
X = boston.data
y= boston.target
X = X[y < 50.0]
y = y[y < 50.0]
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)
standardScaler = StandardScaler()
standardScaler.fix(X_train)
X_train_standard = standardScaler.transform(X_train)
X_test_standard = standardScaler.transform(X_test)
sgd_reg = SGDRegressor(n_iter=5)
sgd_reg.fit(X_train_standard,y_train)
sgd_reg.score(X_test_standard,y_test)