并查集（Kruskal算法求最小生成树中判断是否会出现环）

例子来源：天勤论坛数据结构课程http://www.csbiji.com

【背景】https://blog.csdn.net/summer_dew/article/details/81660723
从上一篇中，我们知道，找出最小边之后需要判断该边是不是会构成环

• 构成环：不并入，继续找下一条最小边
• 不构成环：才并入

【并查集】用来判断该边并入后，会不会产生环
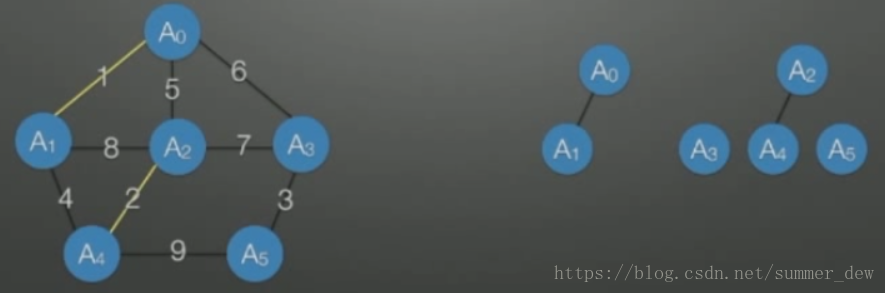
并查集即是右边的散落顶点，但我们这里把它看成一棵棵树
［作用］
1． 可以快速地将两个含有很多元素的集合并为一个
2．方便地判断两个元素是否属于同一个集合

【思路】并入一个最小边时，看两个顶点是否在同一个树中

1. 在同一棵树中，即会产生回路
2. 不在同一棵树中，不会产生回路

【怎么看两个顶点是否在同一个树中呢？】找到顶点A的根rootA，找到顶点B的根rootB—>rootA==rootB即在同一棵树上

【例子】

1. 并查集即是右边的散落顶点，但我们这里把它看成一棵棵树
   
2. 最小边1，边的两个顶点A0,A1不在同一棵树—>并入，并在并查集中将A0、A1构成一棵树
   
3. 最小边2，A2、A4在并查集中不属于同一棵树—>并入，并在并查集中将A2、A4构成一棵树
   
4. 最小边3，A3、A5不在同一棵树—>并入，并在并查集中将A3、A5构成一棵树
5. 最小边4，A1、A4不在同一棵树—>并入，并在并查集中将A0、A1构成一棵树
6. 最小边5，A0、A2在同一棵树（A0所在树的根是A0，A2所在树的根是A0）—>不并入
   
7. 最小边6，A0、A3不在同一棵树—>并入，更新并查集
8. 直到此，所有的结点都在生成树中—>结束，左边黄色的才是生成树，右边的不是生成树，只是帮助我们排除环的工具树