静态查找表

算法 顺序查找法 折半查找法（二分法查找） 分块查找法（索引顺序查找）
查找 查找 - 图1 查找 - 图2 【查找】①确定待查找的元素属于哪一块（折半查找法）；②块内精确查找（顺序查找）
说明 按顺序遍历找元素k 描述折半查找的判定树（二叉排序树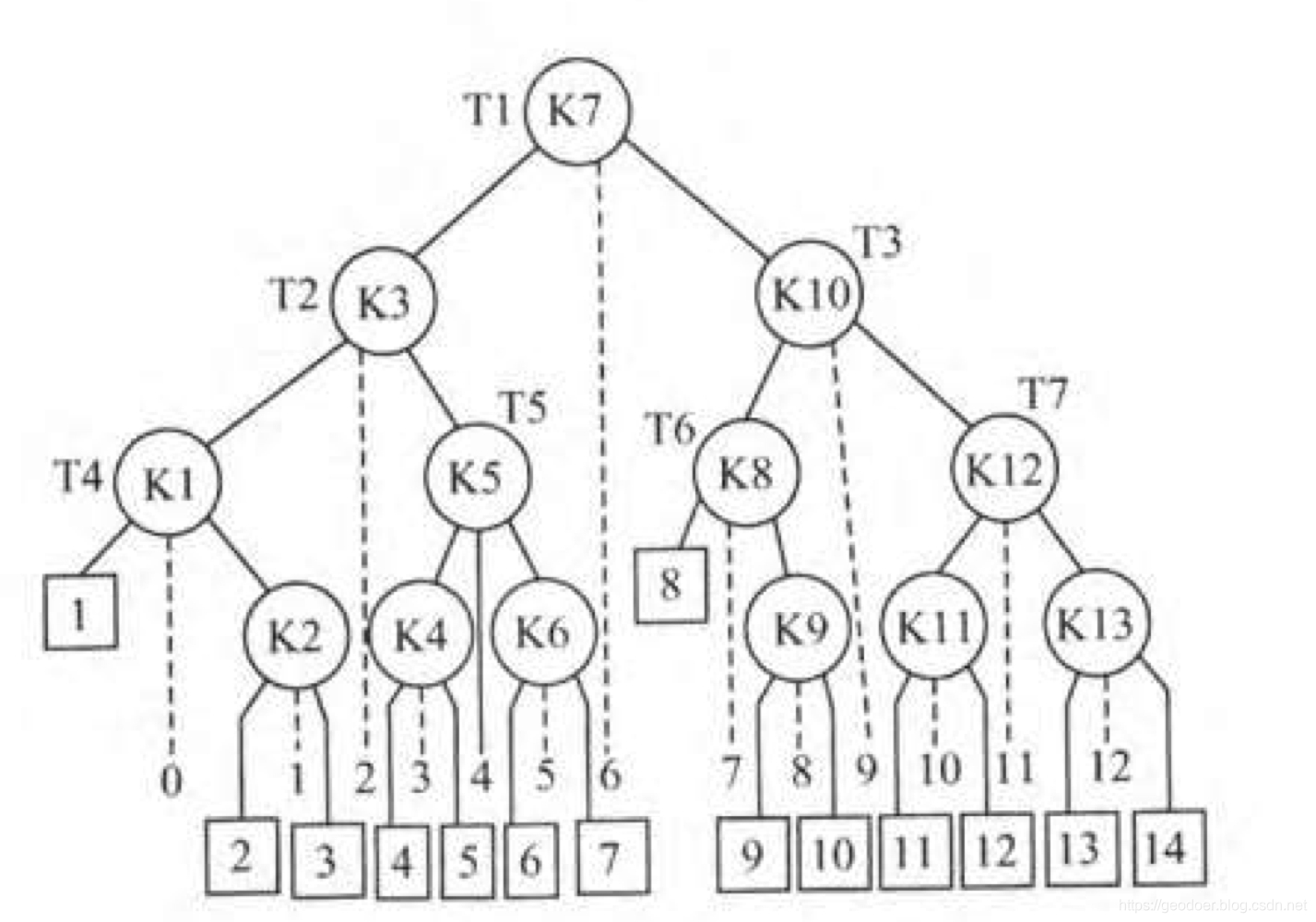）查找 - 图3查找 - 图4 索引表：前一块的最大值<后一块的最小值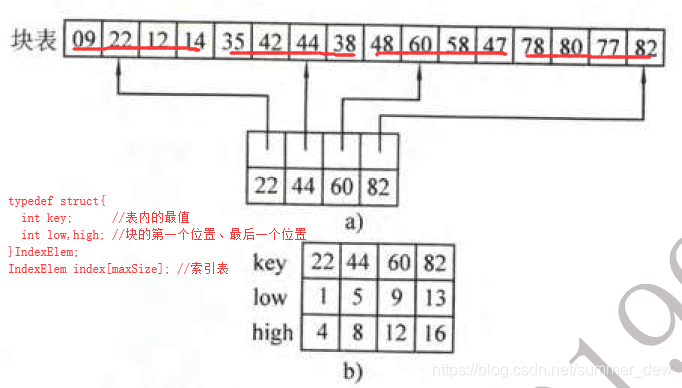
查找 - 图5
成功ASL k在表中，每一个记录的查找长度再求平均查找 - 图6 【一般情况】查找 - 图7-1#card=math&code=ASL%3Dlog_2%28n%2B1%29-1&id=s2VMI)；
【具体例子】求出所有的长度再求平均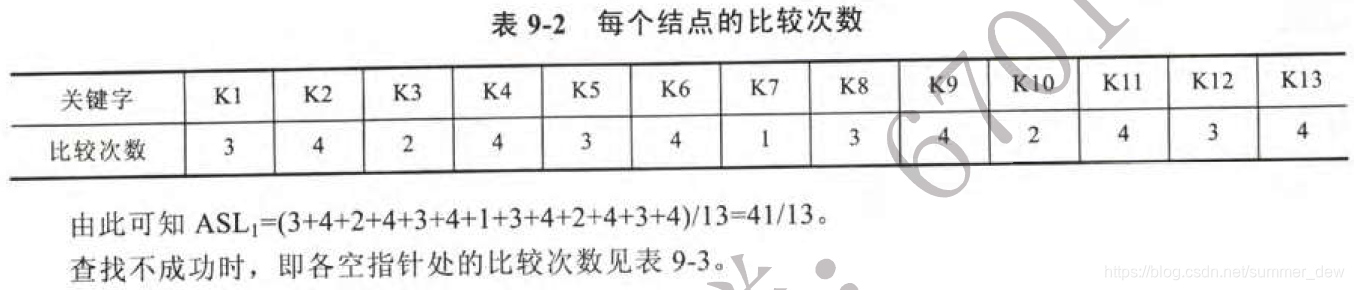查找 - 图8		 折半ASL+顺序查找
失败ASL k在表中没有，全部记录都要遍历一次！
【从前往后】查找 - 图9【从后往前】查找 - 图10		 空指针的比较次数之和再求平均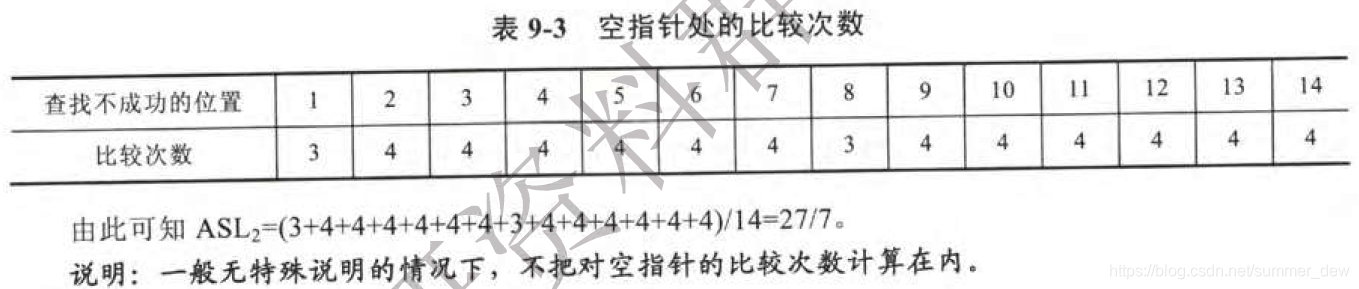
查找 - 图11

动态查找树

说明 示例
二叉排序树 1. 可以为空
2. 左子树<结点<右子树		 查找 - 图12
平衡二叉树 二叉排序树改进
1. 左子树<结点<右子树
2. 每个结点只有一个关键字
3. 一个关键字可以引出2个分支
4. 任何一个结点的左右孩子高度之差≤1		 查找 - 图13
B-树 平衡二叉树的扩展
1. 每个结点最多可以存k个关键字
2. k个关键字可以引出m个分支(m=k+1)
3. 所有叶子结点都在同一层
4. 称为”平衡m叉树“，一般称为“m阶B-树”		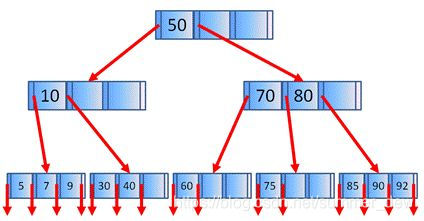 查找 - 图14四阶B树（平衡四叉树）
①每个结点最多可以存3个关键字；②3个关键字可以引出4条分支
B+树 B-树的扩展
1. 非叶子结点只是一个索引，不是真正的记录
2. 把所有记录都放在叶子结点上存储
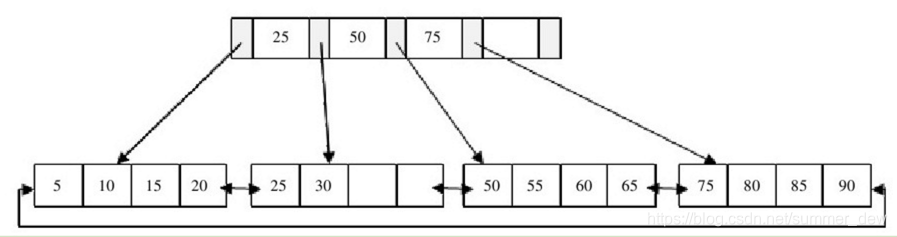3. 用一个链表把叶子结点串起来		 查找 - 图15

二叉排序树

二叉排序树 代码
特点 1. 折半查找法的判定树就是一颗二叉排序树
2. 对二叉排序树进行中序遍历，得到递增有序的序列
存储结构 查找 - 图16
查找 查找 - 图17
插入 查找 - 图18
构造 查找 - 图19
删除 查找 - 图20

平衡二叉树（ASL树）

【平衡因子】平衡因子=左子树高度-右子树高度
【平衡调整】|平衡因子|＞1的结点即失去平衡，要进行平衡调整
【失去平衡的最小子树】是离插入的结点最近，且平衡因子绝对值大于1的结点作为根的子树
【调整步骤】

  1. 插入新结点
  2. 插入后，找出失去平衡的最小子树
  3. 看此状态，属于哪种调整状况
  4. 按调整状况的调整方法调整这棵子树

【调整的四种情况】LL、RR、LR、RL不是描述调整的过程，而是对不平衡状态的描述

名字 调整方法 图例
LL调整在根的左孩子的左孩子上插入结点，导致的不平衡 右单旋转调整：
1. A往下旋转一个位置，变成B的右孩子结点
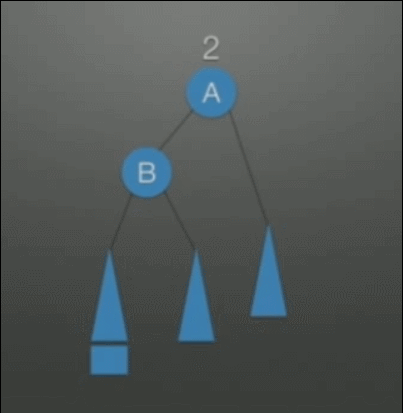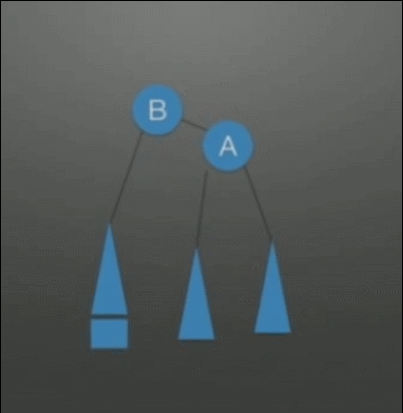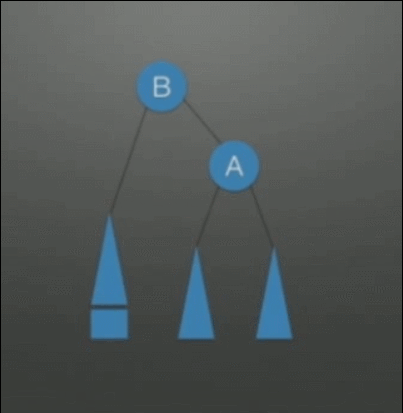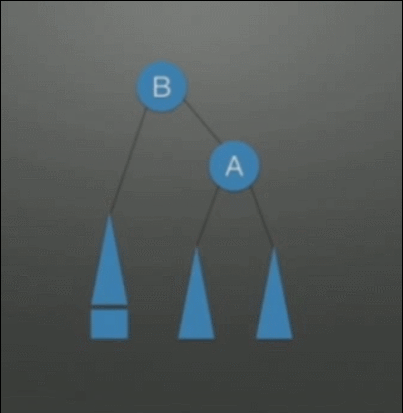2. B的右子树挂在A的左子树上		 查找 - 图21
RR调整在根的右孩子的右孩子上插入了结点，所导致的不平衡（是LL情况的对称情况） 左单旋转调整：
1. A往下旋转一个位置，变成B的左孩子
2. 将B的左孩子挂在A的右孩子上		 查找 - 图22
LR调整
在根结点(A)左孩子(B)的右子树上插入结点，导致不平衡		 先左后右双旋转调整：
1. 把B整体摘下来，变成了RR的情况
2. 对B整体进行RR调整
3. 挂载A结点的空指针上，变成了LL的情况
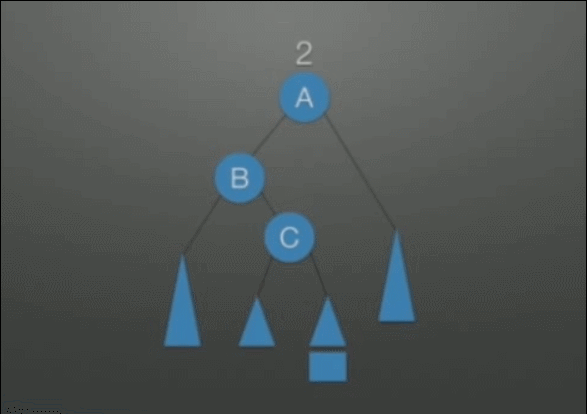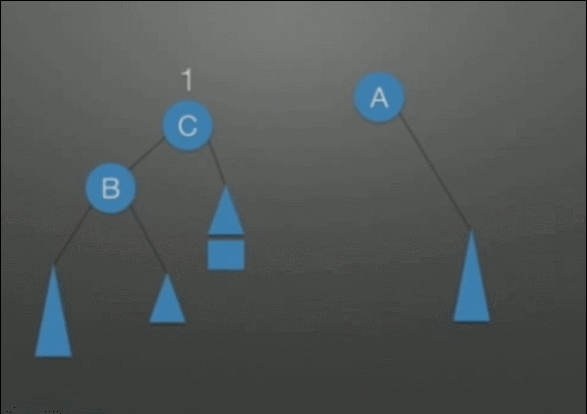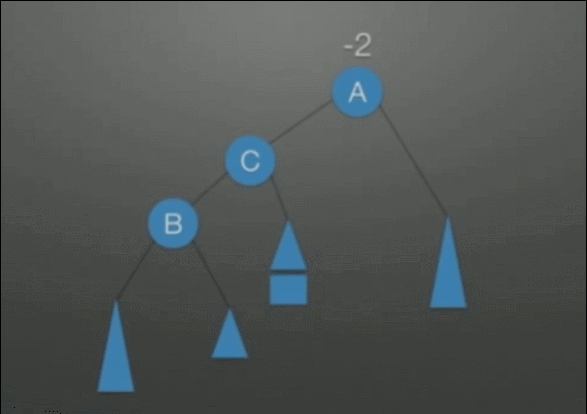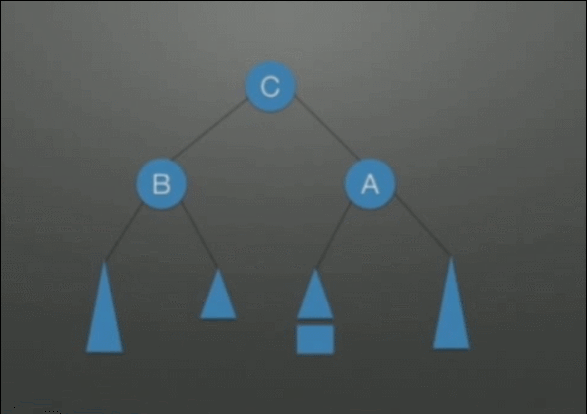4. 对A整体进行LL调整		 查找 - 图23
RL调整
根结点(A)的右孩子的左子树上插入结点，导致的不平衡（是LR调整的对称情况）		 先右后左双旋转调整
1. 把B整体摘下来，变成了LL的情况
2. 对B整体进行LL调整
3. 挂在A结点的空指针上，变成了RR的情况
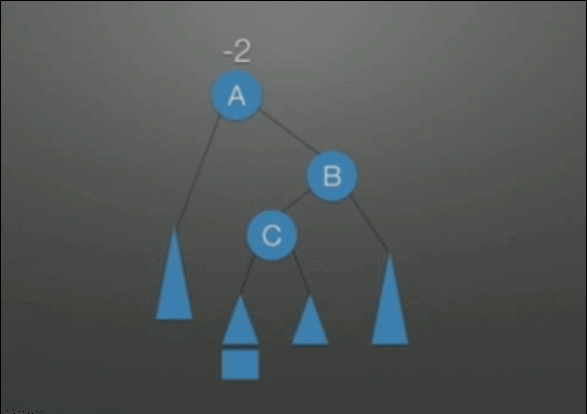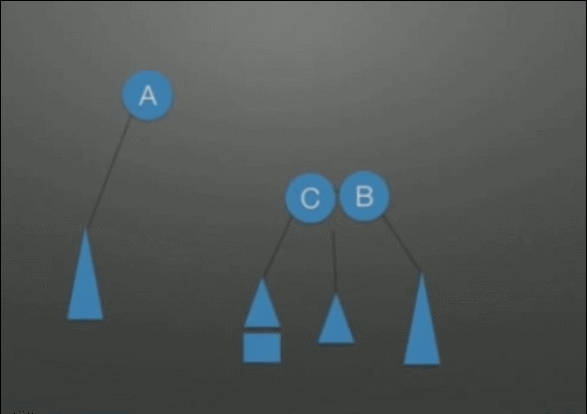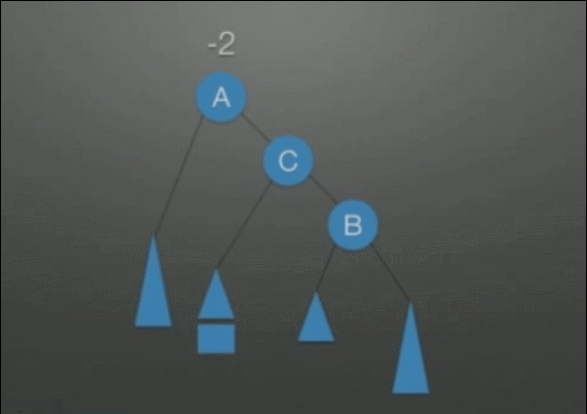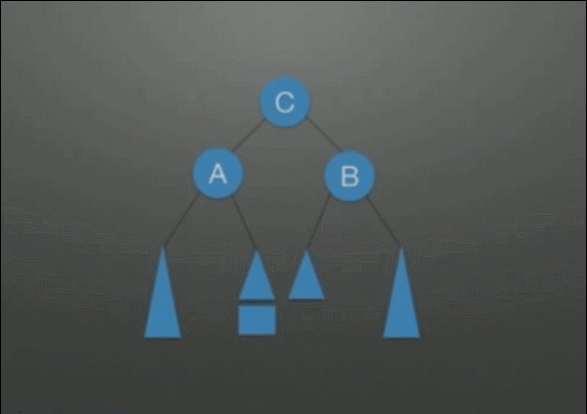4. 对A进行RR调整		 查找 - 图24 
  1. typedef struct BiTNode {
  2.     int data; //关键字
  3.     int bf;    //平衡因子
  4.     struct BiTNode* lchild, *rchild;
  5. }BiTNode, *BiTree;
  6. #define LH +1 //左边高
  7. #define EH 0  //左右高度相等
  8. #define RH -1 //右边高
  9. // 左单旋转调整（RR调整）
  10. void L_Rotate(BiTree *A) {
  11.     BiTree B = (*A)->rchild; //得到B
  12.     B->bf = (*A)->bf = EH;
  13.     (*A)->rchild = B->lchild; //B的左子树给A的右子树
  14.     B->lchild = *A; //A挂到B的左子树上
  15.     *A = B;
  16.     return;
  17. }
  18. // 右单旋转调整（LL调整）
  19. void R_Rotate(BiTree *A) {
  20.     BiTree B = (*A)->lchild;
  21.     B->bf = (*A)->bf = EH;
  22.     (*A)->lchild = B->rchild;
  23.     B->rchild = *A;
  24.     *A = B;
  25.     return;
  26. }
  27. // A的左子树变高了 - 有可能是LL、LR类型
  28. void LeftBalance(BiTree* A) {
  29.     BiTree B = (*A)->lchild; //A的左子树
  31.     switch (B->bf) { //B的平衡因子
  32.     case LH: //B的左边更高 --> LL型
  33.         R_Rotate(A); //对A进行LL调整（即右单旋转调整）
  34.         break;
  35.     case RH: //B的右边高 --> LR型
  36.         L_Rotate(&B);   //对B进行RR调整
  37.         (*A)->lchild = B; //挂在A的左子树上，代替刚才的B
  38.         R_Rotate(A);   //A变成了LL情况，对A进行LL调整
  39.         break;
  40.     }
  41. }
  42. // A的右子树变高了 - 有可能是RL、RR类型
  43. void RightBalance(BiTree *A) {
  44.     BiTree B = (*A)->rchild;
  46.     switch (B->bf) { //B的平衡因子
  47.     case LH: //B的左边更高 --> RL型
  48.         R_Rotate(&B); //对B进行LL调整（即右单旋转调整）
  49.         (*A)->rchild = B; //把新的根挂在A的空节点上
  50.         L_Rotate(A); //对A进行RR调整（即左单旋转调整）
  51.     case RH: //B的右边更高 --> RR型
  52.         L_Rotate(A); //对A进行RR调整（即左单旋转调整）
  53.         break;
  54.     }
  55. }
  56. // 平衡二叉树 - 插入结点
  57. int InsertAVL(BiTree* pT,int data,int *taller) {
  58.     // @taller：该子树有没有变高，0未变高，1长高了
  60.     if( *pT == NULL ) { //找到插入位置
  61.         *pT = (BiTree)malloc(sizeof(BiTNode));   
  62.         (*pT)->bf = EH; //左右高度相等
  63.         (*pT)->rchild = (*pT)->lchild = NULL;
  64.         (*pT)->data = data;
  65.         *taller = 1; //这棵子树长高了
  66.         return 1;
  67.     } else {
  68.         if ( data == (*pT)->data ) { //有相同的结点
  69.             *taller = 0;
  70.             return 0;
  71.         } else if ( data < (*pT)->data ) {
  72.             // 往左子树搜索
  73.             if ( InsertAVL( &(*pT)->lchild, data, taller) ) {
  74.                 // 在左子树插入成功
  75.                 if (*taller) {
  76.                     // 左子树长高了
  77.                     switch ( (*pT)->bf ) { //没插入前pT的平衡因子是
  78.                     case LH: //没有插入前，pT左边就高出了1
  79.                         LeftBalance(pT); //插入后左边不平衡-->调整
  80.                         *taller = 0;     //这棵没有变高，已经被处理掉了
  81.                         break;
  82.                     case EH: //没有插入前，pT两边平衡
  83.                         (*pT)->bf = LH; //插入后，左边高出了1
  84.                         *taller = 1;    //这棵子树变高了
  85.                         break;
  86.                     case RH: //没有插入前，pT右边高
  87.                         (*pT)->bf = EH; //插入后，左右平衡
  88.                         *taller = 0;    //这棵子树没有变高
  89.                         break;
  90.                     } //switch
  91.                 } // if
  92.                 return 1; //插入成功
  93.             } //if 
  94.         } else if ( data > (*pT)->data ) {
  95.             // 往右子树搜索
  96.             if ( InsertAVL( &(*pT)->rchild, data, taller) ) {
  97.                 // 在右子树插入成功
  98.                 if (*taller) {
  99.                     // 右子树长高了
  100.                     switch ( (*pT)->bf ) { //没插入前pT的平衡因子是
  101.                     case LH: //没插入前，pT的左子树高出了1
  102.                         (*pT)->bf = EH; //插入后，左右平衡
  103.                         *taller = 0;    //这棵子树没有变高
  104.                         break;
  105.                     case EH: //没插入前，pT两边平衡
  106.                         (*pT)->bf = RH; //插入后，右边高
  107.                         *taller = 1;    //这棵子树长高了
  108.                         break;
  109.                     case  RH: //没插入前，pT的右子树更高
  110.                         RightBalance(pT); //插入后，右子树不平衡
  111.                         *taller = 0;
  112.                         break;
  113.                     } //switch
  114.                 } //if
  115.             } //if
  116.             return 0;
  117.         } // else if
  118.     }
  119.     return 0; //插入失败
  120. }

B-树

【名称】B-树叫“B树”，中间的”-“不是减号，是一个横杆，而B+树，确实就叫“B加树”，中间是“+”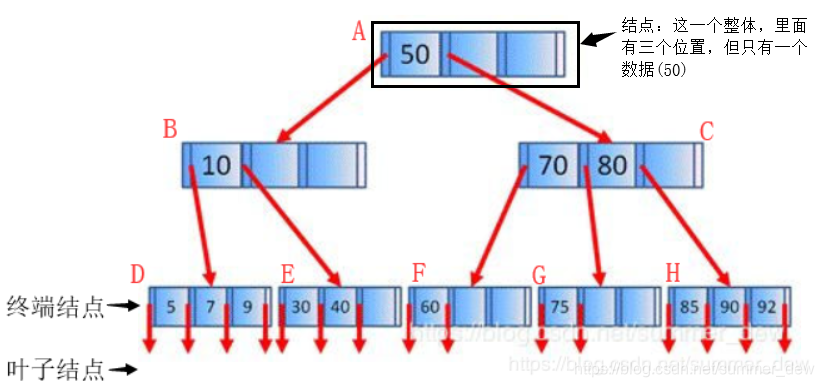
查找 - 图25

m阶B-树（举例：上图） 特点
阶数m（四阶m=4） 【阶数是一定的】一个结点可以坐多个人是定制座位的时候就决定的
1. 一个结点有m-1个位置（可以放3个数据），但结点内数据可以不装满（ABCEFG没装满）
2. 一个结点最多有m颗子树（DH有最多子树，4个）
3. 所有数据不重复
终端结点 有数据的最下层（DEFGH），叶子结点的上一层
叶子结点 叶子结点是终端结点（DEFGH）的下一层，整棵树的是最下一层
结点的数据个数 有n个分支的结点，有n-1个关键字，并且关键字有序排列
1. 【根结点】1≤数据个数≤m-1
2. 【其他结点】⌈m/2⌉-1≤数据个数≤m-1
结点的分支个数 结点的分支个数=结点的数据个数+1
【根结点的分支】①若根结点没有数据：分支=0；②有数据：2≤分支≤m
【非叶子结点】⌈m/2⌉≤非叶子结点的分支≤m（2≤非叶分支(ABC)≤4）
【叶子结点】无分支
高度 两种说法：①3层：不包括叶子结点那一层；②4层：包括叶子结点那一层
整棵树的结点总数 8个（非叶子结点ABCDEFGH）+15（叶子结点的个数）=23

【B-树的操作】查询和二叉排序树相似

B-树插入

举例：五阶B-树 说明
结点的关键字≥m 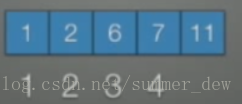查找 - 图26
把位置k=⌈m/2⌉的结点提取出来 查找 - 图27
把k左右边的关键字拆分成两个 查找 - 图28

【完整例子】四阶B-树

查找 - 图29

B-树删除

#define m 5 //阶数
e=删除的关键字
A=e所在结点
min_node_num = m/2-1     //每个普通结点至少要有1个数据
max_node_num = m-1        //每个普通结点最多只有4个数据

if A 是 终端结点:
    if 删除后的关键字个数 ≥ min_node_num：//例子①：删除8
        直接删除e
    else if 删除后的关键字个数 ＜ min_node_num:
        if 两个兄弟中有一个兄弟的关键字个数 ＞ min_node_num： //例子②：删除15
            向其中一个兄弟结点借关键字（父亲下来，兄弟结点上去，自己删除）
        else if 两个兄弟结点关键字个数都 ≤ min_node_num： //例子③：删除4
            结点合并（父亲结点、兄弟结点、自己三者合并）
            while 合并后，父亲结点的个数 ＜min_node_num： //循环处理到父亲结点的个数也满足要求
                if 父亲结点不在了: break //父亲结点是根结点 
                继续结点合并（父亲结点、兄弟结点、自己三者合并）
else if A 不是 终端结点： //例子④：删除16
    用该结点的前驱或后继代替它 //用17代替它
例子 操作 图
五阶B-树 初始状态 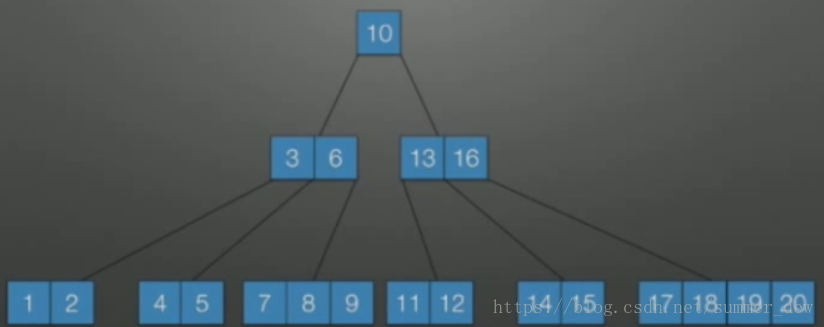查找 - 图30
删除8 删除之后，结点个数还是≥2，依旧满足条件，直接删除 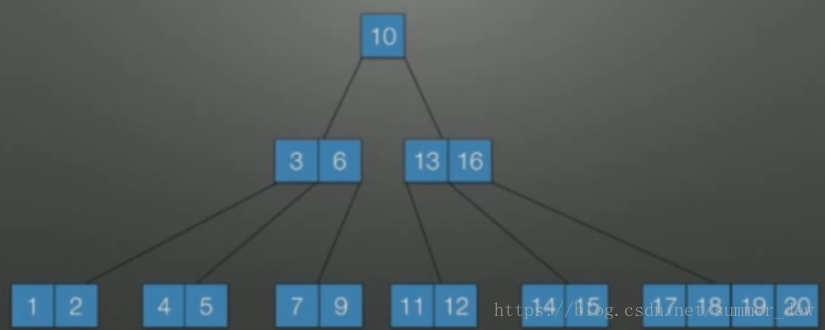查找 - 图31
删除16 用16的后继17代替它 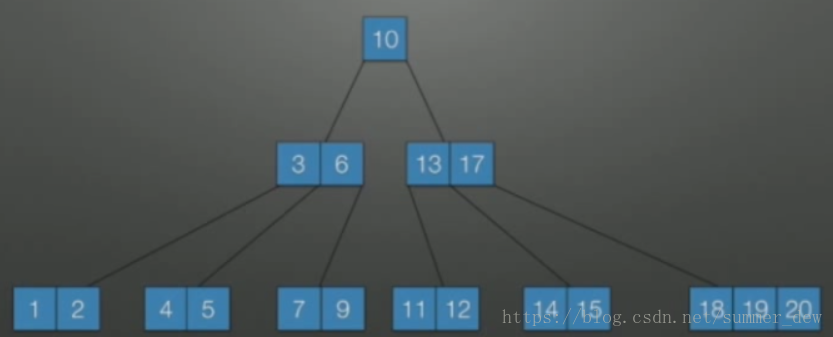查找 - 图32
删除15 1. 删除之后，15所在结点的数据＜2个（只剩下14），不满足条件，向兄弟结点借一下
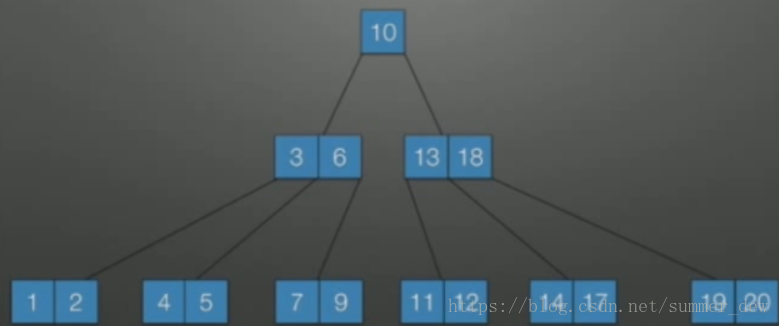2. 17（父亲）下来，18（兄弟）上去，删除15（自己删除）		 查找 - 图33
删除4 4删除后，4所在结点的关键字个数＜2，不满足条件。但是兄弟结点的个数又少，借不了 —> 合并 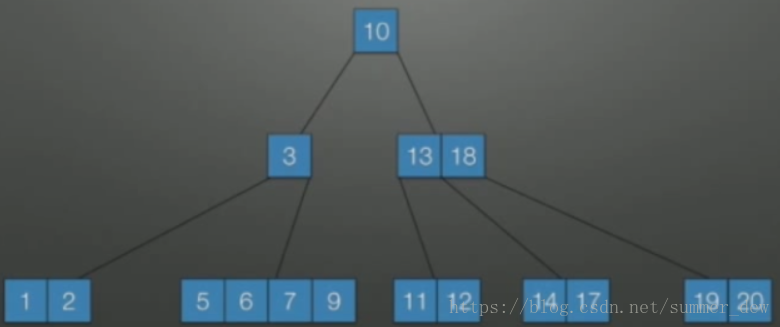查找 - 图34
合并之后，父亲结点的关键字＜2，继续合并，直到父亲的结点的关键字符合要求 查找 - 图35

B+树

B-树 B+树
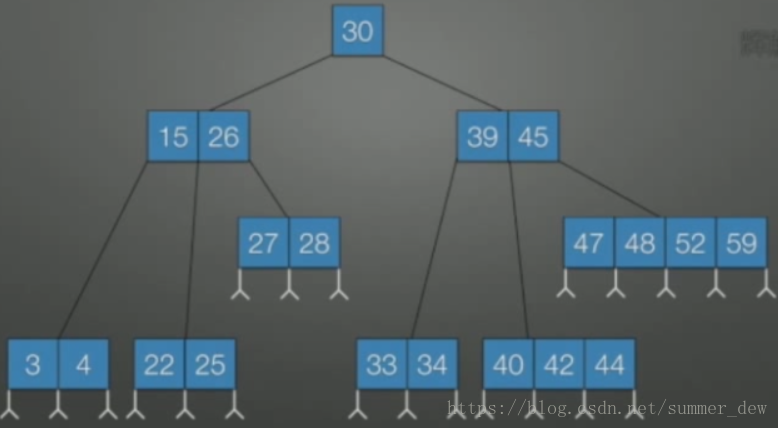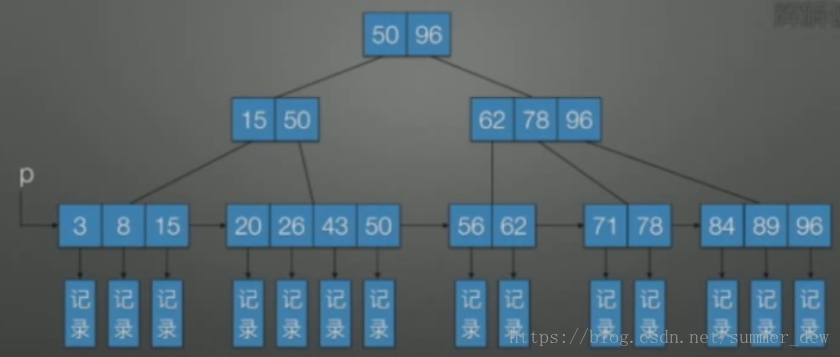示例 查找 - 图36 查找 - 图37
分支个数 具有n个关键字的结点含有n+1个分支 具有n个关键字的结点含有n个分支
关键字个数n 普通结点：⌈m/2⌉-1≤n≤m-1
根结点：1≤n≤m-1		 普通结点：⌈m/2⌉≤n≤m
根结点：2≤n≤m
叶子结点 叶子结点是空指针（白色部分），但实际应用中也可能挂记录 叶子结点包含信息，并且包含了全部关键字，叶子结点引出的指针指向记录
非叶子结点 每个非叶子结点都有记录 只起到了一个索引作用，真正记录还在最下层（叶子结点）中
其他特征 有一个指针p指向关键字最小的叶子结点，把所有的叶子结点连成一个线性链表

其他资料

  1. 图解B-树，B+树