AOE网
【有向无环图】活动在边上的网(Vctivity On edge network),常用来模拟施工流图,进而管理工程的工期
【例子】此图来源于《数据结构高分笔记》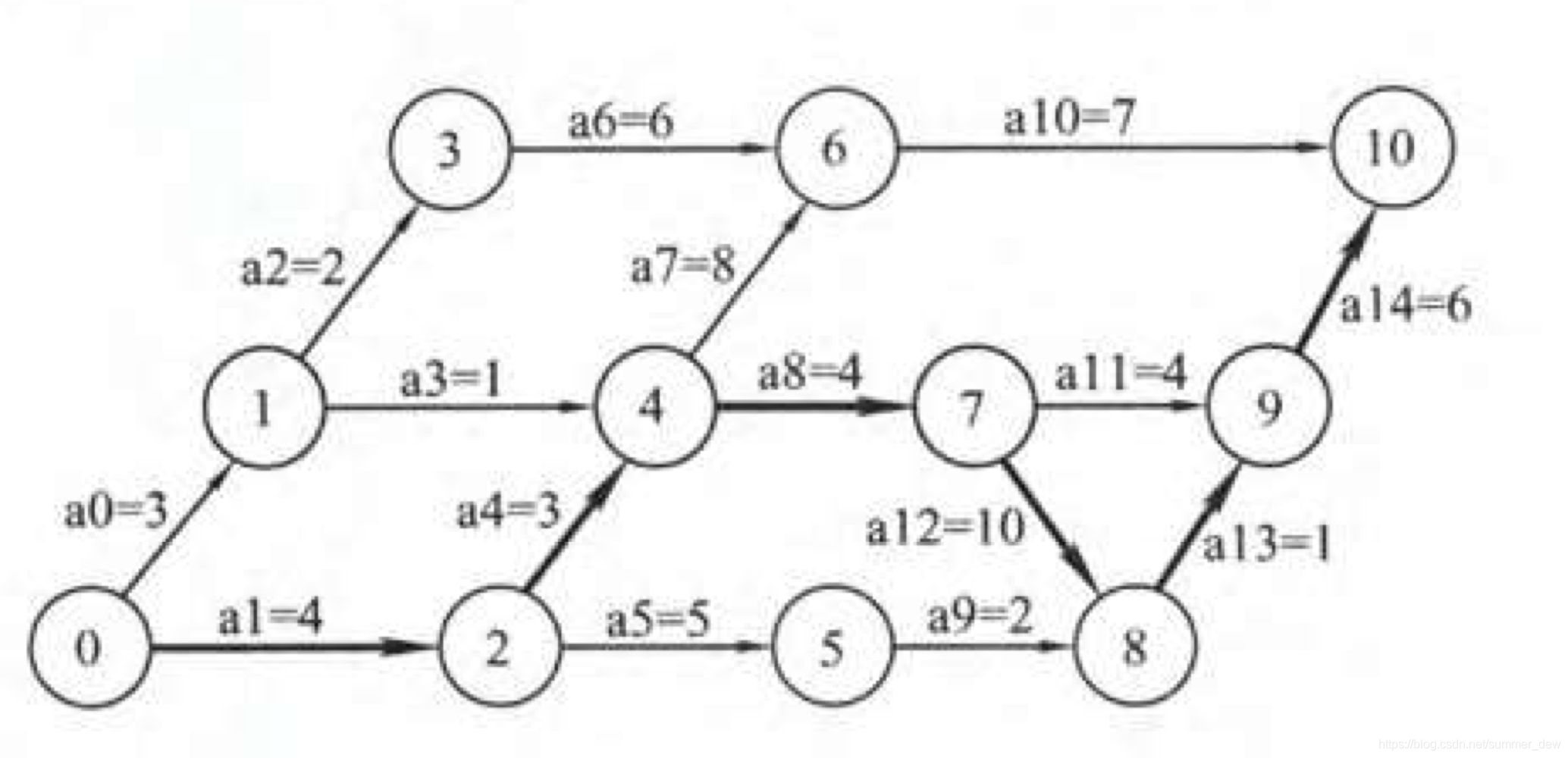
| 概念 | 说明 | 举例 |
|---|---|---|
| 边 | 边表示活动,且有权值,权值代表活动的持续时间 | 【边a4】代表活动,权重3,表示该活动要持续3天 |
| 顶点 | 顶点代表事件,事件是图中新活动开始、旧活动结束的标志 | 【顶点1】代表事件,是活动a2、a3的开始,是活动a0的结束 |
| 源点 | 入度为0的顶点,即工程的开始 | 顶点0 |
| 汇点 | 出度为0的顶点,即工程的结束 | 顶点10 |
AOE的应用(AOE的相关概念)
AOE常用来模拟施工流图,进而管理工程的工期,例如在工程中哪些工作要先做;为了控制工期,哪个工作在哪个时间点必须开始
【先来理解一下“最早”、“最迟”、“关键”】工程:考数学。工期:8:30-11:30
- 【最早发生时间】8:30开始考试,你可以先睡一觉,再起来写;但是你最早开始答题的时间也只能是8:30
- 【最迟发生时间】11:30要交卷,你预估最后一大题要花30min时间,那么你开始做最后一大题的最迟时间是11:00,要不就来不及咯
- 【剩余时间】你预留了30min给最后一大题,那么11:00开始做最后一题做就好了;结果你太聪明,9:00就做到了最后一题;这时有2个小时的空余时间,即是剩余时间,它反应的也是一种松弛度
- 【关键活动或关键事件】剩余时间为0的事件或活动就称之为“关键”,因为做完它前面的事情,这件事情就必须要开始,没有耽搁的余地
| 概念 | 解释 | 举例 |
| —- | —- | —- |
| | |
 |
| 事件k的最早发生时间ve(k) | ve即vertex earliest
|
| 事件k的最早发生时间ve(k) | ve即vertex earliest
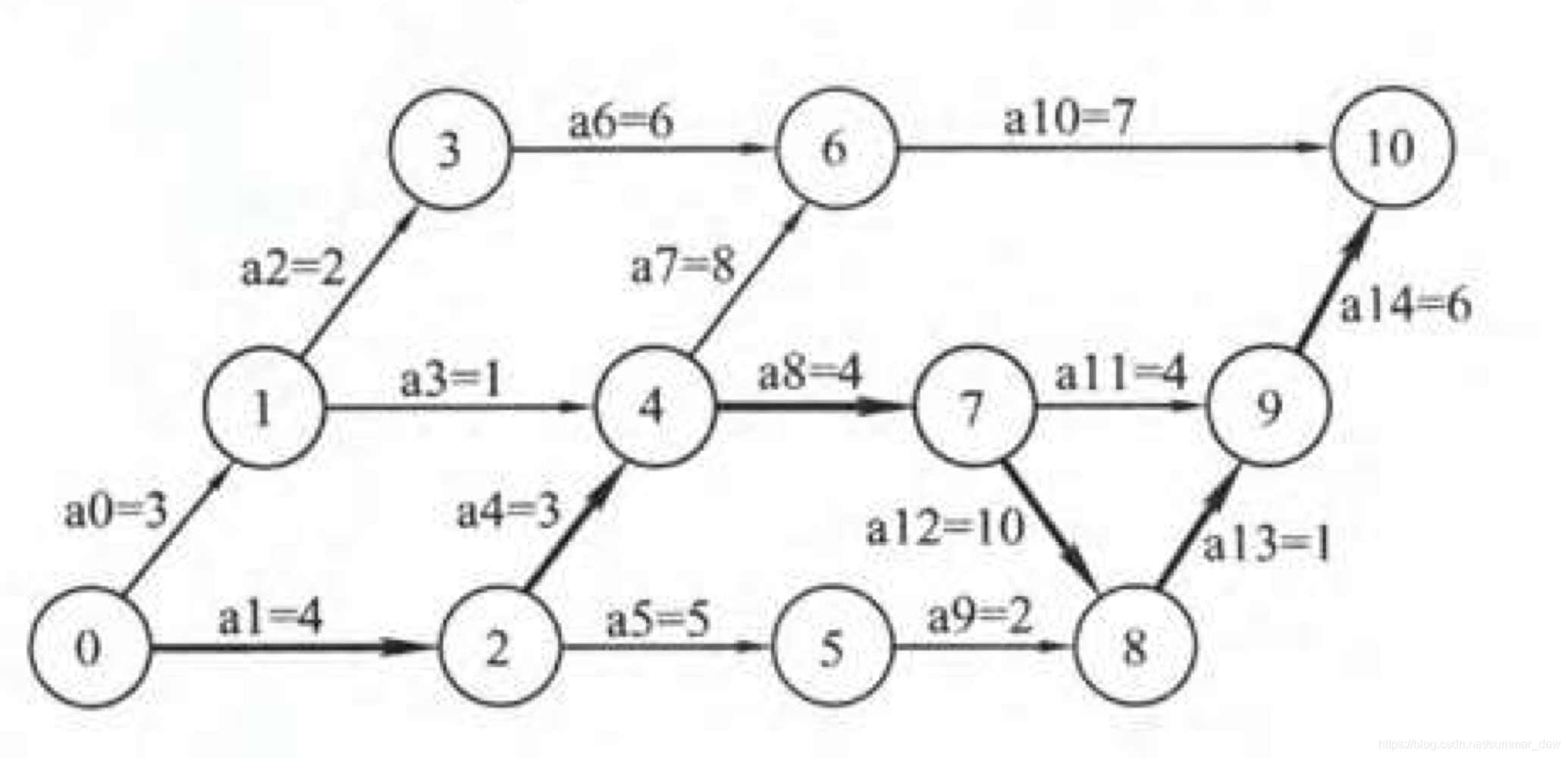
【图中表现为】源点到顶点k的最长路径 | 若事件4要发生,事件4的上游0、1、2都要先发生
【即】事件4的最早发生时间ve(4)=0到4的最长路径=7 | | 活动z的最早发生时间ee(z) | ee即edges earliest
ve是说顶点的最早发生时间,ee是说边的最早发生时间 | 【解释】a7、a8的最早发生时间,即是事件4的最早发生时间,如ee(a7)=ee(a8)=ve(4)=7
【算法】ee(z)=ve(k)
顶点k是边z的头顶点
【例】边a3的头顶点是1:ee(a3)=ve(1)=3| | 关键路径 | 从源点到汇点,图中最长的路径称为关键路径
【现实意义】整个工期所完成的最短时间 | 【即0->10的最长路径】a1->a4->a8->a12->a13->a14
【关键路径的时间即为此工程完成的最短时间】a1+a4+a8+a12+a13+a14=28| | 关键活动 | 关键路径上的活动
【现实意义】若想要最短时间完成这项工程,这些活动的上游完成后,不能休息,要立刻开始! |a1、a4、a8、a12、a13、a14| | 事件k的最迟发生时间vl(k) | vl即vertex latest
在不推迟工期的前提下,事件k最迟发生时间 | 1. 根据关键路径得到工程结束的最短时间为28天
2. 事件7距离完成需要17天(7-10有两条路,取时间大的:①7->9->10的时间要10天,②7->8->9->10要17天)
3. 那么,事件7最迟要在第11天开始!不然28天就完不成了!
【即】vl(7)=28-17=11| | 活动的最迟发生时间el(z) | el即edges latest
在不推迟工期的前提下,活动z最迟发生的时间 | 【解释】a8的最迟发生时间=vl(7)-a8的权重=vl(7)-4=7
【算法】el(z)=vl(k)-z
顶点k是边z的尾顶点
【例】边a14的尾顶点是10:el(a14)=vl(10)-a14=28-6=22|
原理:求关键活动和关键路径
【要注意区分】ve、vl与ee、el的区别
- ve、vl针对的是顶点而言,顶点代表的是事件
- ee、el针对的是边而言,边代表的是活动
求ve、vl(顶点)
| 概念 | 说明 | 求法 |
|---|---|---|
| ve(vertex earliest) | 顶点的最早发生时间,即事件的最早发生时间 | ①求出拓扑有序序列;②源点的ve=0;③按拓扑序列从头到尾计算 ve(k)={ve(j)+<j,k>}的最大值(j为k的上一个结点) |
|
| vl(vertex latest) | 顶点的最迟发生时间,即事件的最迟发生时间 | ①求出逆拓扑有序序列;②汇点的vl=ve=28
;③按逆拓扑序列从尾到头计算vl={vl(j)-<k,j>}的最小值
(j为k的下一个结点) |
【拓扑有序序列】0 1 2 3 4 5 6 7 8 9 10,按此顺序求ve
【逆拓扑有序序列】10 9 6 8 5 7 3 4 1 2 0,按此顺序求vl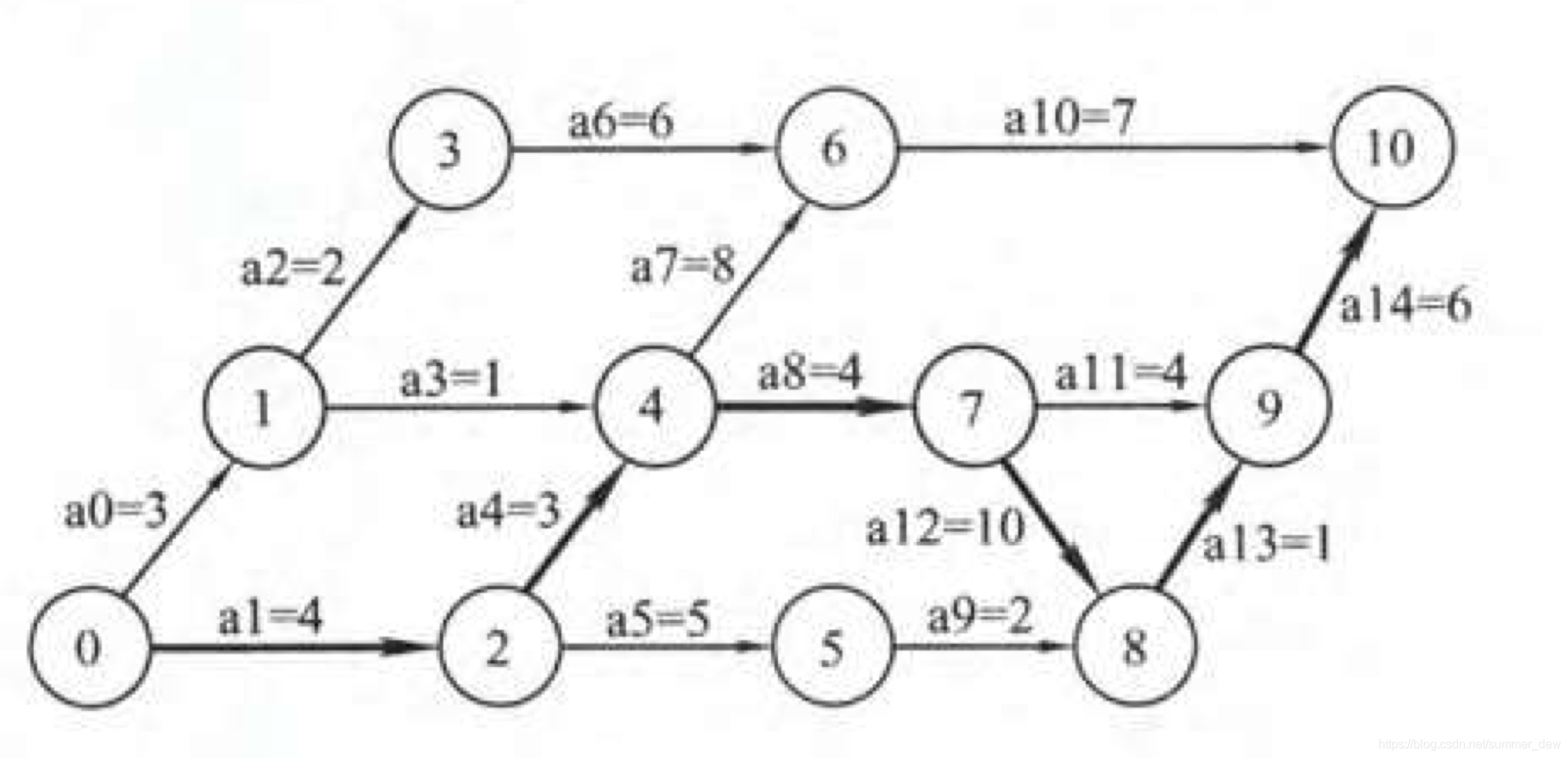
| 顶点 | ve(顶点) | vl(顶点) |
|---|---|---|
| 0 | 0 | min{v1(1)-a0, vl(2)-a1}=0 |
| 1 | ve(0)+a0=3 | min{vl(3)-a2, vl(4)-a3}=6 |
| 2 | ve(0)+a1=4 | min{vl(5)-a5, vl(4)-a4}=4 |
| 3 | v(1)+a2=5 | vl(6)-a6=15 |
| 4 | 两条路:①ve(1)+a3=4;②ve(2)+a4=7 取最大值:ve(4)=7 |
min{vl(6)-a7, vl(7)-a8}=7 |
| 5 | ve(2)+a5=9 | vl(8)-a9=19 |
| 6 | 两条路:①ve(3)+a6=11;②ve(4)+a7=15; 取最大值:ve(6)=15 |
vl(10)-a10=21 |
| 7 | ve(4)+a8=7+4=11 | 两条路:①vl(9)-a11=18;②vl(8)-a12=11 取最小值:vl(8)=11 |
| 8 | max{ve(7)+a12, ve(5)+a9}=21 | vl(9)-a13=21 |
| 9 | max{ve(7)+a11, ve(8)+a13}=22 | vl(10)-a14=22 |
| 10 | max{ve(6)+a10, ve(9)+a14}=28 | 28 |
求ee、el(边)
| 概念 | 说明 | 求法 | 举例 |
|---|---|---|---|
| ee(edges earliest) | 边的最早发生时间,即活动的最早发生时间 | ①从前往后,遍历顶点;②记下顶点引出的边z;③ee(z)就等于顶点的ve | ①看顶点0;②顶点0引出了边a0、a1;③ee(a0)=ee(a1)=ve(0)=0;④看一下个顶点,以此类推 |
| el(edges latest) | 边的最迟发生时间,即活动的最迟发生时间 | ①从后往前,遍历边,看此边的尾顶点k;②边的el=ve(k)-边的权重 | ①看边a14,a14的尾顶点是10;②el(a14)=ve(10)-a14=28-6=22;③继续看下一个边a13,以此类推 |
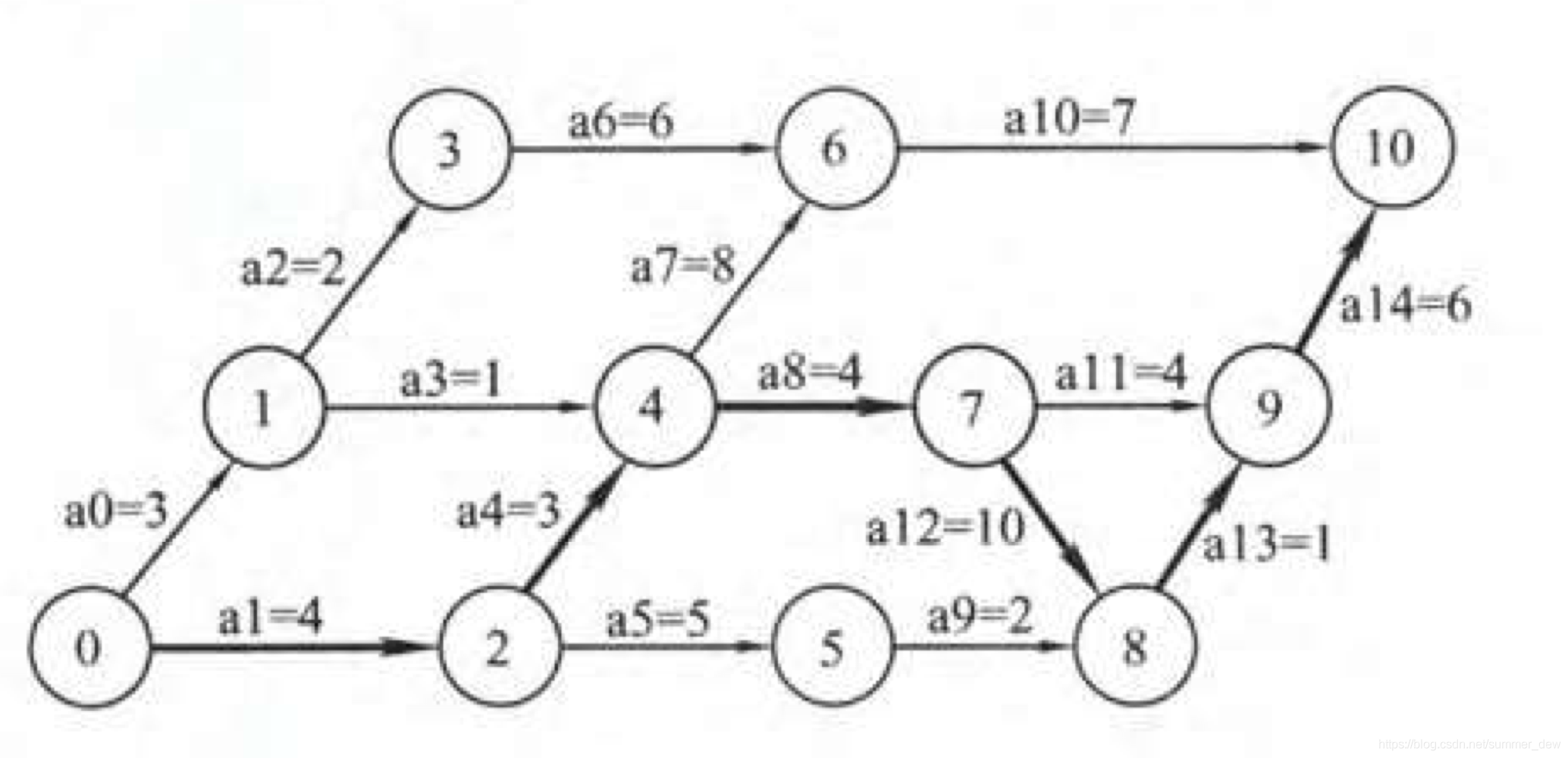
| 例子 | ee和el |
|---|---|
 |
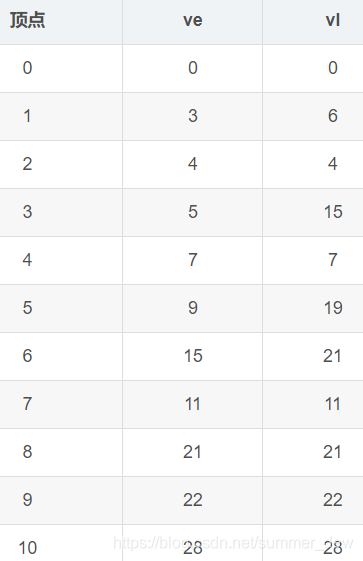 |
| 边 | ee(边) | el(边) |
|---|---|---|
| a0 | 0 | 3 |
| a1 | 0 | 0 |
| a2 | 3 | 13 |
| a3 | 3 | 6 |
| a4 | 4 | 4 |
| a5 | 4 | 14 |
| a6 | 5 | 15 |
| a7 | 7 | 13 |
| a8 | 7 | 7 |
| a9 | 9 | 19 |
| a10 | 15 | 21 |
| a11 | 11 | 18 |
| a12 | 11 | 11 |
| a13 | 21 | 21 |
| a14 | 22 | 22 |
求关键路径,关键活动
| 关键活动 | 关键路径 | 整个工程完成的最短时间 | |
|---|---|---|---|
| 说明 | ee=el的活动即为关键活动 | 关键活动构成的路径 | 关键活动的权重之和 |
| 解释 | ee=el代表活动不能够推迟的,若该活动推迟了,工程就不能在工期内完成 | 关键路径即图中的最长路径 | 图中的所有活动都要完成,中间不停歇,完成整个工程的最短时间就是图中最长的路径,即关键路径 |
| 例子 | a1 a4 a8 a12 a13 a14 |
0->2->4->7->8->9->10 |
整个工程完成的最短时间:a1+a4+a8+a12+a13+a14=28 |
手算举例
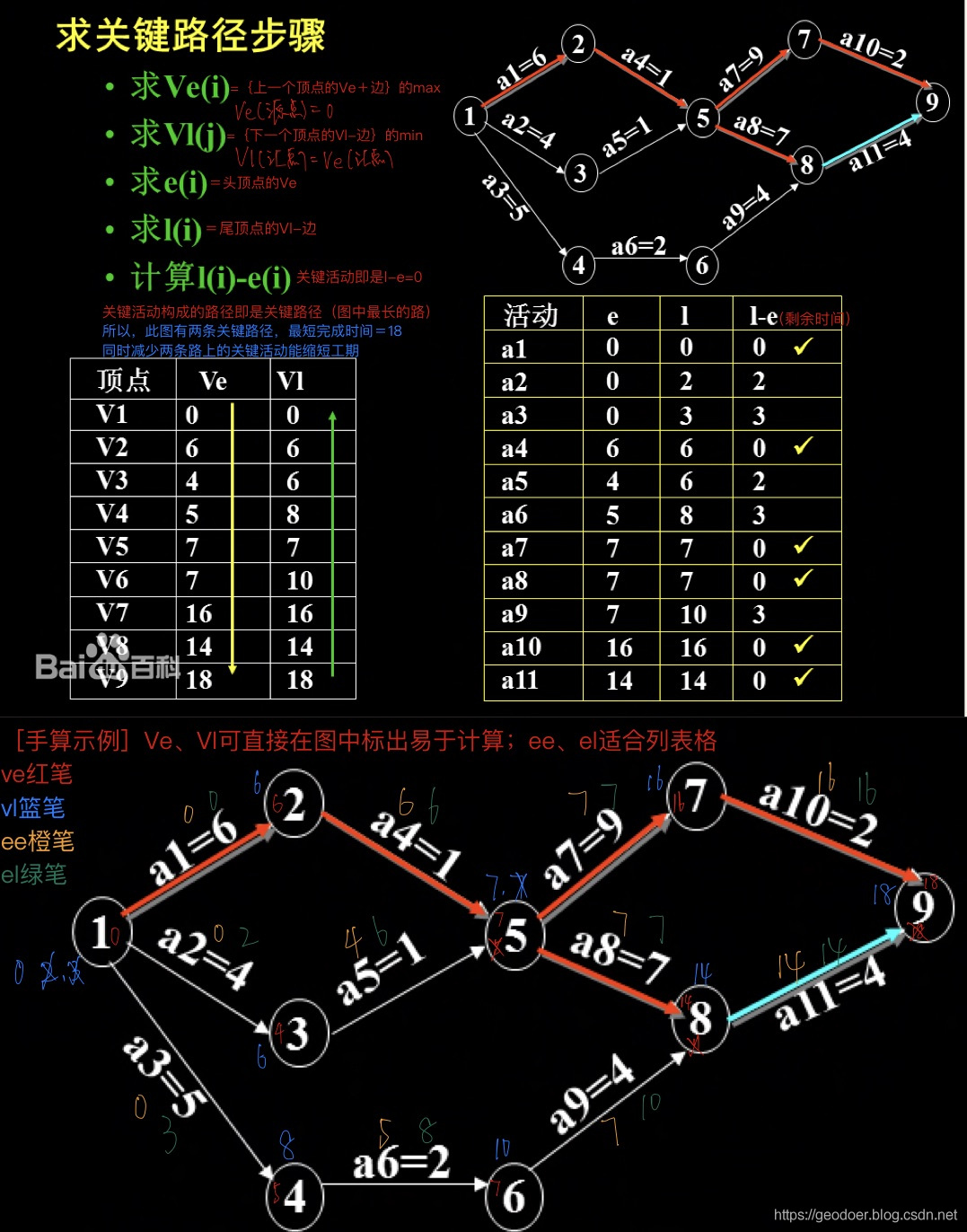
C语言实现
【方法一】关键路径即是图中最长的一条(可修改Dijkstra、Floyd算法求)
1.用拓扑排序获得图的源点v和汇点w
2.计算v到w之间的最长路径
【方法二】求ve、vl、ee和el的算法,时间复杂度O(n+e)
typedef struct ArcNode{int adjvext;int w;struct ArcNode *nextarc;}ArcNode;typedef struct{char data;int cnt; //记录该结点的入度ArcNode *firstarc;}VNode;typedef struct{VNode vers[MAXSIZE];int vernum, arcnum;}ALGraph;// 计算每个结点的入度void CntVNodeInDegree(ALGraph &G) {for (int v=0; v<G.vernum; v++) {for (ArcNode *p=G.vers[v].firstarc; p; p=p->next) {int w = p->adjvex; //边v->wG.vers[w].cnt++; //w的入度+1}}};// 拓扑排序:order[]为拓扑有序序列,返回1表示图为有向无环图int TopSort(ALGraph &G, int order[]) {int stack[MAXSIZE], top=-1; //存放入度为0的顶点int v,w,n;// 将图中入度为0的顶点入栈for (i=0; i<G.vernum; ++i)if (G.vers[i].cnt==0) stack[++top] = i;n=0; //已删除n个顶点while(top!=-1) { //还有入度为0的顶点v = stack[top—-]; //出栈//删除此顶点order[n] = v; n++;for (ArcNode *p=G.vers[v].firstarc; p; p=p->next) {w = p->adjvex;—-(G.vers[w].cnt);if (G.vers[w].cnt==0) stack[++top]=w;}}if (n==G.vernum) return 1;else return 0;}// 关键路径int CriticalPath(ALGraph &G, int **map) {// map[G.vernum][G.vernum]为G的邻接矩阵;map[v][w]=1表示v->w为关键活动。初始值为INF,表示不是关键活动int topo[G.vernum];int ve[G.vernum] = {0}, vl[G.vernum] = {0};int v, w;ArcNode *p;// 拓扑排序:检查是否为有向无环图,并获得拓扑序列存到topo[]中if (TopSort(G, topo)==0 ) return 0;// 计算每个顶点的ve:ve[]初始值为0,ve[w]=Max{ve[v] + vw的边权重}for (i=0; i<G.vernum; i++) ve[i]=0; //ve[]初始值为0for (i=0; i<G.vernum; i++) { //遍历拓扑有序序列v = topo[i]; //得到拓扑有序序列的顶点// 计算它的下一个顶点:v->wfor (p=G.vers[v].firstarc; p; p=p->next) {w = p->adjvex; //它的邻边v->wif (ve[w] < ve[v]+p->w) //ve(尾) ve(头)+边。取最大值ve[w] = ve[v]+p->w; //ve(尾)=ve(头)+边}}// 计算每个顶点的vl:vl[]初始值为ve[汇点],vl[w]=min{vl[v] - vw边的权重}v = topo[G.vernum-1]; //汇点for (i=0; i<G.vernum; ++i) vl[i]=ve[v]; //vl[]初始值为ve[汇点]for (i=G.vernum-1; i>=0; i—-) { //从后往前遍历拓扑有序序列v = topo[i]; //拓扑有序序列的顶点// 计算它的下一个顶点:v->wfor (p=G.vers[v].firstarc; p; p=p->next) {w = p->adjvex; //它的邻边v->wif (vl[v] > vl[w]-p->w) //vl(头) vl(尾)-边。取最小值vl[v] = vl[w]-p->w; //vl(头)=vl(尾)-边}}// 求关键活动int ee, el; //当前活动的ee、elfor (i=G.vernum-1; i>=0; i—-) { //从右往左遍历拓扑有序序列v = topo[i];for (p=G.vers[v].firstarc; p; p=p->nextarc) { //遍历该顶点的边w = p->adjvex; //它的邻边v->wee = ve[v]; //ee(vw)=ve(v)el = vl[w]-p->w; //el(vw)=vl(尾)-边if (ee==el) { //为关键活动printf(“(%c->%c)\t”, G.vers[v].data, G.vers[w].data);map[v][w] = 1; //v-w边为关键活动}}}return 1;}void PrintAllCriticalPath(ALGraph &G, int **map, int start, int end) {static char path[MAXSIZE] = {‘\0’};static int index = 0;// 关键路径不只一条,打印出所有的关键路径path[index++] = G.vers[start].data;if (start==end) {path[index] = ‘\0’;printf(“%s\n”, path);} else {for (ArcNode *p=G.vers[start].firstarc; p; p=p->nextarc) {int w = p->adjvex;if (map[start][w]==1) {PrintAllCriticalPath(G, map, w, end);}}}index—-;}

