3.2 有向图的强连通分量-原理：https://blog.csdn.net/summer_dew/article/details/81666877

Kosaraju算法可以在线性时间和线性空间内找出一个图的强分量

举例

举个例子就很容易理解该算法了

【图G】求图G的强连通分量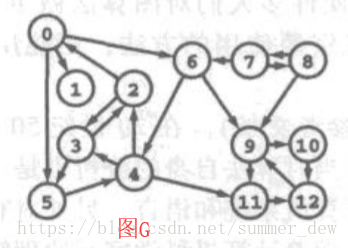
Kosaraju算法（有向图的强连通分量） - 图1
【步骤】

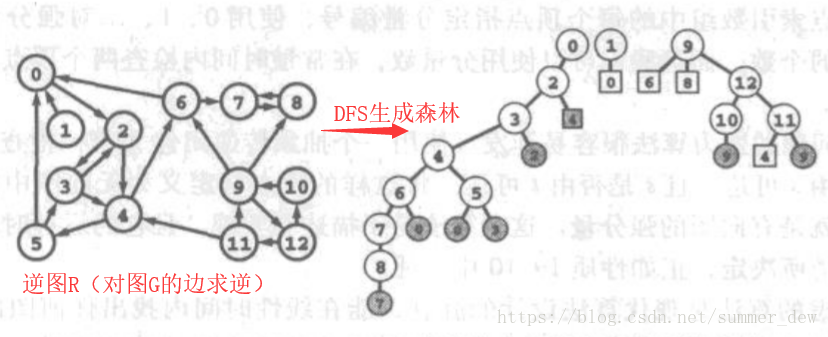
  1. 求图G的逆图R
  2. 对逆图R进行DFS，得到DFS生成森林
    Kosaraju算法（有向图的强连通分量） - 图2
  3. 求得生成森林的后序序列
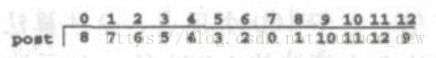
    Kosaraju算法（有向图的强连通分量） - 图3
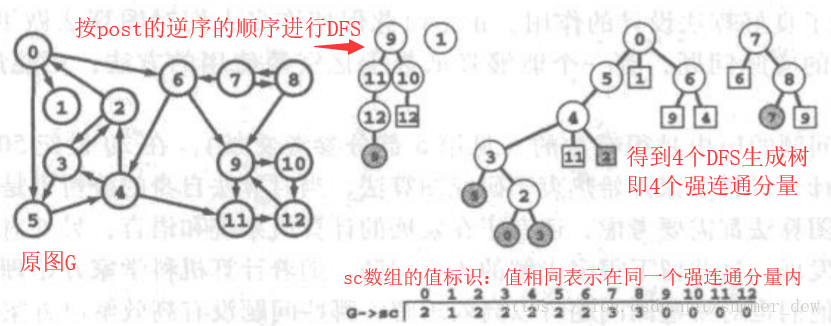
  4. 以逆图R的DFS后序数组（第三步的结果）后面往前的顺序，对原图G进行DFS，DFS得到的好几个生成树即是强连通分量
    Kosaraju算法（有向图的强连通分量） - 图4

伪代码

  1. #define maxV 100 //最大的顶点数
  2. int cnt0, cnt1;
  3. // 对图进行DFS，将DFS生成森林的后序序列放在post中
  4. int post[maxV]; //存放DFS生成森林的后序序列
  5. void SCdfsR(Graph *G, int w) { //对G从顶点w进行DFS
  6.     link t; //邻边
  7.     G->sc[w] = cnt1; //DFS访问标记
  8.     for (t=G->adj[w]; t!=NULL; t=t->next) //G的邻边
  9.         if (G->sc[t->v]==-1) SCdfsR(G, t->v); //G的邻接点还没有进行DFS
  10.     post[cnt0++]=w; //记录后序序列
  11. }
  12. // Kosaraju算法：求图G的强连通分量，记录在sc数组中
  13. int GraphSC(Graph *G) {
  14.     int v;
  15.     Graph R; //逆图G
  16.     int postR[maxV]; //逆图RDFS生成森林的后序序列
  18.     GraphReverse(*G, &R); //对G求逆图，存到R中
  19.     for (v=0; v<G->vernum; v++) R.sc[v]=-1; //逆图sc数组初始化
  21.     //对逆图R进行DFS
  22.     cnt0=0; cnt1=0;
  23.     for (v=0; v<G->vernum; v++)
  24.         if (R.sc[v]==-1) SCdfsR(&R, v);
  25.     //对图G进行DFS
  26.     cnt0=0; cnt1=0;
  27.     for (v=0; v<G->vernum; v++) G->sc[v]=-1; //sc数组初始化
  28.     for (v=0; v<G->vernum; v++) postR[v]=post[v]; //递归过程中post会被重新赋值-->将逆图R的后序序列拷贝到postR
  29.     //按照 逆图R的DFS生成树的后序序列 的逆序 顺序，来对图G进行DFS
  30.     for (v=G->vernum-1; v>=0; v--) {
  31.         if (G->sc[ postR[v] ]==-1) {
  32.             SCdfsR(G, postR[v]);
  33.             //第一次DFS退出
  34.             cnt1++; //进入下一个强连通分量
  35.         }
  36.     }
  37.     //销毁中间变量-逆图R
  38.     GraphDestory(&R);
  39.     return cnt1;
  40. }
  41. // 判断结点s,t是否为强连通
  42. int GraphStrongGraph(Graph G, int s, int t) {
  43.     return G.sc[s]==G.sc[t];
  44. }