AOV网
【AOV网】Activity On Vertex Network
- 用【顶点】表示活动
- 用【边】表示活动的先后顺序
- 没有回路
- 有向图
| 特点 | 说明 |
| —- | —- |
| 常用AOV网来表示一个工程的施工图或程序的数据流图 | AOV网描述了一种有实际意义的点,这种有实际意义的点自然有先后顺序 |
| AOV网不能有回路 | 【有回路的例子】 打地基->做房子结构->砌墙->装修->打地基
【解释】 “做房子结构“的前提是“打地基”,“砌墙”的前提是“做房子结构”,“装修”的前提是“砌墙”,“打地基”的前提是“装修”
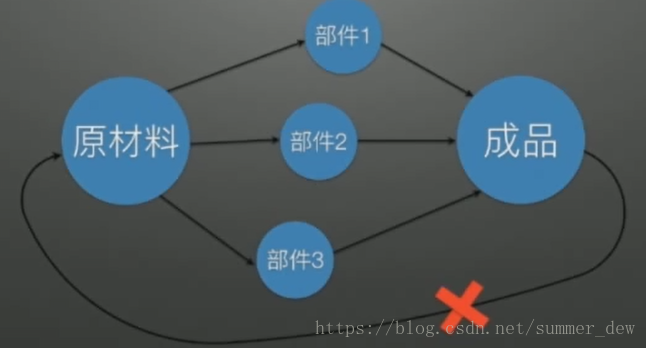
【说明】 到底是哪一个先开始,有回路就没法做了 | | AOV图可以可以导出很多种执行序列 | 【生产次序1】原材料->部件1->部件2->部件3->成品
【生产次序2】原材料->部件3->部件2->部件1->成品
【生产次序3】原材料->部件1->部件2->成品->部件3(×,部件3没有生产,成品不能先生产) |
拓扑排序
上面提到,AOV网可以导出很多种执行序列。那如何导出正确的执行序列呢?进行拓扑排序,拓扑排序的结果为拓扑排序序列,其即为正确的执行序列
【拓扑排序】按照有向图给出的次序关系,将图中顶点排成一个线性序列
【作用】
- 导出AOV网的执行序列(拓扑有序序列):一个有向图对应多个拓扑有序序列
- 检查有向图有没有环:拓扑排序结束后,如果图中还有顶点->有向图存在环
拓扑排序结果
情况1:新图中没有顶点
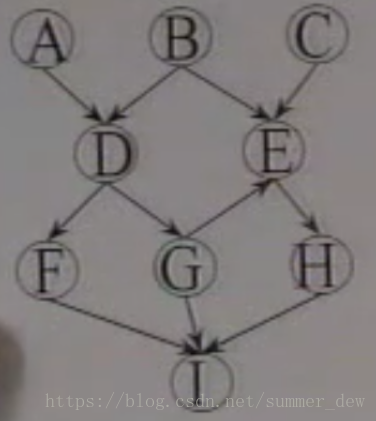
| 步骤数 | 入度为0的有 | 选择顶点 并删除顶点与弧 |
输出 |
|---|---|---|---|
| 1 | A,B,C | A | “A” |
| 2 | B,C | B | “AB” |
| 3 | D,C | D | “ABD” |
| 4 | F,G,C | F | “ABDF” |
| 5 | G,C | G | “ABDFG” |
| 6 | C | C | “ABDFGC” |
| 7 | E | E | “ABDFGCE” |
| 8 | H | H | “ABDFGCEH” |
| 9 | I | I | “ABDFGCEHI” |
删除至此,新图为空,没有结点了,说明没有回路,”ABDFGCEHI”即为【拓扑有序序列】
情况2:该有向图不是AOV网
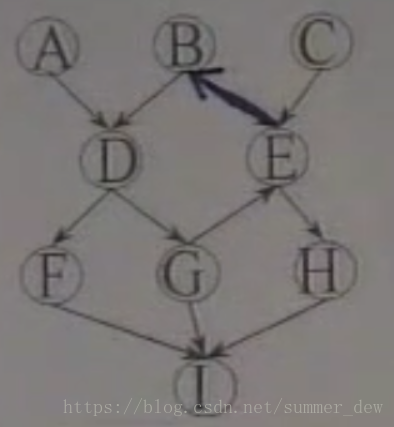
| 步骤数 | 入度为0的有 | 选择顶点 并删除顶点与弧 |
输出 |
|---|---|---|---|
| 1 | A,C | A | “A” |
| 2 | C | C | “AC” |
找不到入度为0的顶点=>退出=>图还没有空图=>有回路
拓扑排序代码-C语言
【数据结构】邻接表为例
需要将邻接表的数据结构加上一个count,表示入度
typedef struct VNode{char data;int count; //入度ArcNode *firstarc; //第一条边}VNode, AdjList[MAX_VERTEX_NUM];
【代码】
//计算每个顶点的入度
void CntGraphIndegree(ALGraph *pG) {
ArcNode *p;
int i;
for (i=0; i<pG->vernum; i++) {
for (p=pG->vers[i].firstarc; p; p=p->next) {
pG->vers[p->adjV].count++;
}
}
}
// 拓扑排序,并打印拓扑序列
int TopSort(ALGraph *pG) {
int i,j;
int n=0;
int stack[maxSize],top=-1; //保存当前所有入度为0的顶点
ArcNode *p;
CntGraphIndegree(pG); //计算入度
//将入度为0的顶点压入栈中
for (i=0; i<pG->vernum; i++) {
if (pG->vers[i].count==0)
stack[++top]=i;
}
while (top!=-1) {
i = stack[top--]; //顶点出栈,等效于在图中删掉
++n;
printf("%c ", pG->vers[i].data);
p=pG->vers[i].firstarc;
while (p!=NULL) {
j = p->adjV;
--(pG->vers[j].count);
if (pG->vers[j].count==0)
stack[++top]=j;
p=p->next;
}
}
if (n==pG->vernum) //拓扑排序后没有剩余顶点
return 1;
else //拓扑排序后还有剩余顶点
return 0;
}
【时间复杂度】O(n+e)
- 算法主体部分为一个单层循环和一个双层循环
- 单层循环:执行次数为n
- 双重循环:根据循环条件分析循环执行次数比较难
- 看进栈操作,因在无环情况下,每个结点恰好进栈一次 -> 进栈操作执行次数为n
- 分析入度减1的操作,在无环情况下,当排序结束时,每个边恰好被逻辑删除一次 ->入度减1操作执行次数为e
- 本算法中基本操作执行次数为n+n+e
- 因此时间复杂度为O(n+e)
逆拓扑排序
- 从有向图中选择一个出度为0的顶点输出
- 删除1中的顶点,并且删除指向该顶点的全部边
- 重复上述两步,直到剩余的图中不存在出度为0的顶点为止
方法一:拓扑排序修改
将拓扑排序的算法进行修改,将入度改成出度即可
方法二:深度优先遍历的方法
【原理】由于图中无环,当由图中某顶点出发进行DFS,最先退出算法的顶点即为出度为0的顶点,它是拓扑有序序列中的最后一个顶点
- 最先退出算法的顶点即是出度为0的顶点(先退出来的顶点没有邻边):退出算法指所遍历的顶点退出当前系统栈
- 按照DFS算法先后次序并不是指最终遍历结果序列,而是顶点退出系统栈的顺序
【例子】图{A->B,A->C,B->D,C->D}的DFS过程
| 操作 | 栈中元素 | 出栈元素 |
|---|---|---|
| A入栈 | A | |
| B入栈 | AB | |
| D入栈 | ABD | |
| D出栈 | AB | D |
| B出栈 | A | DB |
| C入栈 | AC | DB |
| C出栈 | A | DBC |
| A出栈 | DBCA |
- 因此,各个元素出栈先后序列为DBCA,为拓扑序列ACBD的逆拓扑序列
【实现】结点没有边的时候输出 —> 输出的是从尾到头的序列 —> 逆拓扑序列
void DFS(int v, ALGraph *pG) {
visit[v] = 1;
ArcNode *q = pG->vers[v].firstarc;
while (q!=NULL) {
if (visit[q->adjV]==0)
DFS(q->adjV, pG);
q=q->next;
}
Visit(v); //v的邻边都被访问过了,再输出
//第一个输出的,就是v没有邻边-->即末端的结点
}
附:拓扑排序完整代码-C语言
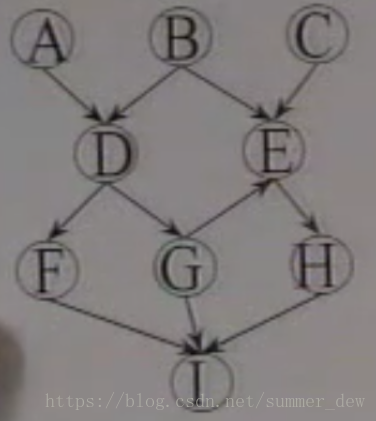
| 测试数据 | 结果 |
|---|---|
 |
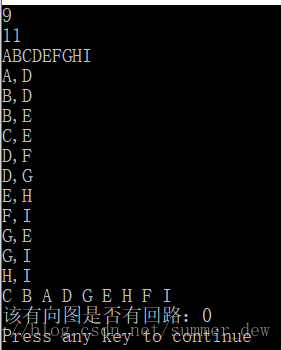 |
【完整代码】
#include<stdio.h>
#include<stdlib.h>
#define maxSize 50
#define MAX_VERTEX_NUM 20
#ifndef BASE
#define BASE
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW -2
typedef int Status;
typedef int bool;
#endif
typedef struct ArcNode{
int adjV;
struct ArcNode *next;
}ArcNode;
typedef struct VNode{
char data;
int count; //入度
ArcNode *firstarc; //第一条边
}VNode, AdjList[MAX_VERTEX_NUM];
typedef struct{
int vernum,arcnum;
AdjList vers;
}ALGraph;
/*------------------------
|创建有向图的邻接表 |
------------------------*/
Status InitGraph_AL(ALGraph *pG) { //初始化
int i;
pG->arcnum = 0;
pG->vernum = 0;
for (i=0; i<MAX_VERTEX_NUM; ++i)
pG->vers[i].firstarc = NULL; //VC++6.0中指针初始化为0xcccccccc
return OK;
}
int LocateVex_AL(ALGraph G, char e) { //定位值为e的元素下标
int i;
for (i=0; i<G.vernum; ++i) {
if (G.vers[i].data == e) {
return i;
}
}
return -1;
}
Status CreateDG_AL(ALGraph *pG) { //创建有向图的邻接表--不带权
//输入规则:顶点数目->弧的数目->各顶点的信息->各条弧的信息
int i,a,b;
char tmp[MAX_VERTEX_NUM];
char h,t;
ArcNode *p, *q;
InitGraph_AL(pG); //VC++6.0中指针初始化为0xcccccccc,如果不将指针初始化为NULL,会出错
//顶点数目
scanf("%d", &i); if (i<0) return ERROR;
pG->vernum = i;
//弧的数目
scanf("%d", &i); if (i<0) return ERROR;
pG->arcnum = i;
//各顶点信息
scanf("%s", tmp);
for (i=0; i<pG->vernum; ++i) {
pG->vers[i].data=tmp[i];
pG->vers[i].count=0;
}
//弧的信息
for (i=0; i<pG->arcnum; ++i) {
scanf("%s", tmp);
h = tmp[0]; t = tmp[2];
a = LocateVex_AL(*pG, h);
b = LocateVex_AL(*pG, t);
if (a<0 || b<0) return ERROR;
p = (ArcNode *)malloc(sizeof(ArcNode)); if (!p) exit(OVERFLOW);
p->adjV=b;p->next=NULL;
if (pG->vers[a].firstarc) { //已经有边了
for (q = pG->vers[a].firstarc; q->next; q=q->next) ; //找到最后一条
q->next = p;
} else { //第一条边
pG->vers[a].firstarc = p;
}
}
return OK;
}
//计算每个顶点的入度
void CntGraphIndegree(ALGraph *pG) {
ArcNode *p;
int i;
for (i=0; i<pG->vernum; i++) {
for (p=pG->vers[i].firstarc; p; p=p->next) {
pG->vers[p->adjV].count++;
}
}
}
// 拓扑排序,并打印拓扑序列
int TopSort(ALGraph *pG) {
int i,j;
int n=0;
int stack[maxSize],top=-1; //保存当前所有入度为0的顶点
ArcNode *p;
CntGraphIndegree(pG); //计算入度
//将入度为0的顶点压入栈中
for (i=0; i<pG->vernum; i++) {
if (pG->vers[i].count==0)
stack[++top]=i;
}
while (top!=-1) {
i = stack[top--]; //顶点出栈,等效于在图中删掉
++n;
printf("%c ", pG->vers[i].data);
p=pG->vers[i].firstarc;
while (p!=NULL) {
j = p->adjV;
--(pG->vers[j].count);
if (pG->vers[j].count==0)
stack[++top]=j;
p=p->next;
}
}
if (n==pG->vernum) //拓扑排序后没有剩余顶点
return 1;
else //拓扑排序后还有剩余顶点
return 0;
}
int main() {
/*
测试数据:没有回路
9
11
ABCDEFGHI
A,D
B,D
B,E
C,E
D,F
D,G
E,H
F,I
G,E
G,I
H,I
测试数据二:有回路
9
11
ABCDEFGHI
A,D
B,D
C,E
D,F
D,G
E,B
E,H
F,I
G,E
G,I
H,I
*/
ALGraph G;
int ret;
CreateDG_AL(&G);
ret = TopSort(&G);
printf("\n该有向图是否有回路:%d\n", !ret);
return 0;
}

