胜者树/败者树

【胜者树/败者树】

  1. 都是完全二叉树，是树形选择排序的一种变形。每个叶子结点相当于一个选手，每个中间结点相当于一个比赛，每一层相当于一轮比赛
  2. 不同：胜者树中间结点记录的是胜者的标号；而败者树的中间结点是记录败者的标号

【评价】

  1. 胜者树/败者树可以在log(n)的时间内找到最值
  2. 任何一个叶子结点的值改变后，利用中间结点的信息，还能够快速地找到最值

败者树

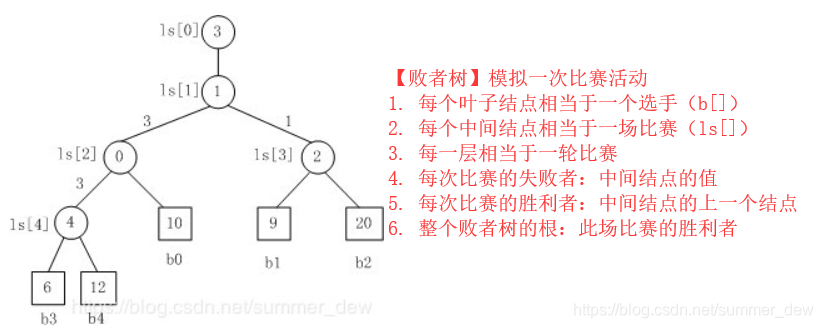
选择树（胜者树、败者树） - 图1
【数据结构】两个数组

  1. b[]：下标i为选手的号码，b[i]为选手的能力
  2. ls[]：存放败者的记录，ls[0]为正常的胜利者

【建树】两个子节点比较(b3、b4)，败者(b4)放入它们的父结点(ls[4])，而胜者(b3)送到它们的父结点的父结点再和别人PK。如此重复，即可以把最后的胜者推到败者树根结点的父结点中（如图ls[0]）

【调整】胜者（b[3]）从树中被摘除，然后有新的元素替换胜者的位置（b[3]）

  1. 新的元素（b[3]）和它的父结点（ls[4]）继续比较，PK后败者放入父结点中，胜者被送上去继续PK

【优点】在继续比较时，它不用和所有叶子的关键字比较，只需沿着相应的叶子结点到根结点的路径调整败者树，这样可以减少比较次数

【代码】

  1. #define LEN 5//败者树容量，多路归并数目
  2. #define MIN -1//所有数据的可能最小值
  4. int ls[LEN+1];//败者树,ls[0]存放胜者，其余存放败者
  5. int buf[LEN+1];//存放多路归并的头元素值,多出来的一位放MIN
  7. //当改变一个选手的值，需要调整以维持败者树的形态。败者树只需调整选手的父节点即可
  8. //1. 当子节点的值大于父节点，则子节点记录于父节点（小为胜利，记录败者），父节点继续与其父节点比赛
  9. //2. 若子节点小于父节点，则直接使用子节点进行下一轮比赛。
  10. void adjust(int s,int *buf){//s是需要调整的buf的下标
  11.     int t=(s+LEN)/2;//得到s的在败者树上面的父节点
  12.     while(t>0){//不断与父节点对比，直到败者树的根节点
  13.         if(buf[s]>buf[ls[t]]){//如果当前节点s（胜者）大于父节点
  14.             ls[t]^=s;//交换ls[t]和s
  15.             s^=ls[t];//s记录胜者
  16.             ls[t]^=s;//父节点记录败者
  17.         }
  18.         t/=2;//得到败者树的上一个父节点，继续与当前胜者s比较
  19.     }
  20.     ls[0]=s;//最终的胜者记录于ls[0]
  21. }
  23. // 在参赛者数组b[]的最后添加一位，存放一个参赛选手的绝对最小值（选手都是正数的话，如-1）
  24. // 所有中间节点都记录这个最小值的下标。然后依次调整（adjust()）各个选手即可
  25. void build(int *buf){
  26.     buf[LEN]=MIN;//最后一位放MIN
  27.     for(int i=0;i<LEN+1;++i)
  28.         ls[i]=LEN;//所有败者树初始化为MIN的下标
  29.     for(i=0;i<LEN;++i)
  30.         adjust(i,buf);//依次调整即可完成初始化
  31. }
  33. int main()
  34. {
  35.     //初始buf
  36.     int tmp[5]={18,21,16,11,19};
  37.     memcpy(buf,tmp,LEN*sizeof(int));
  38.     build(buf);
  39.     cout<<buf[ls[0]]<<endl;//输出11
  41.     //取出11后，buf[3]=17
  42.     int tmp1[5]={18,21,16,17,19};
  43.     memcpy(buf,tmp1,LEN*sizeof(int));
  44.     adjust(3,buf);
  45.     cout<<buf[ls[0]]<<endl;//输出16
  47.     return 0;
  48. }

【应用】

  1. 败者树：外部排序中的应用