@[toc]
| 概念 | 说明 |
|---|---|
| 哈希表or散列表 | 根据关键字的值来计算出关键字在表中的地址 |
| 将关键字映射到地址上;H(key)是key的Hash地址 | |
| H(key)出现冲突后,再key经过第i次冲突解决后的地址 |
哈希表(散列表)
- 哈希函数:选择一个好的哈希函数,产生的冲突会比较少
- 冲突处理:选择一种处理冲突的方法
哈希函数
【哈希函数】把key转换为address的一个函数
【选择原则】建表的关键字集合的情况(包括关键字的范围和形态),总的原则是使产生冲突的可能性降到尽可能地小
【关键字】
- 若关键字是非数字,则要先对关键字进行数字化处理,转换成数字类型
- 若关键字是数字,哈希函数则有以下类型
| 方法名 | 介绍 | 特点(适用于) | 公式或例子 | 说明 |
| —- | —- | —- | —- | —- |
| 直接定址法 | 取关键字或关键字的某个线性函数为Hash地址 | 地址集合的大小=关键字集合的大小 |
%3Dkey#card=math&code=H%28key%29%3Dkey&id=zaWQM)或
%20%3D%20a%C3%97key%2Bb#card=math&code=H%28key%29%20%3D%20a%C3%97key%2Bb&id=DSPIP) | 其中:a和b为常数 | | 数字分析法 | 分析的原则:尽量取冲突较少的位数段 | 1. 关键字位数比较多
2. 表中关键字都是已知的 | | 电话号码后4位的重复几率较少 |
| 平方取中法 | 取关键字平方后的中间几位作为Hash地址 | 1. 放到了数字,产生的冲突较少
| 电话号码后4位的重复几率较少 |
| 平方取中法 | 取关键字平方后的中间几位作为Hash地址 | 1. 放到了数字,产生的冲突较少
2. 关键字中的每一位都有某些数字重复出现频度很高的现象 | 关键字123,123²=15129,取512做为哈希地址 | 一个数平方后的中间几位数和数的每一位都相关,由此得到的Hash地址随机性更大 | | 除留余数法 | 取关键字被某个小于等于Hash表表长m的数p除后所的余数为Hash地址 | | | 一般p≤len的最大素数,p不含20以下的质因子,这样可以减少冲突 |
| 折叠法 | 将关键字分割成若干部分,然后取它们的叠加和为哈希地址 | 关键字的数字位数特别多 | 移位叠加
| 一般p≤len的最大素数,p不含20以下的质因子,这样可以减少冲突 |
| 折叠法 | 将关键字分割成若干部分,然后取它们的叠加和为哈希地址 | 关键字的数字位数特别多 | 移位叠加
间界叠加 | | | 随机数法 | | 用于对长度不等的关键字构造哈希函数 |H(key) = Random(key)| |
冲突解决方法
【冲突】不同的元素经过哈希函数映射到同一位置上,导致了位置重叠
【冲突处理方法】为产生冲突的地址寻找下一个哈希地址
【解决冲突后的地址】#card=math&code=H_i%28key%29&id=d2WHW) :是对key经过i次冲突解决后的地址
开放地址法
【开放地址法】位置上已经有人了,我就找别的位置
| 每次的增量di的取法 | 介绍 | 特点 | 公式 | 说明 |
|---|---|---|---|---|
| 线性探查法(线性探测再散列) | 一次往后走i | 可以探测到表中所有位置,但是容易产生【堆积】问题 | 【堆积问题】原来,A和B经过哈希函数,不会地址冲突,而后来B的位置被A占了,导致了堆积,致使B又要往后移 | |
| 平方探查法(平方探测再散列) | 走的距离d是平方变化的 | 不可探测到表中所有位置(至少可以探测到一半位置) 不易产生堆积问题 |
d:发生冲突的地址 新地址为  |
平方探测发是一种较好的处理冲突的方法,可以避免堆积问题 缺点:不能探查到Hash表上的所有单元,但至少能探查到一半的单元 |
| 随机探测再散列(伪随机序列法) | 每次探测的距离是一个随机数 |  di是一组伪随机数列 di是一组伪随机数列 |
||
| 双Hash函数法 | Hash地址为H( H(k) ) |
【增量di应具有“完备性”】产生的Hi均不相同,且所产生的s(m-1)个Hi值能覆盖哈希表中的所有地址
- 平方探测时的表长m必为形如4j+3的素数(如:7、11、19、23…等)
- 随机探测时的m和d没有公因子
链地址法
【链地址法】将冲突的元素用地址链起来
【举例:查找失败的次数】key=A。若H(A)=9,即A这个关键字的值映射的地址是9
那么要比较几次关键字才知道查找失败呢?
- 先与100比较
- 再与9比较
- 最后发现空指针NULL
【第一种说法】这里比较了2次
【第二种说法】但有些教材与学校把和空指针比较也算一次,那就是3次了
但一般是说法一,毕竟指针的判别,不是【关键字比较】
装填因子
【装填因子】表中关键字填满的程度
【注意】
性能分析
了解各种冲突解决方法所对应的平均查找长度随装填因子a的变化趋势即可
| 解决冲突的方法 | 成功的ASL | 不成功的ASL |
|---|---|---|
| 线性探查法 | ||
| 平方探查法 | ||
| 链地址法 | ||
| 说明 | a为装填因子 |
| ASL | 求法 |
|---|---|
| 查找成功的ASL | 找到表中元素的平均比较次数 |
| 查找不成功的ASL | 所有可能散列到的地址上插入一个新元素时,为找到空位置而进行探查的平均次数 |
【注】无特殊说明
- 在顺序表的存储结构下,如果空位置作为结束标记,则与空位置的比较次数也要计算在内
- 在链表的存储结构下,与空指针的比较次数不计算在内
求散列表的一般步骤
- 计算表长:
(注意要向上取整)
- 计算p:取不大于L的最大素数(重点)
- 根据哈希函数、冲突机制计算哈希表
- 成功ASL:表中关键字查找次数之和/关键字总数
- 失败ASL:表中所有能够映射到的位置查找次数之和/位置总数
例题
| 例题 | 计算 |
|---|---|
| 关键字{7, 8, 30, 11, 18, 9, 14}; 存储空间:从0开始的一维数组 H(key)= ( key × 3 ) Mod 7; 线性探测再散射法; 装填因子0.7 |
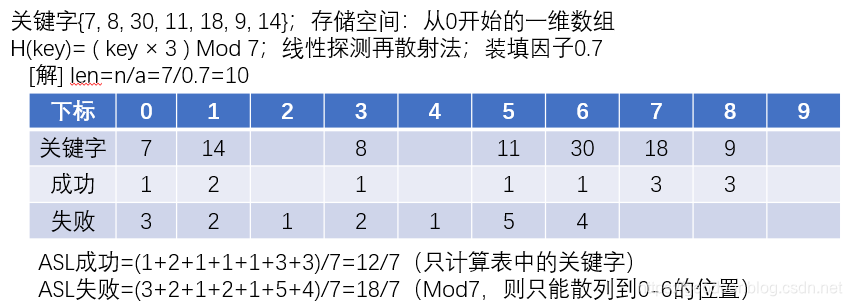 |
| 关键字{7, 4, 1, 14, 100, 30, 5, 9, 20, 134} H(key) = key Mod 13; 线性探测法; 表长为15 |
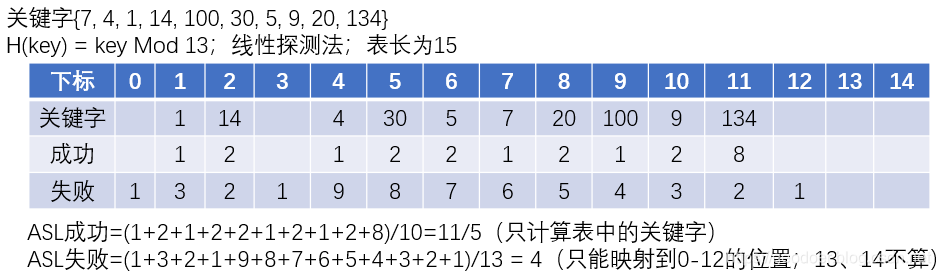 |
| 关键字{1, 9, 12, 11, 25, 35, 17, 29} 装填因子a=0.5; 除留余数构造Hash函数; 链地址法处理冲突 |
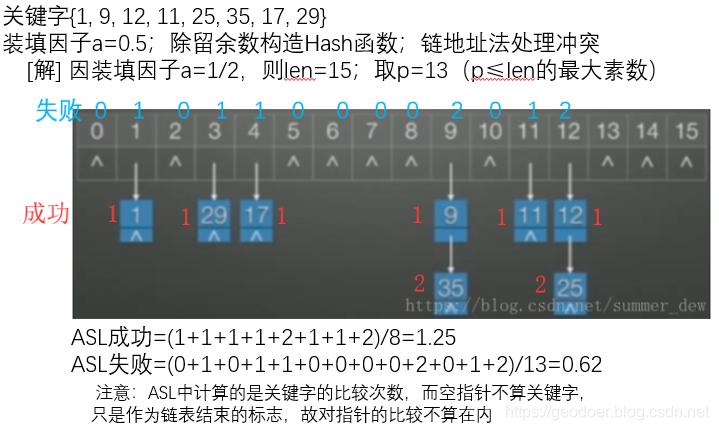 |
| 假设有k个关键字互为同义词,若用线性探查法把这k个关键字存入散列表,至少要进行()探测 | 探测:查看了多少次里面有没有人 |

