图
基础概念
【网】边上带有权的图成为带权图,也称网
| 概念组 | 无向图 | 有向图 |
|---|---|---|
| 【完全图】任意两点都有边 | 【无向完全图】具有 |
【有向完全图】具有 |
| 【连通】两点有路径 | 【连通图】任意两点有路 【连通分量】即极大连通子图 |
【强连通图】任意两点AB,A到B、B到A都有路 【强连通分量】即极大强连通子图 |
| 【极小】 1. 当前子图中两两已连通 2. 目前边最少,再添加一条边,就会构成一个环(讨论生成树) |
【极小连通子图】连通图的生成树 1. 同一个连通图的生成树不唯一 2. 极小连通子图只存在于连通图中 |
|
| 【极大】不能再大(讨论连通分量的) | 【极大连通子图】 - 【连通图】只有一个极大连通子图,就是它本身 -【非连通图】有多个极大连通子图 |
【极大强连通子图】 - 【强连通图】只有一个极大强连通子图,它本身 - 【非强连通图】有多个极大强连通子图 |
存储结构
| 存储结构 | 图解 | 定义 |
|---|---|---|
| 邻接矩阵 |  |
|
| 邻接表 |  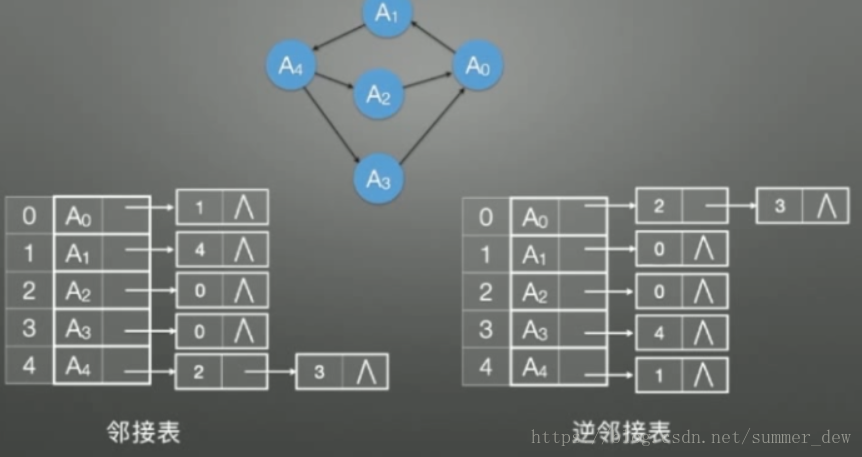 |
 |
| 有向图的十字链表 | 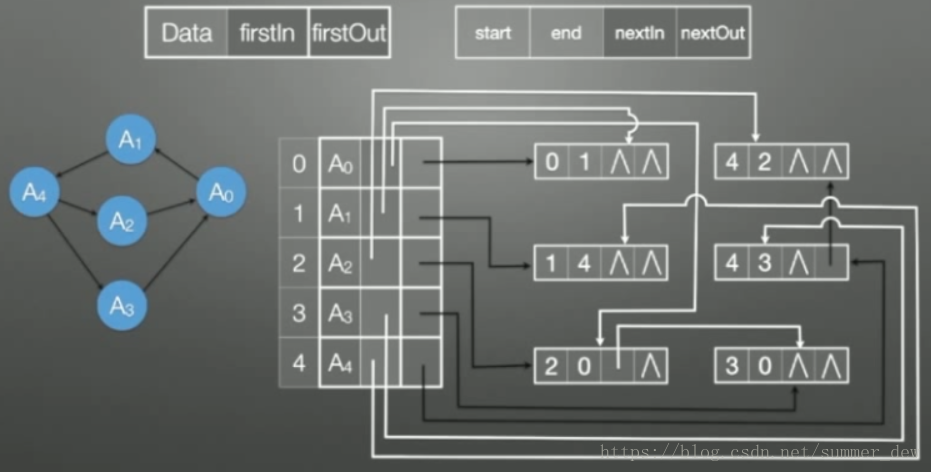 |
 |
| 无向图的邻接多重表 | 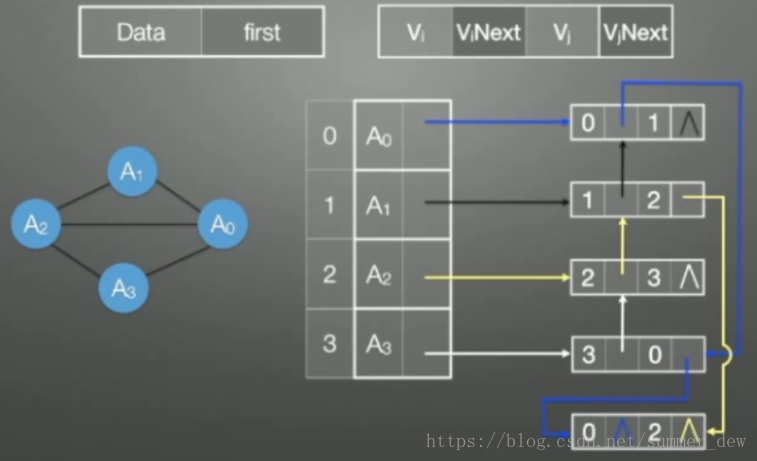 |
 |
遍历(邻接表示例)
| 遍历 | 递归 | 非递归 |
|---|---|---|
| DFS O(n+e) |
 |
 |
| BFS O(n+e) |
 |
【BFS时间复杂度】算法主体为一个双重循环,基本操作有两个:顶点进队;边访问。最坏情况为遍历图中的所有顶点后才找到通路,此时所有顶点都进队一次,所有边都被访问一次,因此总次数为n+e,即O(n+e)
(无向连通图的)最小代价生成树
【无向连通图的生成树】删除边—>①只剩下n-1条边;②任意两点还是连通的
【最小生成树】一个无向连通图的生成树有很多,边权重之和最小的那一棵
【什么时候无向连通图的最小生成树是唯一的?】①所有边的权重不同;②边相同,但只有n-1条边
【最小生成森林】针对非连通图而言,删除边,将图变成一对多的关系
| Prim普利姆 | Kruskal克鲁斯卡尔 | |
|---|---|---|
| 思想 | ①以顶点为操作对象,每次选择一个顶点并入子图; ②顶点的选择依据:子图到其他顶点的最短路径 |
①以边为操作的主要单位:每次并入一条边; ②选择边的依据:当前最小边,且不构成回路 |
| 数据结构 | ①子图vest[i]:结点i是否已并入生成树; ②lowcost[i]:结点i到子树的最短边权重 |
①Road:存储图的所有边 ②用并查集 检查是否构成回边 |
| 适合 | 稠密图(时间复杂度与顶点有关系,与边数没有关系) | 稀疏图(时间复杂度由边数决定) |
| 时间复杂度 | ||
| 示例 | 最小生成树-邻接表Prim | |
| 代码 |  |
 |
最短路径
| 算法 | 用途 | 思想 | 时间复杂度 | 应用 |
|---|---|---|---|---|
| BFS算法改造 | 两点间最短路径 | |||
| 迪杰斯特拉算法Dijkstra | 某一个顶点到其余各顶点的最短路径 | ①以顶点为操作对象,每次选择一个顶点并入子图; ②顶点选择依据:起点到其他顶点的最短路径 |
博客 | |
| 弗洛伊德算法Floyd | 任意两点的最短路径 | ①将每个顶点都作为中转站; ②每两个顶点经过中转站是否会更近 |
- 原理 - 医院选址问题 |
迪杰斯特拉算法
| 举例 | 手算答题模板 |
|---|---|
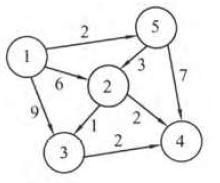 |
用dist[]存放最短路径长度,path[]存放最短路径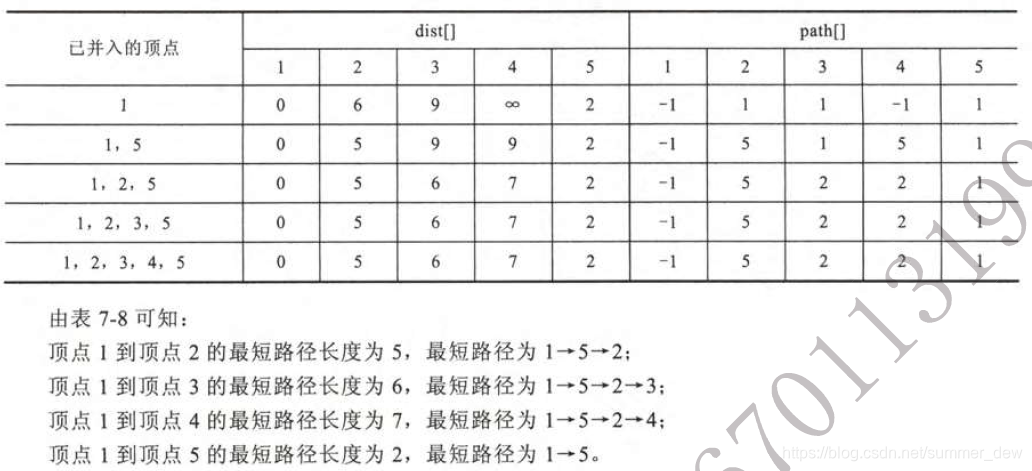 |
void printPath(int path[], int a) {int stack[maxSize], top = -1;// 以由叶子结点到根结点的顺序将其入栈while (path[a]!=-1) {stack[++top] = a;a = path[a];}stack[++top] = a;while ( top!=-1 ) {//出栈并打印出栈元素,实现了顶点逆序打印printf("%d ", stack[top--]);}printf("\n");}#define INF 10e6void Dijkstra(MGraph G, int v0, int dist[], int path[]) {//dist[i]:v0到i的最短路径的值//path[i]:v0到i最短路径中,i的前一个顶点int set[maxSize]; // 已考虑的顶点int min, i, j, u;// 初始化:从v到其他各点for (i=0; i<G.vernum; ++i) {dist[i] = G.arcs[v0][i]; //v0->iset[i] = 0;if (G.arc[v0][i]<INF) path[i] = v;else path[i] = -1;}set[v0] = 1; path[v0] = -1;for (i=1; i<=G.n; ++i) { // 还需要考虑n-1个顶点// 选出一条权值最短的边min = INF;for (j=0; j<G.vernum; ++j) {if ( set[j]==0 && dist[j]<min ) {u = j;min = dist[j];}}set[u] = 1; //并入集合// 更新dist:经过顶点u会不会更近呢?for (j=0; j<G.vernum; ++j) {if (set[j]==0 && dist[u]+G.edges[u][j]<dist[j]) {dist[j] = dist[u] + G.edges[u][j]; //v0->u->jpath[j] = u;}}}}
弗洛伊德算法
| 举例 | 手算答题模板 |
|---|---|
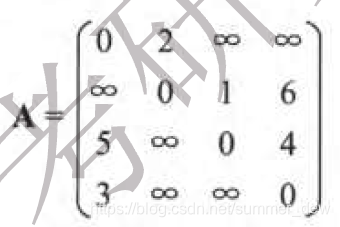 |
 |
void PrintPath(MGraph G, int u, int v, int path[][max]) {int midNode;if ( path[u][v]==-1 ) {print("<%C,%c>", G.vers[u], G.vers[v]); //直接输出} else {mindNode = path[u][v];PrintPath(u, mid, path); //mid前半段路径PrintPath(mid, v, path); //mid后半段路径}}void Floyd(MGraph G, int A[][maxSize], int Path[][maxSize]) {int i,j,k;// 初始化for (i=0; i<G.n; i++) {for (j=0; j<G.n; j++) {A[i][j] = G.edges[i][j];Path[i][j] = -1;}}for (k=0; k<G.n; ++k) { //中间经过k点有没有更近呢?for (i=0; i<G.n; ++i) {for (j=0; j<G.n; ++j) {// i->j 对比 i->k->jif (A[i][j]>A[i][k] + A[k][j]) {A[i][j] = A[i][k] + A[k][j];Path[i][j] = k;}}}}}
AOV、AOE网
| AOV网 | AOE网 | |
|---|---|---|
| 例子 |  |
 |
| 介绍 | 【有向无环图】活动在顶点上网(Activity On Vertex network,AOV) | 【有向无环图】活动在边上的网(Vctivity On edge network) |
| 边 | 边无权值,代表活动之间先后次序 | 边表示活动,且有权值,代表活动持续时间 |
| 顶点 | 顶点表示活动 | 顶点代表事件,事件是图中新活动开始、旧活动结束的标志 |
AOV网
| 拓扑排序(拓扑有序序列) | 逆拓扑排序(逆拓扑有序序列) |
|---|---|
| ①拓扑排序算法改进;②DFS算法:ALGraph没有邻边的时候输出 | |
 |
 |
AOE网
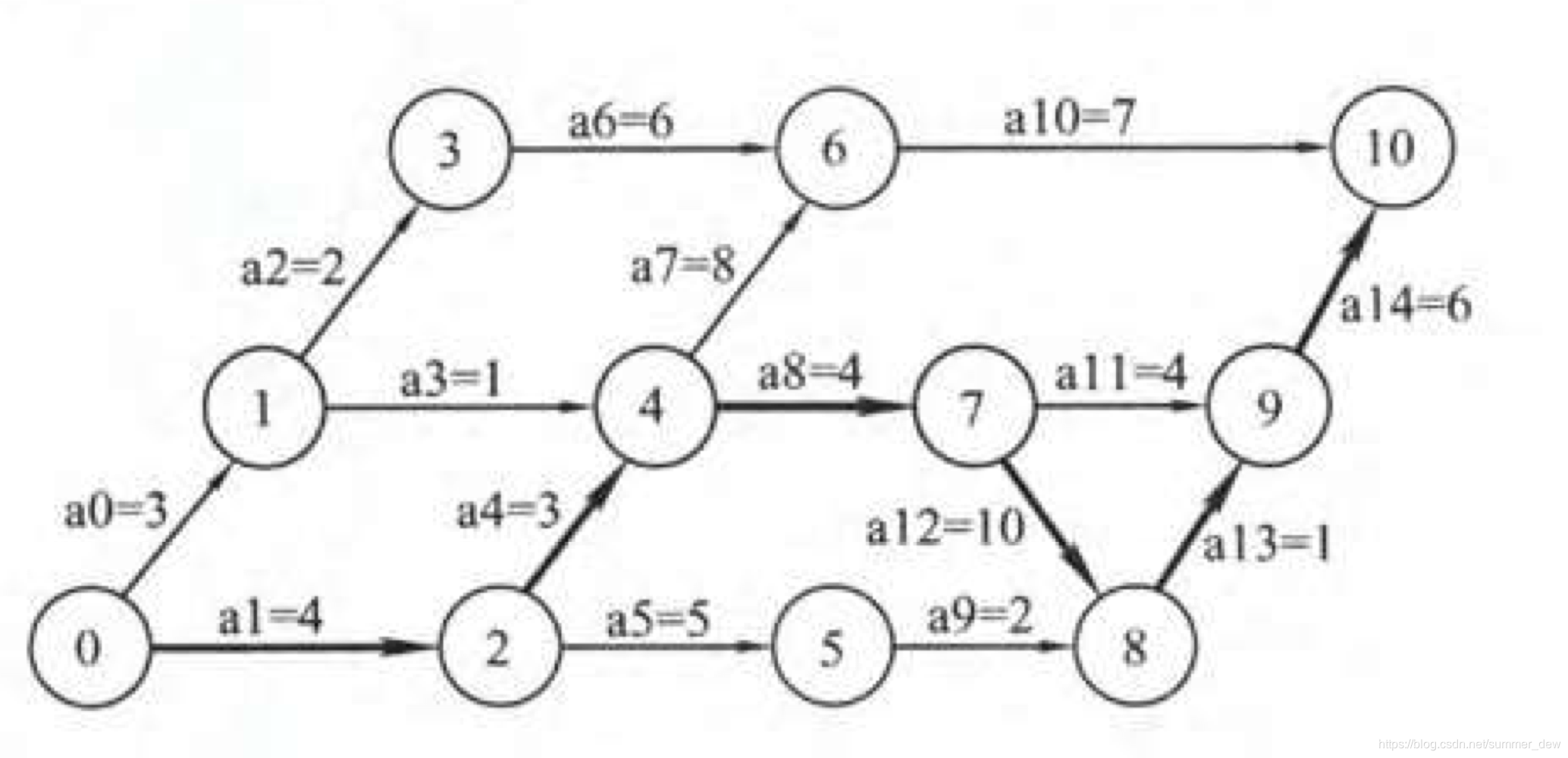
| 概念1 | 说明 | 概念2 | 说明 |
|---|---|---|---|
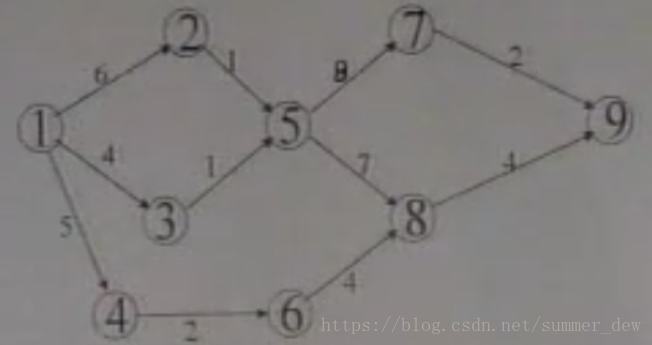
| ve(vertex earliest)事件最早发生时间 | 若事件4要发生,事件4的上游0、1、2都要先发 【即】事件4的最早发生时间ve(4)=0到4的最长路径=7 |
vl(vertex latest)事件的最迟发生时间 | 1. 根据关键路径得到工程结束的最短时间为28天 2. 事件7距离完成需要17天(7-10有两条路,取时间大的:①7->9->10的时间要10天,②7->8->9->10要17天) 3. 那么,事件7最迟要在第11天开始!不然28天就完不成了! 【即】vl(7)=28-17=11 |
| ee(edges earliest)活动的最早发生时间 | 【解释】a7、a8的最早发生时间,即是事件4的最早发生时间,如ee(a7)=ee(a8)=ve(4)=7 【算法】ee(z)=ve(k)顶点k是边z的头顶点 【例】边a3的头顶点是1:ee(a3)=ve(1)=3 |
el(edges latest)活动的最迟发生时间 | 【解释】a8的最迟发生时间=vl(7)-a8的权重=vl(7)-4=7 【算法】el(z)=vl(k)-z顶点k是边z的尾顶点 【例】边a14的尾顶点是10:el(a14)=vl(10)-a14=28-6=22 |
| 关键活动 | ee=el的活动 | 关键路径 | 关键活动构成的路径(可能有多个);图中最长的路径;关键路径之和为整个工程的最短时间 |
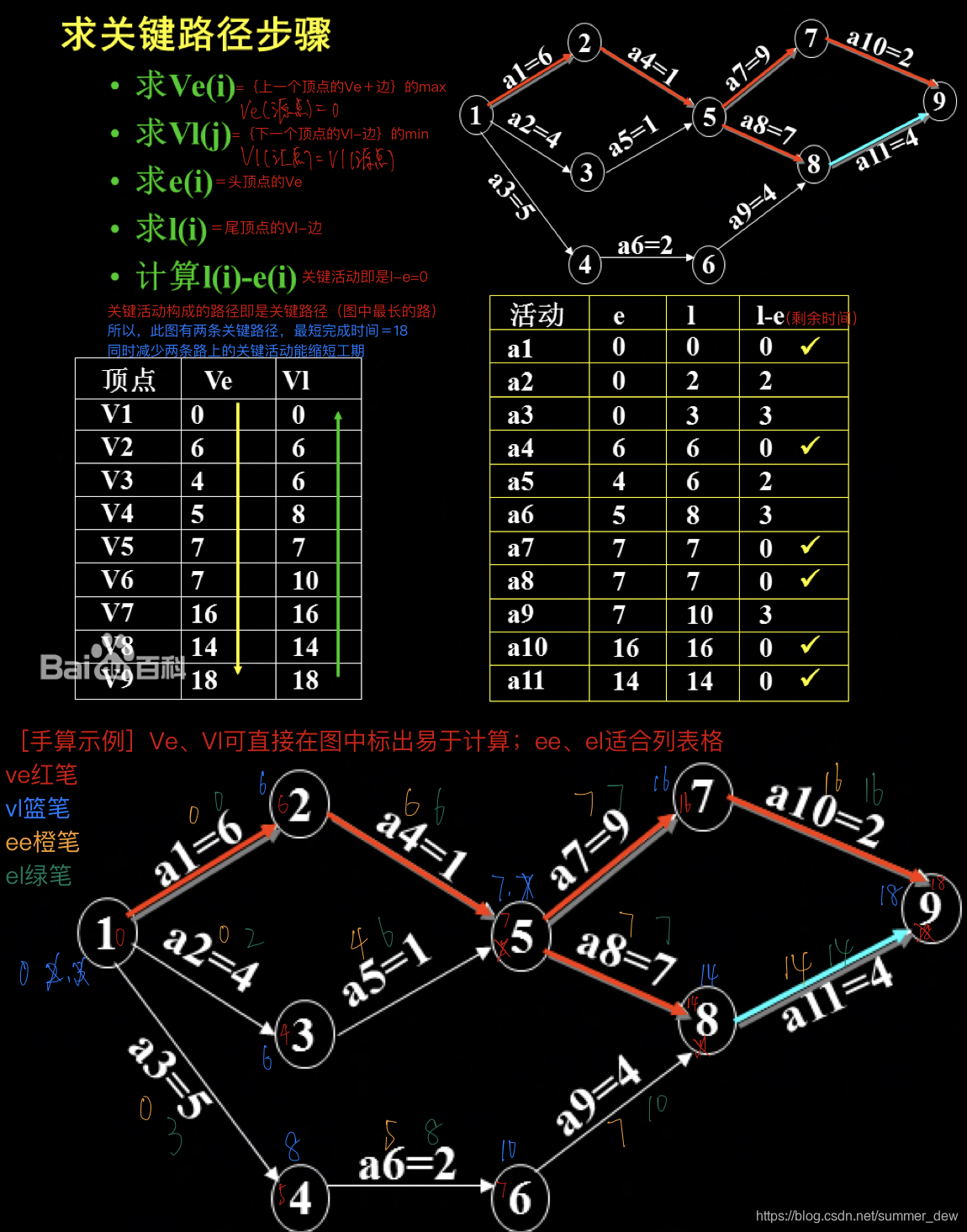
扩展
| 超纲的问题 | 应用 |
|---|---|
| 无向图的连通分量和生成树 | 无向图的连通分量和生成树-DFS |
| 有向图的强连通分量 | - 介绍 - 手算方法 |
| 关节点 与 重(双)连通图 | 详情 |

