思想

为使生成树上边的权值之和达到最小，则应使生成树中每一条边的权值尽可能地小。

【理解】

  1. 每一轮选一个最小的边，将边的顶点并入生成树中，直到全部顶点都在生成树中
  2. 显然，第一步是不完整的，如果选的边构成了环怎么办？所以，并入最小边的时候，还需要考虑是否形成环
    • 若该边并入后形成环：那就不并入了，继续找下一个最小边
    • 若该边不会形成环：并入，继续

【如何判断是否会构成环？】https://blog.csdn.net/summer_dew/article/details/83036947

性能

O(eloge)，适合稀疏图（边少的图）
另一个，普利姆Prim O(n^2)：适合稠密图（边多的图）
博客：https://blog.csdn.net/summer_dew/article/details/81660483

举例

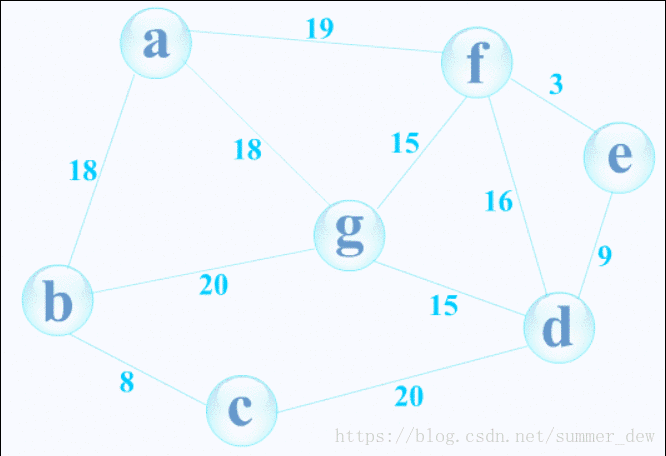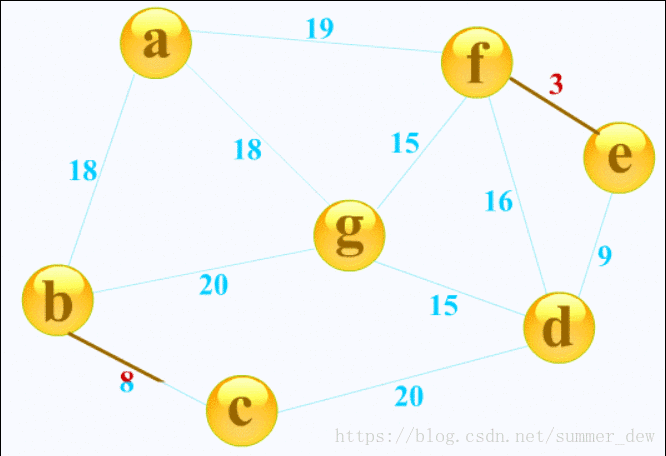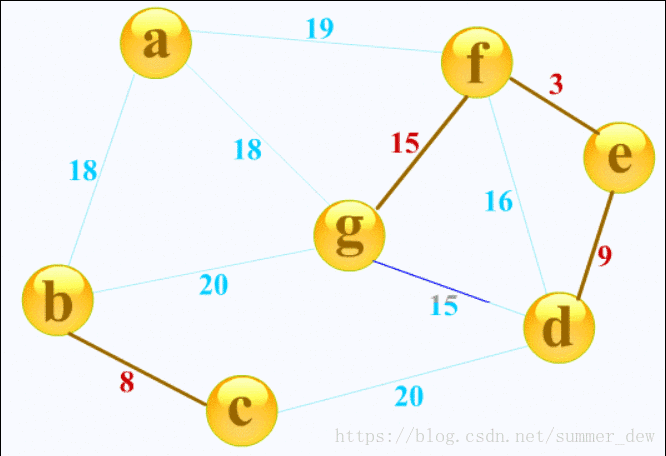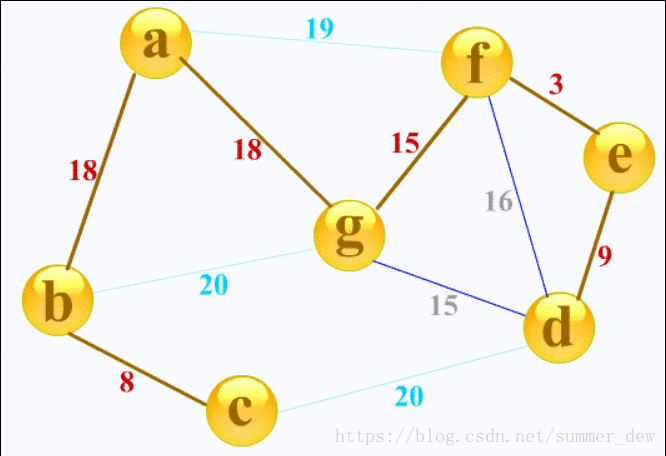
初始：将所有的顶点纳入考虑（变黄色），所有的边纳入考虑（蓝色）

  1. 选取所有边中（蓝边）最小的边f-e(权重为3)，纳入生成树的边（变棕色）
  2. 将边的两个顶点纳入生成树的顶点【e,f】
  3. 若生成树顶点中【e,f】有互联的线，变深蓝色，不考虑<=因为不能产生回边
  4. 当有n-1条边完成，退出

Kruskal（最小生成树） - 图1

实现案例

例子来源：天勤论坛数据结构课程http://www.csbiji.com

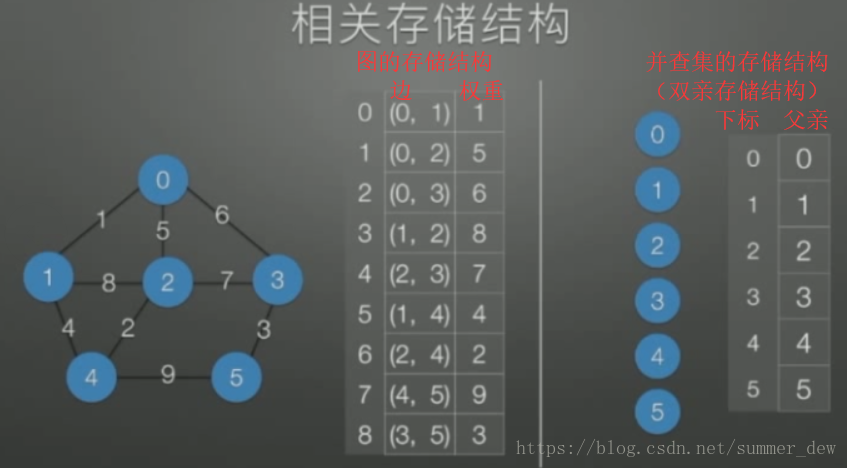
【相关的存储结构】

  1. 左边的数组：存储着图的所有边与边的权重，用结点的下标代表顶点的信息（简化版的树，树的顶点信息为数字）
  2. 右边的数组：并查集，使树的双亲存储结构
    Kruskal（最小生成树） - 图2
  1. //边的结构
  2. typedef struct{
  3.     int a,b; 
  4.     int w; //权重
  5. }Road;
  6. Road road[maxSize];
  7. //并查集的结构
  8. int v[maxSize];
  9. //得到p的根结点
  10. int getRoot(int p) {
  11.     while (p!=v[p]) //当p==v[p]时，即找到了根结点
  12.         p = v[p];
  13.     return p; //只有根结点的父亲是它自己
  14. }
  15. // 克鲁斯卡尔算法
  16. // road[]：边集
  17. // n：顶点数
  18. // e：边的个数
  19. int Kruskal(Road road[], int n, int e) {
  20.     int sum=0;
  21.     int a,b;
  22.     int i;
  23.     for (i=0; i<n; ++i) v[i]=i; //构造并查集的初始状态，各个节点为单独的树（即它的父亲都为它们自己）
  24.     sort(road, e); //将边数组，从小到大排序
  25.     for (i=0; i<e; ++i) { //遍历边数组，边数组已经被排序过了，从小到大-->从头到尾扫描即可
  26.         a = getRoot(road[i].a);
  27.         b = getRoot(road[i].b);
  28.         if (a!=b) { //不会构成环
  29.             v[a] = b; //更新并查集
  30.             sum += road[i].w; //将边加入生成树
  31.         }
  32.     }
  33. }