【问题】按ABCD的顺序入栈，求所有出栈的可能
【答案】

//A在第一个位置的情况
ABCD
ABDC
ACBD
ACDB
ADCB
//A在最后一个位置的情况
BCDA
BDCA
CBDA
CDBA
DCBA
//A在第二个位置的情况
BACD
BADC
//A在第三个位置的情况
BCAD
CBAD

【法一】公式法

【公式】有一个公式，叫卡塔兰数：#card=math&code=Cn%20%3D%20C%5E%7Bn%7D%7B2n%7D%2F%28n%2B1%29&id=T10Vt)
即n个元素入栈，共有#card=math&code=C%5E%7Bn%7D_%7B2n%7D%2F%28n%2B1%29&id=anD8j)种可能

【扩展】n个元素的二叉树，也共有#card=math&code=C%5E%7Bn%7D_%7B2n%7D%2F%28n%2B1%29&id=a93Tt)种可能
是的，两者有对应关系。二叉树的递归遍历要用到系统栈。其实在二叉树的遍历序列中，先序遍历即为各个节点在入栈时的顺序，中序遍历序列即为各节点在出栈时的顺序

[例子] 当节点入栈序列为1、2、3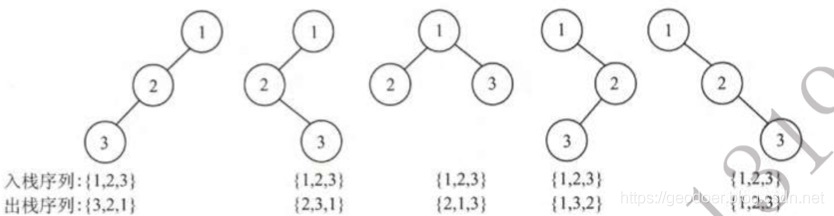

【法二】划分成子问题，求出通式

1. 1个元素进栈，有1种出栈顺序：f(1)=1
2. 2个元素进栈，有2种出栈顺序：f(2)=2
3. 3个元素进栈，有5种出栈顺序：f(3)=5

【接下来，考虑4个元素进栈】4个元素ABCD，一共有4个位置

1. A在第一个位置
   那么只可能A进栈，然后马上出栈
   此时还剩BCD等待操作，这就是子问题f(3)
   【此情况】的种数=f(3)=5
2. A在第二个位置
   那么第一个位置只能是B
   此时还剩下CD，即f(2)
   【此情况】的种数=f(1)*f(2)=2
3. A在第三个位置
   第1、2个位置只能是B、C，即f(2)
   第4个位置只能是D，即f(1)
   【此情况】的种数=f(1)*f(2)=2
4. A在第四个位置
   那么A一定是最后一个出栈
   此时还剩下BCD，即f(3)=5

【综上】4个元素按顺序入栈，总数=5+2+2+5=14个
【归纳】f(n)=f(0)*f(n-1)+f(1)*f(n-2)+...+f(n-1)*f(0)

【法三】得到全排列后筛选

【根据栈的原理】吃东西，先吃的后吐，后吃的先吐—>你已经吐出了4—>那么此时123肯定在肚子里—>123吐出来的时候，肯定是按3、2、1的顺序出现
【即】如果4出栈了，比4小的元素(1、2、3)，必须按从大到小的顺序出栈3、2、1
【筛选条件】任意的三个下标，则这种情况不存在！（即出栈顺序：3、1、2不存在）

#include<stdio.h>
#include<string.h>

void swap(char *a, char *b) {
    char tmp = *a;
    *a = *b;
    *b = tmp;
}

int cnt; //总数
void perm(char a[], int l, int r) {
    int x,y,z;
    int i,tmp;
    if (l==r) {
        // 删除不是栈的情况
        for (x=0; x<=r-2; x++) { //第一个
            for (y=x+1; y<=r-1; y++) { //第二个
                for (z=y+1; z<=r; z++) { //第三个
                    if ( a[y]<a[z] && a[z]<a[x] ) //即3、1、2的时候
                        return ; 
                }
            }
        }

        cnt++;
        printf("%s\n", a);
    } else {
        // a[l]这个位置有多种可能，a[l]-a[r]的元素都可能在这个位置
        for (i=l; i<=r; i++) {
            swap(&a[i], &a[l]);
            perm(a, l+1, r);
            swap(&a[i], &a[l]);
        }
    }
}
int main() {
    char order[30];
    scanf("%s", order);
    cnt=0;

    printf("\n");
    perm(order, 0, strlen(order)-1);
    printf("总数：%d\n", cnt);

    return 0;
}

【法四】模拟栈得出所有结果

按ABCD顺序入栈，有这样的思路

1. A入栈：这时候A是出栈，还是留着呢？
   1. B入栈：这时候B是出栈，还是留着呢？
      1. C入栈：这时候C是出栈，还是留着呢？
         1. D入栈：这时候D出栈，还是留着呢？

所以，按顺序入栈时，每个元素都有两种情况，是入栈？还是出栈？

//输入压栈顺序如1 2 3 4 5 6 7 8 ..n，确定所有可能出栈的得到的结果
//同时计算情况的总数n
#include <stdio.h>
#include <iostream>
#include <stack>
#include <queue>

using namespace std;
//递归法只计算所有情况总数
int getPermuStack(int n, int m)
{
     if(n == 0)//递归边界
     return 1;
     if(m == 0)//(n,0)问题的处理
     return getPermuStack(n-1, 1);
     return getPermuStack(n, m-1) + getPermuStack(n-1, m+1);
}
//下面算法函数既输出所有可能压栈（不全压，但仍按给定顺序压栈）的情况，也输出对应的出栈情况及总数
int n,i,j;
int res;
stack <int> s;
queue <int> in,out;
void clear(stack <int> &s)
{
    while(!s.empty())
    s.pop();
}
void clear(queue <int> &s)
{
    while(!s.empty())
    s.pop();
}
void print(queue <int> i)
{
    while(!i.empty())
   {
    cout<<i.front();
    i.pop();
   }
    cout<<endl;
}
void dostack(queue <int> in,stack <int> s,queue <int> out)
{
    if(in.empty())
     {
        if(s.empty())
       {
          res++;
          print(out);
       }
       else
       {
          out.push(s.top());
          s.pop();
          dostack(in,s,out);
       }
    }
    else
    {
       if(!s.empty())
        {
         stack <int> ts;
         queue <int> tin,tout;
         tin=in;
         ts=s;
         tout=out;
         tout.push(ts.top());
         ts.pop();
         dostack(tin,ts,tout);
        }
         s.push(in.front());
         in.pop();
         dostack(in,s,out);
    }
}
int main()
{
      cout<<"请输入1~n共n个数:";
      while(cin>>n)
      {
        res=0;
        clear(in);
        clear(out);
        clear(s);
        for(i=n;i>=1;i--)
              in.push(i);
        dostack(in,s,out);
        cout<<"对应的出栈情况总数="<<res<<endl;

      }
      cout<<"1~n依次进栈时，使用递归函数所有的情况总数:"<<endl;
      for(i=1;i<15;i++)
         cout<<"n="<<i<<"  "<<getPermuStack(i,0)<<endl;

      return 0;
}

拓展

全排列

#include<stdio.h>
#include<string.h>
void swap(char *a, char *b) {
    char tmp;
    tmp = *a;
    *a = *b;
    *b= tmp;
}
void permutation(char* str,int sbegin,int send)    //全排列的非去重递归算法  
{  
    int i;
    if(sbegin == send) //当 sbegin = send时输出  
    {  
        for( i = 0; i<=send; i++)   //输出一个排列  
            printf("%c", str[i]);
        printf("\n");
    }  
    else  
    {  
        for( i = sbegin; i <= send; i++) //循环实现交换和sbegin + 1之后的全排列  
        {  
            swap(&str[i], &str[sbegin]);   //把第i个和第sbegin进行交换
            permutation(str, sbegin + 1, send);  
            swap(&str[i], &str[sbegin]);   //【注1】交换回来  
        }  
    }  
}

int main() {
    char tmp[50];
    scanf("%s", tmp);

    printf("全排列：\n");
    permutation(tmp, 0, strlen(tmp)-1);

}

思路解析：https://blog.csdn.net/summerxiachen/article/details/60579623
全排列的系列问题：https://blog.csdn.net/jacky_chenjp/article/details/66477538

模拟入栈出栈判断序列是否正确

#include<stdio.h>

int main() {
    int inorder[] = {1,2,3,4,5}; //入栈顺序
    int outorder[] = {2,1,5,3,4}; //待检测的出栈顺序

    int stack[50];int top=-1; //栈
    int i,j;

    j=0; //遍历出栈顺序outorder
    for (i=0; i<5; i++) { //循环inorder
        stack[++top]=inorder[i]; //模拟入栈
        if (stack[top]!=outorder[j]) //当前栈顶不是和j相同
            continue; //跳出后面的语句，继续模拟入栈
        //入栈直到栈顶元素和outorder相同
        while (top!=-1) { //栈不为空
            if (stack[top]==outorder[j]) { //栈顶和outorder的元素相同
                j++; //表示当前序列这个位置是正确的
                top--; //出栈
            } else 
                break;
        } //栈空就继续下去
    }
    if (top!=-1) { //栈还有东西
        printf("错误");
    } else //栈没有东西
        printf("正确");

    return 0;
}