题目来源:严蔚敏《数据结构》C语言版本习题册 6.75、6.76
【题目】6.75
试写以递归算法,由6.73题定义的广义表表示法的字符序列,构造树的孩子链表。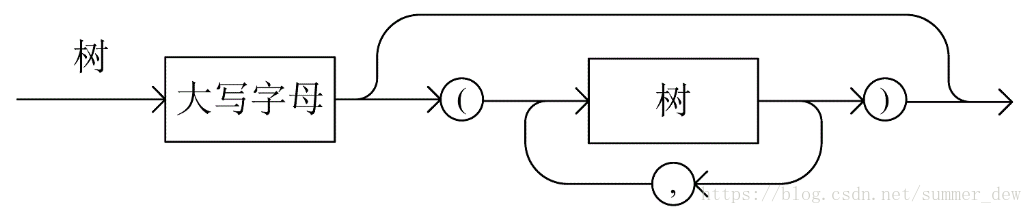
【题目】6.76
试写以递归算法,以6.73题给定的树的广义表表示法的字符序列形式输出以孩子链表表示的树。
【测试数据】A(B(E,F),C(G),D)
【答案】
/*-------------------------|6.75 用广义表构造树 |-------------------------*/// @Quesion:有一些格式检测不了"A(" "A()" "A)("Status CreateCTreeByGList(CTree *pT, int parent) {// 创建新结点newNode --> 放在下标为pT->n// 该结点的爸爸为parentchar c;CNode *p, *q;int newNode;//创建newNode结点newNode = pT->n; //新结点的下标for (c=getchar(); c!='\n'; c=getchar() ) {if (c>='A' && c<='Z') { // 结点信息pT->nodes[newNode].data = c; //给结点赋值pT->nodes[newNode].firstchild = NULL; //给结点赋值pT->n++; //结点数+1//newNode有爸爸,即parentif (parent!=-1) {//创建孩子结点p = (CNode *)malloc(sizeof(CNode));if (!p) exit(OVERFLOW);p->index = newNode;p->next = NULL;//儿子父亲相认if (pT->nodes[parent].firstchild==NULL) {pT->nodes[parent].firstchild = p;} else {for (q=pT->nodes[parent].firstchild; q->next; q=q->next) ;q->next = p;}}} else if (c=='(') { //是newNode的孩子CreateCTreeByGList(pT, newNode); //开始创建newNode的孩子} else if (c==',') { //是newNode的兄弟,即parent的下一个孩子CreateCTreeByGList(pT, parent); //parent的下一个孩子return OK; //newNode结点构造完成(自己创建了、孩子创建了、兄弟创建了)} else if (c==')') { //parent构造完毕return OK;} else {return ERROR; //格式错误}}return OK;}/*-------------------------|6.76 以广义表的形式输出 |-------------------------*/Status PrintAsGList(CTree T,int parent) {CNode *p;if (T.n<=0) return ERROR;visit(T.nodes[parent].data);if (T.nodes[parent].firstchild) {printf("(");for (p=T.nodes[parent].firstchild; p; p=p->next) {PrintAsGList(T, p->index);if (p->next) printf(",");}printf(")");}return OK;}
【完整代码】
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#ifndef BASE
#define BASE
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW -2
typedef int Status;
typedef int bool;
#endif
#define TElemType char
void visit(TElemType e) {
printf("%c", e);
}
#define MAX_TREE_SIZE 100
#define maxSize 50
typedef struct CNode{
int index; //这个孩子的结点号(注意:在严书中变量名为child)
struct CNode *next; //下一个孩子结点
}CNode, *ChildPtr; //孩子结点结构(在严书中名为CTNode)
typedef struct{
TElemType data;
CNode* firstchild;
}PNode; //双亲结点结构(在严书中,结构名为CTBox)
typedef struct{
PNode nodes[MAX_TREE_SIZE];
int n,r; //结点数 和 根结点的位置
}CTree; //树结构
// 先根遍历
void SubPreOrder(CTree T, int index) {
CNode *child;
visit(T.nodes[index].data);
for (child=T.nodes[index].firstchild; child; child=child->next)
SubPreOrder(T, child->index);
}
void PreOrder(CTree T) {
SubPreOrder(T, T.r);
}
/*-------------------------
|6.63 求树的深度 |
-------------------------*/
int SubTreeDepth(CTree T, int index) { //序号为index的子树深度
int max=-1; //孩子的最大深度
int sd; //孩子的深度
CNode *p;
if (!T.nodes[index].firstchild) return 1; //没有孩子,深度为1
for (p=T.nodes[index].firstchild; p; p=p->next) { //遍历该结点的所有孩子
sd = SubTreeDepth(T, p->index); //求孩子的深度
if (max<sd) max=sd;
}
return max+1; //孩子的最大深度+1
}
int TreeDepth(CTree T) {
return SubTreeDepth(T, T.r);
}
/*-------------------------
|6.72 将树打印成树状 |
-------------------------*/
void PrintAsTree(CTree T, int index, int i) {
/*思路
1. 观察题目输出的序列ABEFCGD
2. 此为树的先根遍历–>对应为二叉树存储的先序遍历
3. 前面的空格是该结点所在的层数
*/
CNode *p;
int cnt;
//输出空格
for (cnt=1; cnt<i; cnt++) printf(" ");
//输出元素
visit(T.nodes[index].data);printf("\n");
//遍历它的孩子
for(p=T.nodes[index].firstchild; p; p=p->next)
PrintAsTree(T, p->index, i+1);
}
// 树的层序次序+每个结点的度 --> 创建CTree
Status CreateCTreeByLevelDegree(CTree *pT,char *levelstr, int *degree) {
CNode *c,*sibling;
int parent;
int i,cnt;
//创建结点
for (i=0; i<strlen(levelstr); ++i) {
//赋值
pT->nodes[i].data = levelstr[i];
pT->nodes[i].firstchild = NULL;
}
pT->n=strlen(levelstr); //个数
pT->r=0; //根结点
//为孩子找爸爸
parent=0; //当前的爸爸
i=1; //遍历孩子
cnt=0; //已经为parent找到了cnt个孩子
while (i<strlen(levelstr)) {
if (degree[parent]==0 || cnt==degree[parent]) { //parent没有孩子 || parent的孩子已经全部找到
cnt=0;
parent++;
continue;
}
cnt++; //为parent找到了一个孩子
//创建孩子结点
c = (CNode *)malloc(sizeof(CNode)); if (!c) exit(OVERFLOW);
c->index = i; //孩子的编号
c->next = NULL;
if (cnt==1) { //第一个孩子
pT->nodes[parent].firstchild = c;
} else { //不是第一个孩子
for(sibling=pT->nodes[parent].firstchild; sibling->next; sibling=sibling->next) ;
sibling->next = c;
}
i++;
}
return TRUE;
}
/*-------------------------
|6.75 用广义表构造树 |
-------------------------*/
// @Quesion:有一些格式检测不了"A(" "A()" "A)("
Status CreateCTreeByGList(CTree *pT, int parent) {
// 创建新结点newNode --> 放在下标为pT->n
// 该结点的爸爸为parent
char c;
CNode *p, *q;
int newNode;
//创建newNode结点
newNode = pT->n; //新结点的下标
for (c=getchar(); c!='\n'; c=getchar() ) {
if (c>='A' && c<='Z') { // 结点信息
pT->nodes[newNode].data = c; //给结点赋值
pT->nodes[newNode].firstchild = NULL; //给结点赋值
pT->n++; //结点数+1
//newNode有爸爸,即parent
if (parent!=-1) {
//创建孩子结点
p = (CNode *)malloc(sizeof(CNode));if (!p) exit(OVERFLOW);
p->index = newNode;
p->next = NULL;
//儿子父亲相认
if (pT->nodes[parent].firstchild==NULL) {
pT->nodes[parent].firstchild = p;
} else {
for (q=pT->nodes[parent].firstchild; q->next; q=q->next) ;
q->next = p;
}
}
} else if (c=='(') { //是newNode的孩子
CreateCTreeByGList(pT, newNode); //开始创建newNode的孩子
} else if (c==',') { //是newNode的兄弟,即parent的下一个孩子
CreateCTreeByGList(pT, parent); //parent的下一个孩子
return OK; //newNode结点构造完成(自己创建了、孩子创建了、兄弟创建了)
} else if (c==')') { //parent构造完毕
return OK;
} else {
return ERROR; //格式错误
}
}
return OK;
}
/*-------------------------
|6.76 以广义表的形式输出 |
-------------------------*/
Status PrintAsGList(CTree T,int parent) {
CNode *p;
if (T.n<=0) return ERROR;
visit(T.nodes[parent].data);
if (T.nodes[parent].firstchild) {
printf("(");
for (p=T.nodes[parent].firstchild; p; p=p->next) {
PrintAsGList(T, p->index);
if (p->next) printf(",");
}
printf(")");
}
return OK;
}
int main() {
/*6.75测试数据
A(B(E,F),C(G),D)
A
A(B)
A(B,C)
A(B,C(D,E))
*/
CTree T;
T.n=0;T.r=0;
CreateCTreeByGList(&T, -1); //6.75
PrintAsGList(T, T.r); //6.76
return 0;
}

